235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

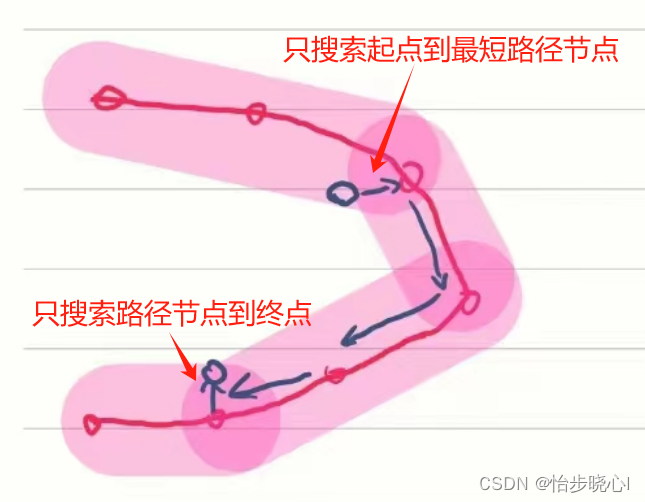
思路:上一篇文章有普通二叉树求最近公共祖先的讲解,本题也同样适用这个方法,但是我们可以利用二叉搜索树的特点,进一步优化代码,在二叉搜索树中公共祖先的val值一定介于两目标结点的val值之间(包括等于其中的一个值) .从上往下遍历这颗二叉搜索树,第一个遇到的val值介于pq的val值之间的结点一定是他们的公共结点.为什么?从该结点往左遍历,那么以后遇到的结点一定不是q的祖先结点,往右遍历,以后遇到的结点一定不是p的祖先结点.

递归三部曲:

1.确定返回值和参数的类型

返回目标结点,传入要遍历的树,和需要寻找的结点

TreeNode  traversal(TreeNode cur, TreeNode p, TreeNode q)

2. 确定结束条件

if (cur == NULL) return cur;

3.确定单层递归逻辑

根据二叉搜索树的特点,搜索二叉树,从上往下搜索到的第一个结点的val介于(包括等于其中的一个值)

 if(cur.val>p.val&&cur.val>q.val){
            return travel(cur.left,p,q);
        }

 if(cur.val<p.val&&cur.val<q.val){
            return travel(cur.right,p,q);
        }

return cur;

代码参考:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return travel(root,p,q);
    }
    public TreeNode travel(TreeNode cur,TreeNode p,TreeNode q){
        
        //
        if(cur.val>p.val&&cur.val>q.val){
            return travel(cur.left,p,q);
        }
        if(cur.val<p.val&&cur.val<q.val){
            return travel(cur.right,p,q);
        }
        return cur;
    }
}

---

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]

思路:只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。

递归三部曲:

1.确定返回值和参数类型

返回一颗插入 结点后的树,传送需要插入的树,和需要插入的数

2.确定结束条件

遇到空结点就插入

3.确定单层逻辑

与当前结点的val值比较后决定插入在哪颗子树中

if(root.val<val) root.right= insertIntoBST(root.right,val);
    if(root.val>val) root.left=insertIntoBST(root.left,val);

代码参考:

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
    if(root==null) return new TreeNode(val);
    if(root.val<val) root.right= insertIntoBST(root.right,val);
    if(root.val>val) root.left=insertIntoBST(root.left,val);
    return root;
    }
   
}

 

---

450.删除二叉搜索树中的结点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

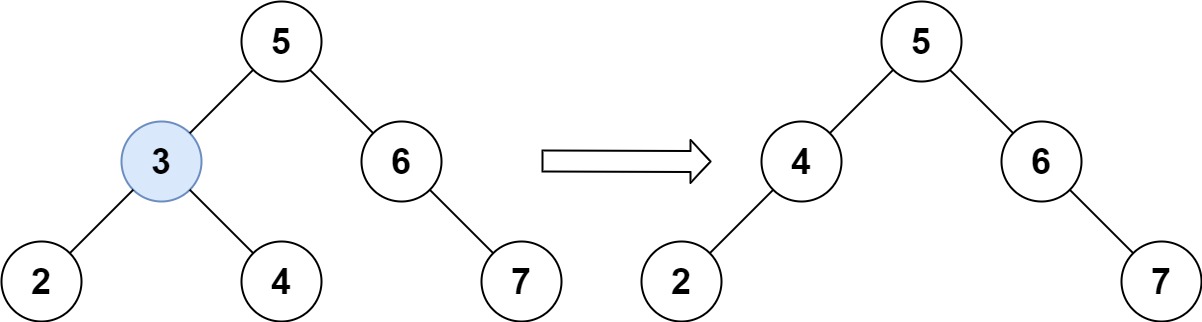
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]

思路:二叉搜索树的删除比添加难,需要改变树的结构.

将删除的结点的情况分为以下五种:

1.没找到删除的节点，遍历到空节点直接返回

找到删除的节点

2.左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点

3.删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

4.删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

5.左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

递归三部曲:

1.确定返回值和参数的类型:

返回一颗被修改的树,传入要修改的树和要删除的结点

2.确定结束条件:

删除结点的五种情况

3.单层递归逻辑

根据当前结点的val值决定在哪颗子树中删除

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
    if(root==null) return null;
    if(root.val==key&&root.left==null) return root.right;
    if(root.val==key&&root.right==null) return root.left;
    if(root.val==key&&root.left!=null&&root.right!=null){
        TreeNode cur=root.right;
//找到右子树的最左结点
        while(cur.left!=null){
            cur=cur.left;
        } 
//最左结点的左子树改为root的左子树
        cur.left=root.left;
        root.left=null;
        return root.right;//返回删除结点后的新树
    }
    if(root.val!=key){
        if(root.val>key){ root.left=deleteNode(root.left,key);}
        else{
root.right=deleteNode(root.right,key);
        }
        
    }
    return root;
    }
}