主页:醋溜马桶圈-CSDN博客
专栏:C语言_醋溜马桶圈的博客-CSDN博客
gitee:mnxcc (mnxcc) - Gitee.com
目录
1.三目运算符的使用
三目运算符,即a>b?a:b类型的,很多时候适当的使用三目运算符可以使得代码更简洁有序,减小代码的复杂程度,接下来的例子就可以很明显的展示三目运算符的作用
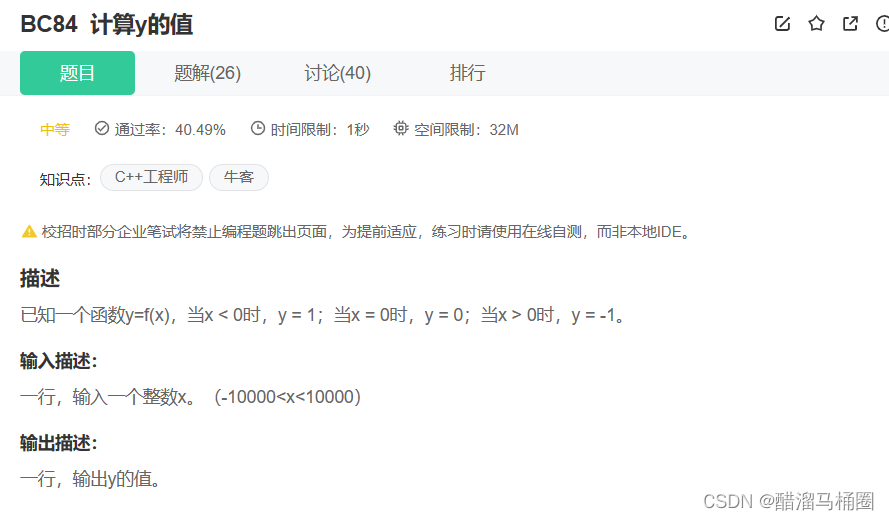
1.1 if-else语句
使用if-else语句来编写代码,如下
#include <stdio.h>
int main()
{
int x=0;
int y;
scanf("%d",&x);
if(x<0){
y=1;
printf("%d",y);
}
else if (x==0) {
y=0;
printf("%d",y);
}
else {
y=-1;
printf("%d",y);
}
}1.2 三目运算符
#include <stdio.h>
int main()
{
int x,y;
scanf("%d",&x);
x>0?(y=-1):(x==0?(y=0):(y=1));
printf("%d",y);
}三条if语句即用一条代码代替了,这也是之前文章中提到的编程思维的体现,作为程序员,写程序不是为了简单的运行成功,而是要条理清晰的写出代码,让每一步的运行都有据可循,这样也能减少代码的出错率
2.求两个正整数的最小公倍数
2.1 题目描述

牛客网中的题目描述是这样的
题目链接:求最小公倍数__牛客网
2.2 题目分析
假设两个正整数a,b;
- 最小公倍数,最小也是这两个数中的较大的一个
思路
我们可以定义一个变量,变量从这个较大的值开始,看能不能整除这两个数,如果不行,那就+1继续判断,如果不行就继续+1判断,直到可以整除这两个数,则返回最后这个数

2.3 代码(头脑风暴)
2.3.1 代码1
#include <stdio.h>
int main() {
long a=0;
long b=0;
scanf("%ld %ld",&a,&b);
long max=a>b?a:b;
while(max%a!=0||max%b!=0){
max++;
}
printf("%ld",max);
return 0;
}顺着这样的逻辑,我们可以写出这样的代码,看似没有问题,但是当遇到非常大的数字的时候,这个算法就显得很复杂,并不能在规定时间内运行,就像这样

究其原因,是因为我们一个一个试数字,这样的方法其实是最耗费时间的;
那有没有更快的算法呢?答案是肯定的
2.3.2 代码2
我们假设存在一个数字m,同时能整除a和b;假设m/a=i,m/b=j;
i的取值肯定是从1开始的,假设我们得到一个i值,这个i*a能整除b,那就说明i*a就是最小公倍数

我们发现,在代码1的逻辑中,我们求最小公倍数用了10次循环; 在这个算法中,我们只用了5次循环便找出了最小公倍数,速度提升了很多
那么我们就顺着这个逻辑写我们的代码2
#include <stdio.h>
int main() {
long a=0;
long b=0;
scanf("%ld %ld",&a,&b);
long i=1;
while(1){
if((i*a)%b==0){
break;
}
i++;
}
printf("%ld",i*a);
return 0;
}这个时候我们发现,代码顺利通过了
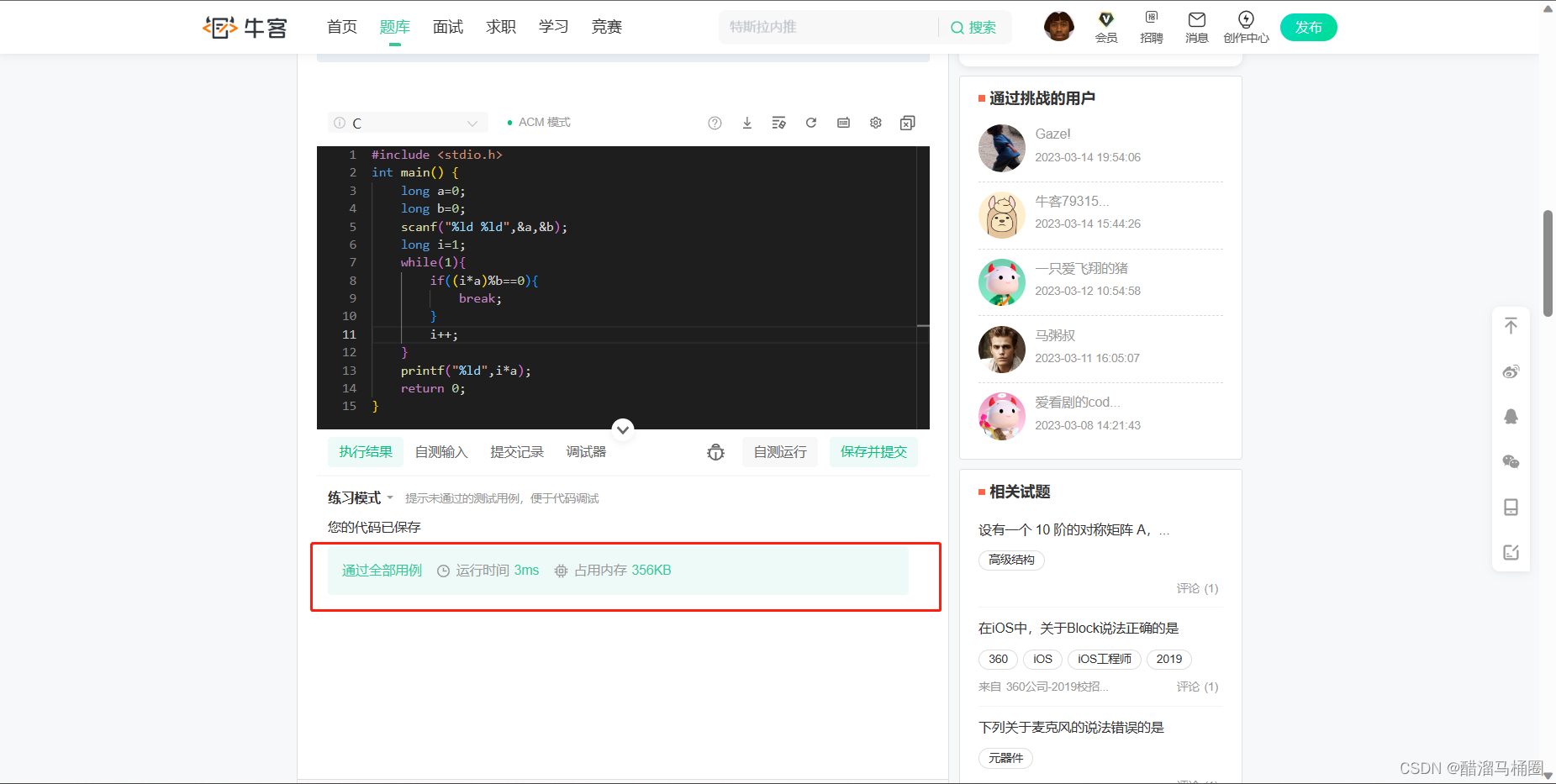
可见我们这个逻辑是行得通的,至此,我们的最小公倍数问题就求解成功了
2.3.3 思考:为什么要用long?
我们发现,题目的输入描述范围是1-100000
而int的表示范围有限,我们通过实践发现,用int型并不能很好的实现


3.倒置字符串
3.1 题目描述
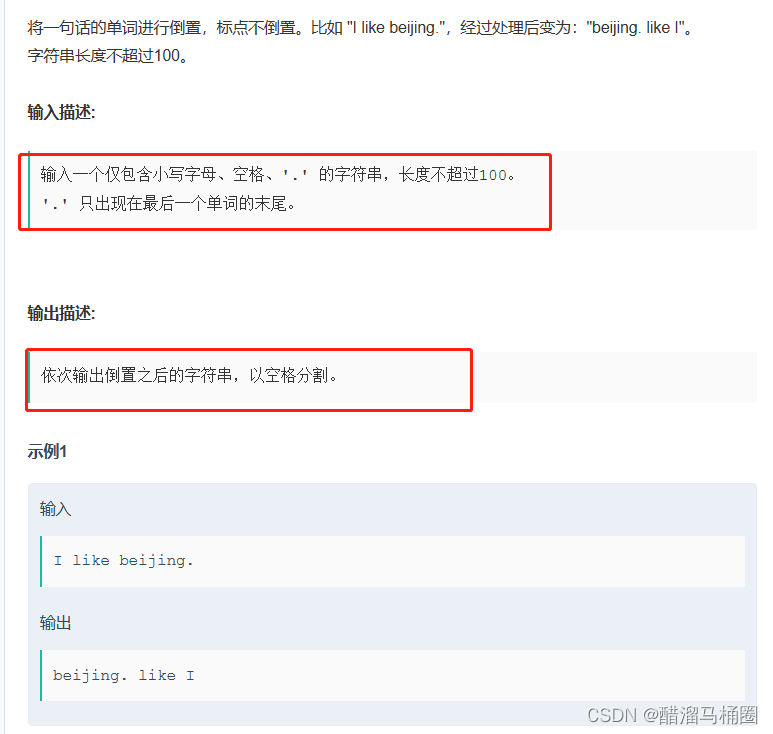
题目链接:倒置字符串__牛客网
3.2 题目分析
思考一下,我们可以分为两步
- 第一步,将整个字符串逆序
- 第二步,把逆序后的每个单词再逆序
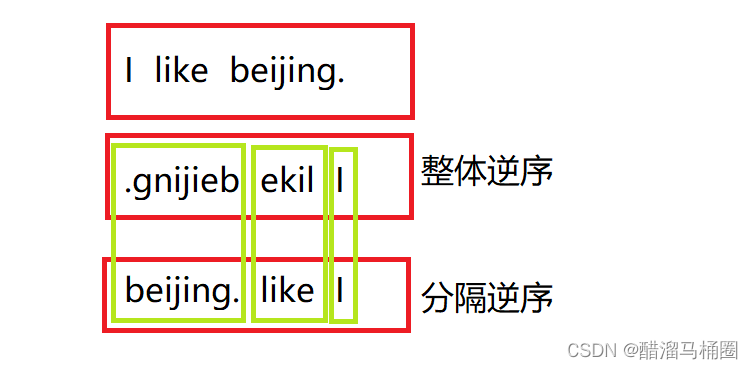
或者我们可以:
- 第一步,逆序每个单词
- 第二步,再逆序整个字符串
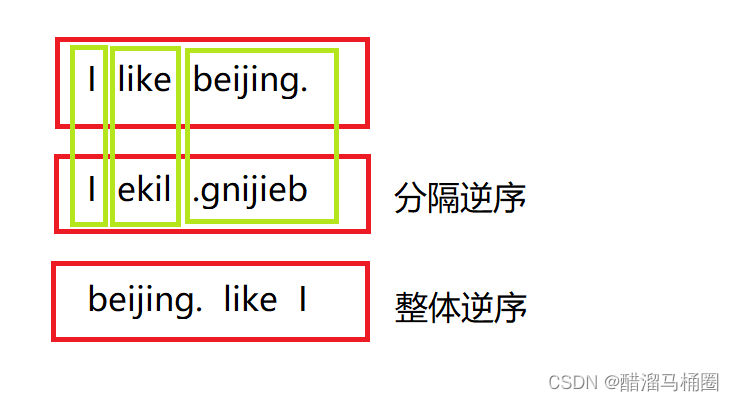
- 逆序字符串,需要告诉字符串的起始位置和结束位置
- 逆序单词,同样需要告诉单词的起始位置和结束位置
这两种算法思维都是可以的,那我们实践一下
3.3 代码
我们可以封装一个reverse函数来进行字符串逆序
实现逻辑是这样的
3.3.1 reverse函数

void reverse(char* left,char* right){
while (left<right) {
char tmp=*left;
*left=*right;
*right=tmp;
left++;
right--;
}
}逆序整个字符串,调用这个函数,逆序单词同样可以调用这个函数
用while循环,当开始指针遇到空格或者'\0'的时候就停止;没有遇到空格或者'\0'的时候,则是一个单词,逆序这个单词
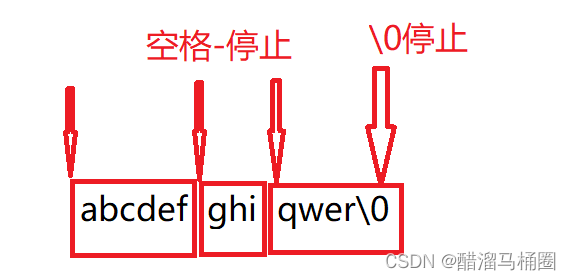
可以看主函数的代码理解
3.3.2 主函数
#include <stdio.h>
void reverse(char* left,char* right){
while (left<right) {
char tmp=*left;
*left=*right;
*right=tmp;
left++;
right--;
}
}
int main() {
char arr[101]={0};
gets(arr);
//逆序整个字符串
int len=strlen(arr);
reverse(arr,arr+len-1);
//逆序每个单词
char* cur=arr;
while(*cur){
char* strat=cur;
while (*cur!=' '&&*cur!='\0') {
cur++;
}
char* end=cur-1;
reverse(strat, end);
if(*cur==' ')
cur++;
}
printf("%s\n",arr);
return 0;
}这样,我们这个问题就解决了

3.3.3 为什么使用gets()接收字符串呢?
因为scanf()接收字符串,遇到空格就停止不会继续往后读取了

4.二维数组中的查找
二维数组中的查找,这是剑指offer中的一道数组方面的题目
牛客网中也有同样的题目
4.1 题目描述

4.2 题目分析
我们在把这个二维数组用图表示出来
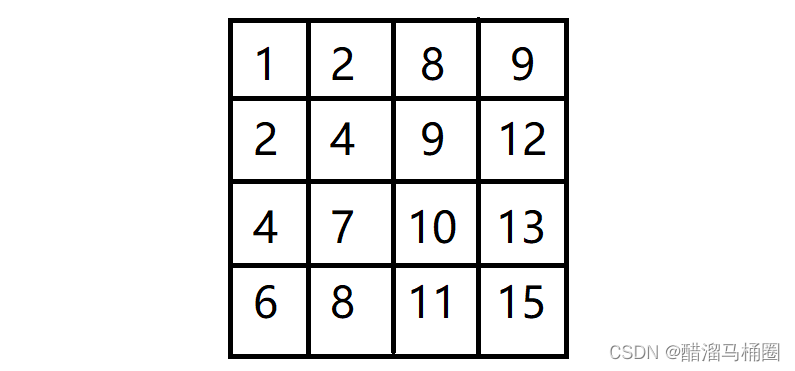
4.2.1 二维数组中数字7的查找
由题目可知,每一行的数字是从左向右增大的,每一列的数字是从上到下增大的,即
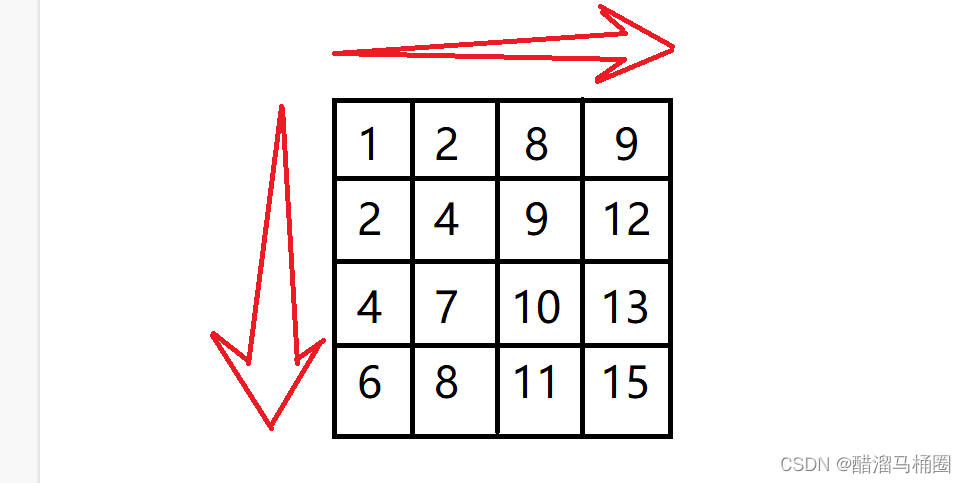
首先,我们选取数组右上角的数字9,由于9大于7,并且9是第四列第一个(也是最小的)数字,因此7不可能出现在数字9所在的列。于是,我们把这一列从需要考虑的区域内剔除,之后只需要分析剩下的3列。
在剩下的矩阵中,位于右上角的数字是8,同样8大于7,因此8所在的列我们也可以剔除。接下来我们只要分析剩下的两列即可。
在剩余两列组成的数组中,数字2位于数组的右上角。2小于7,那么要查找的7就可能出现在2的右边和下边,而在前两步中,我们已经排除了2右边的列,也就是说7不可能出现在2的右边,只有可能出现在7的下边。于是我们把2所在的行也剔除,只分析剩下的三行两列数字。
在剩下的数字中,数字4位于右上角,和前面一样,我们把数字4所在的行也剔除,最后只剩下两行两列数字。
在剩下的两行两列中,位于右上角的数字刚好就是我们要查找的数字7,于是查找过程结束。
用下图表示

4.2.2 二维数组中数字的查找规律
首先选取数组中右上角的数字。如果该数字等于要查找的数字,则查找过程结束;
如果该数字大于要查找的数字,则剔除这个数字所在的列;如果该数字小于要查找的数字,则剔除这个数字所在的行。
也就是说,如果要查找的数字不在数组的右上角,则每一次都在数组的查找范围中剔除一行或者一列,这样每一步都可以缩小查找的范围,直到找到要查找的数字,或者查找范围为空。
4.3 代码示例
把整个查找过程分析清楚之后,我们再写代码就不是一件很难的事情了。
下面是关于该思路的代码:
bool Find(int target, int** array, int arrayRowLen, int* arrayColLen) {
int iRow = 0;
int iCol = 0;
char bIsFind = false;
if (NULL == array)
return false;
iRow = 0;
iCol = *arrayColLen - 1;
while (iCol >= 0 && iRow < arrayRowLen) {
if (target == array[iRow][iCol]) {
bIsFind = true;
break;
}
else if (target <= array[iRow][iCol]) {
iCol--;
}
else {
iRow++;
}
}
return bIsFind;
}5.数字在升序数组中出现的次数
这道题可以用遍历数组和二分查找来处理
5.1 题目描述

5.2 题目分析
题目中有一个关键信息,非降序数组,我们可以使用if语句来处理这个问题
if(numsLen==0){
return 0;
}
else if (nums[numsLen-1]<k||nums[0]>k) {
return 0;
}5.2.1 遍历数组方法
int GetNumberOfK(int* nums, int numsLen, int k ) {
int count = 0;
if(numsLen==0){
return 0;
}
else if (nums[numsLen-1]<k||nums[0]>k) {
return 0;
}
for(int i=0;i<numsLen;i++){
if (k==nums[i]) {
count++;
}
}
return count;
}遍历数组的方法应该是最直接有效的,当k出现一次,则count自增,最终返回count的值即是k出现的次数
5.2.2 二分查找方法
二分查找是我们经常使用的一种算法,他的逻辑是
在升序或者降序且无重复元素的数组中,比较目标值和数组中间值的方法,每次缩小一半的搜索范围,相比遍历可以加快计算的速度

假设:目标值为下标为4的数值,给定一个大小为10的数组,我们给定他的下界left=0,上界right=numsLen-1,中间下标mid=(left+right)/2
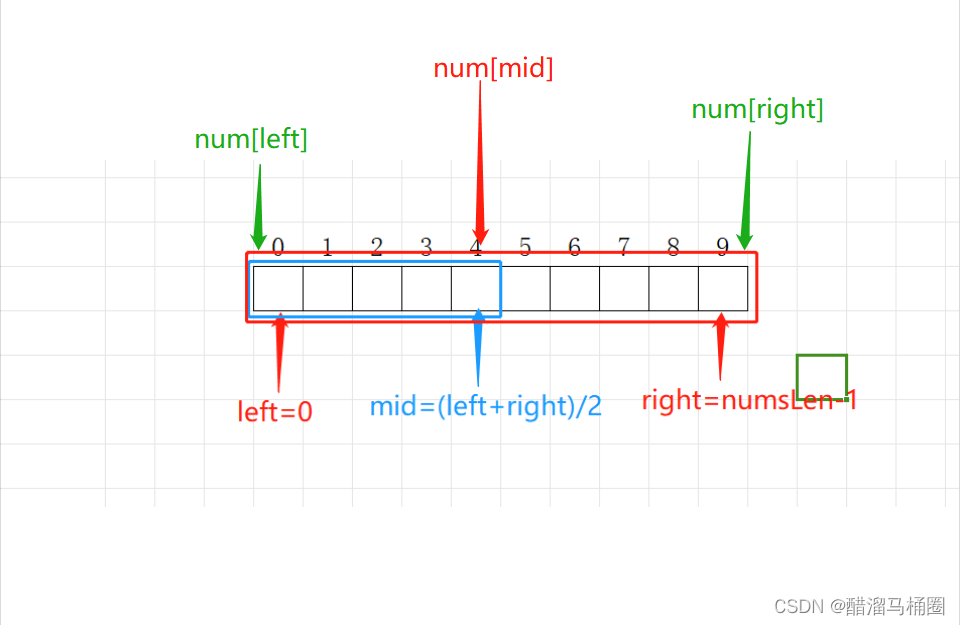
二分查找:
- 判断目标值target是否等于num[mid];
- 如果相等则返回mid
如果不相等则判断target与num[mid]的大小关系;
- target>num[mid];则说明目标值在后半部分,因为mid与目标值不相等,那么left就变成mid+1;
- target<num[mid];则说明目标值在前半部分,因为mid与目标值不相等,那么right就变成mid-1;
每次缩小范围后都需要继续执行上述步骤,我们可以使用一个while循环,当left<right的时候循环,直到找到目标值对应的下标,返回下标;或者没有目标值对应的下标,返回-1;
5.2.3 代码示例
按照这个思路,我们编写一下我们的代码
int position(int* data, int n, double k){
int left = 0, right = n-1, mid = 0;
while(left <= right){
mid = (left + right)/2;
if(data[mid] < k)
left = mid + 1;
else if(data[mid] > k)
right = mid - 1;
else
return mid;
}
return left;
}当然,这是二分查找的代码,根据题目要求,我们调用这个函数
int GetNumberOfK(int* nums, int numsLen, int k ){
return position(nums,numsLen, k+0.5) - position(nums,numsLen, k-0.5);
}找到比k小的第一个数作为左边界,找到比k大的第一个数作为右边界,右-左即k的个数
按普通找某个数的位置来找,只是把int 改为double, 找k-0.5和k+0.5
6.BM80 买卖股票的最好时机(一)
6.1 题目描述
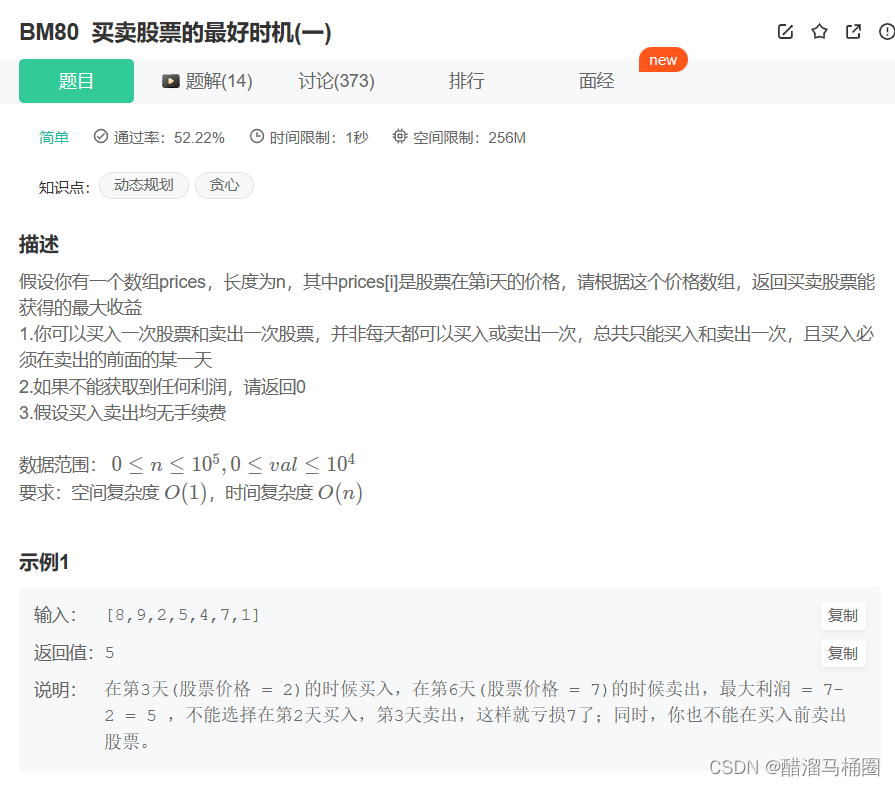
题目链接:买卖股票的最好时机(一)_牛客题霸_牛客网 (nowcoder.com)
6.2 题目分析
我们看到这个题目中一个数组表示每一天的股价,那么最大利润怎么算呢,我们用图片来表示
假设这是我们输入的数组
根据题目的意思,我们需要在股价最低的时候买入,在股价最高的时候抛出;但是这有一个问题,我们只能在买入当天以后的股价中找利润最大的,如果没有最大的,那就返回0;我们推理一下
-
第一天:最小值8 利润:8-8=0
-
第二天:最小值8 利润:9-8=1
-
第三天:最小值2 利润:2-2=0
-
第四天:最小值2 利润:4-2=2
-
第五天:最小值2 利润:10-2=8
-
第六天:最小值1 利润:1-1=0
-
......
-
依次递推即可知道:最大利润值即为8
6.3 编写代码
根据这个逻辑,写代码的时候我们需要初始化最低股价min,最大效益maxProfit,当前股价price
- 当前股价我们需要假设每一天的情况,所以我们用for循环遍历数组实现
- 最低股价我们假设数组的第一个元素是最低股价,然后与当前股价比较得出最低股价
- 每一天的最大利润是当前股价减去最低股价
- 比较每天的最大利润,得出所有最大利润中的最大利润返回
- 没有利润则返回0
我们编写出下面这段代码
int maxProfit(int* prices, int pricesLen ) {
// write code here
int min=*prices;
int maxProfit=0;//初始化最大利润
int price=0;//初始化当前股价
for(int k=0;k<pricesLen;k++){
price=prices[i];
min=min<price?min:price;//求出当前股价之前的最低股价
maxProfit=maxProfit<(price-min)?(price-min):maxProfit;
}
return maxProfit;
}
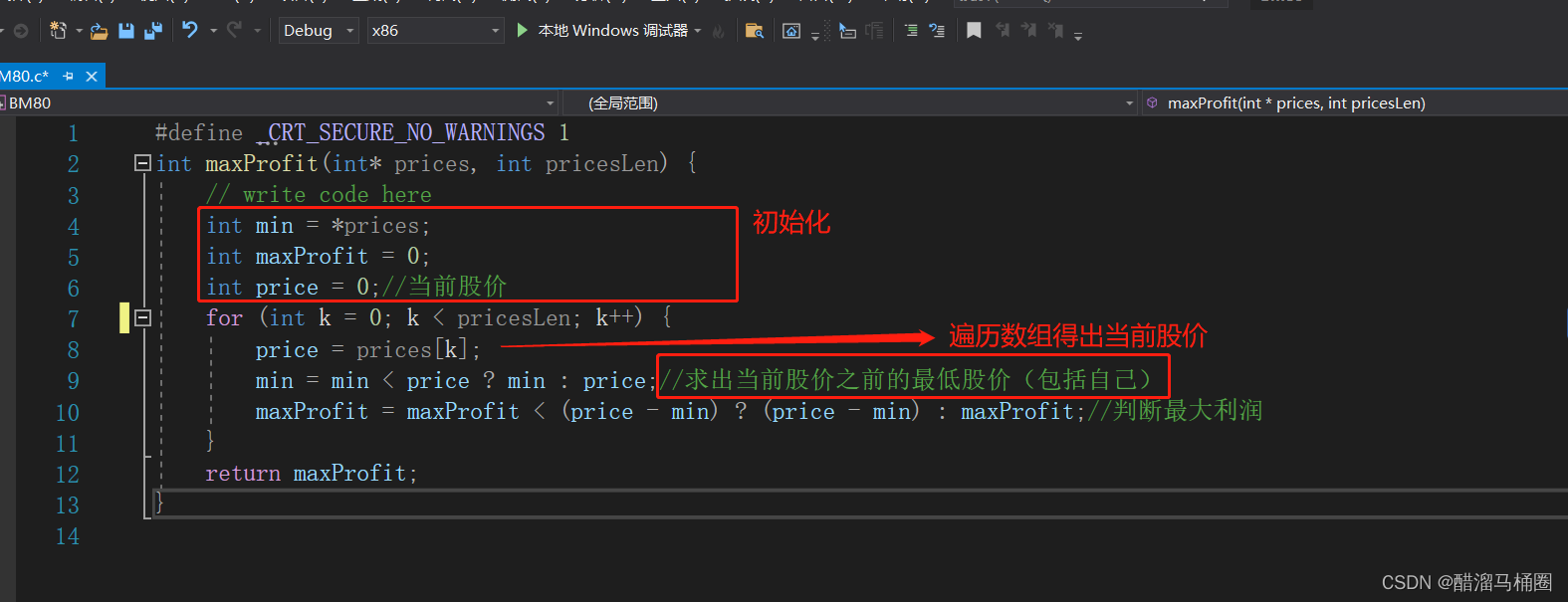
7.二分查找逻辑
7.1 二分查找
二分查找是我们经常使用的一种算法,他的逻辑是
在升序或者降序且无重复元素的数组中,比较目标值和数组中间值的方法,每次缩小一半的搜索范围,相比遍历可以加快计算的速度

7.2 查找逻辑
假设:目标值为下标为4的数值,给定一个大小为10的数组,我们给定他的下界left=0,上界right=numsLen-1,中间下标mid=(left+right)/2

判断目标值target是否等于num[mid];
- 如果相等则返回mid
如果不相等则判断target与num[mid]的大小关系;
- target>num[mid];则说明目标值在后半部分,因为mid与目标值不相等,那么left就变成mid+1;
- target<num[mid];则说明目标值在前半部分,因为mid与目标值不相等,那么right就变成mid-1;
每次缩小范围后都需要继续执行上述步骤,我们可以使用一个while循环,当left<right的时候循环,直到找到目标值对应的下标,返回下标;或者没有目标值对应的下标,返回-1;
7.3 题目练习
我们找到一个题目来练习一下
7.3.1 题目描述

牛客网的题目链接: 二分查找-I_牛客题霸_牛客网 (nowcoder.com)
7.3.2 代码示例
根据二分查找的逻辑,我们可以写下代码:
int search(int* nums, int numsLen, int target ) {
if(nums==NULL){
return -1;
}
int left=0;
int right=numsLen-1;
int mid=(left+right)/2;
while (left<=right) {
if (nums[mid]>target) {
right=mid-1;
}
else if (nums[mid]<target) {
left=mid+1;
}
else
return mid;
mid=(left+right)/2;
}
return -1;
}








![完全二叉树的层序遍历[天梯赛]](https://img-blog.csdnimg.cn/direct/ec467080d3654542ab81438ff509b88d.png)
