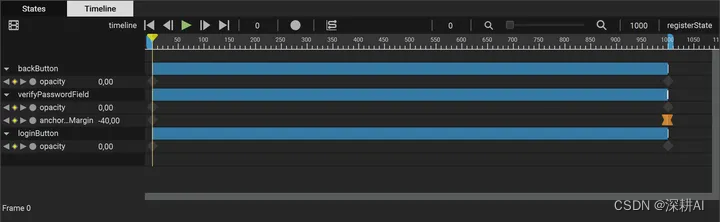
例题一

算法思路:
纯模拟。从前往后遍历整个字符串,找到问号之后,就⽤
a ~ z
的每⼀个字符去尝试替换即
可。
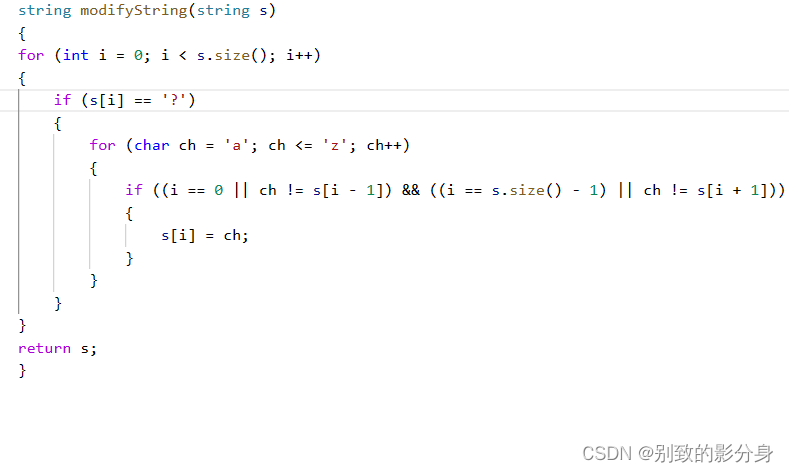
例题二

解法(模拟 + 分情况讨论):
算法思路: 模拟 + 分情况讨论。
计算相邻两个时间点的差值:
i.
如果差值⼤于等于中毒时间,说明上次中毒可以持续 duration
秒;
ii.
如果差值⼩于中毒时间,那么上次的中毒只能持续两者的差值。

例题三

解法(模拟 + 找规律):
算法思路:
找规律,⽤ row 代替⾏数,row = 4 时画出的 N 字形如下:
0 2row - 2 4row - 4
1 2row - 3 2row - 1 4row - 5 4row - 3
2 2row-4 2row 4row - 6 4row - 2
3 2row + 1 4row - 1
不难发现,数据是以 2row - 2 为⼀个周期进⾏规律变换的。将所有数替换成⽤周期来表⽰的变量:
第⼀⾏的数是:0, 2row - 2, 4row - 4;
第⼆⾏的数是:1, (2row - 2) - 1, (2row - 2) + 1, (4row - 4) - 1, (4row - 4) + 1;
第三⾏的数是:2, (2row - 2) - 2, (2row - 2) + 2, (4row - 4) - 2, (4row - 4) + 2;
第四⾏的数是:3, (2row - 2) + 3, (4row - 4) + 3。
可以观察到,第⼀⾏、第四⾏为差为 2row - 2 的等差数列;第⼆⾏、第三⾏除了第⼀个数取值为⾏数,每组下标为(2n - 1, 2n)的数围绕(2row - 2)的倍数左右取值。
以此规律,我们可以写出迭代算法。

例题四

解法(模拟):
算法思路:
所谓「外观数列」,其实只是依次统计字符串中连续且相同的字符的个数。依照题意,依次模拟即
可。
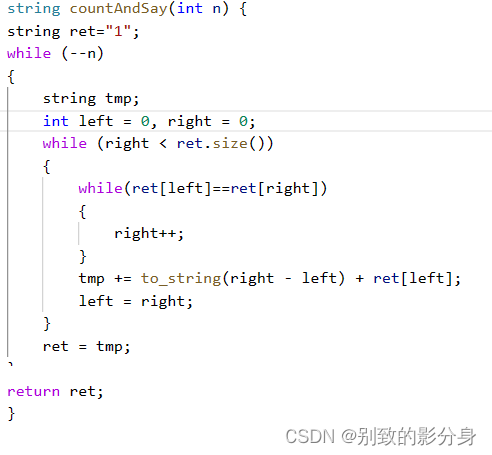
例题五

解法(模拟 + 分情况讨论)
算法思路:
模拟⻘蛙的叫声。
◦
当遇到
'r' 'o' 'a' 'k'
这四个字符的时候,我们要去看看每⼀个字符对应的前驱字符,有没有⻘蛙叫出来。如果有⻘蛙叫出来,那就让这个⻘蛙接下来喊出来这个字符;如果没有,直接返回 -1
;
◦
当遇到
'c'
这个字符的时候,我们去看看
'k'
这个字符有没有⻘蛙叫出来。如果有,就让这个⻘蛙继续去喊 'c'
这个字符;如果没有的话,就重新搞⼀个⻘蛙。