标题:【leetcode】双指针
水墨不写bug

我认为 讲清楚为什么要用双指针 比讲怎么用双指针更重要!
(一)快乐数
编写一个算法来判断一个数
n是不是快乐数。「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果
n是 快乐数 就返回true;不是,则返回false。示例 1:
输入:n = 19 输出:true 解释: 1^2 + 9^2 = 82 8^2 + 2^2 = 68 6^2 + 8^2 = 100 1^2 + 0^2 + 0^2 = 1示例 2:
输入:n = 2 输出:false提示:
1 <= n <= 2^31 - 1
题解:
记快乐数转换的对应关系为f,每一次对应关系f处理后,相当于指针向后移动一次;
由于一个数被 f 对应关系的映射后得到数的过程是不可逆转的-->【100 的得到方法不止一种:f(68) = 100;f(86) = 100, 所以知道f处理后的结果是100,但是无法确定f处理的源(原)数是谁】
根据这一特征,我们可以想象一个数据结构,它类似于单链表,由此可以联想到我们之前已经做过的问题:
链表是否成环 :链表可以仅仅是一条单链,也可以是像 “6” 一样链表,当环达到最大时,链表就成了 “0” 形。
本题 可以 类比 判断链表是否有环 的思路,但是一种情况可以忽略:一条单链表。
为什么可以忽略?
在这条“链表”中,只可能存在 “1” 或者不存在 “1” 两种情况。
如果存在“1”,由于对“1”进行 f 对应关系的映射后仍然等于 “1”,于是 “1” 单独成环;
如果不存在 “1”,对任意一个数,都可经过有限次f变换后得到它本身。
(现在证明:对任意一个数,都可经过有限次f变换后得到它本身。
int类型的范围的数量级是10^9级【10亿级】,最大的int值小于9999999999,这个值经过f变换后得到的值——9^2+9^2+9^2+9^2+9^2+9^2+9^2+9^2+9^2=729;
由于规定的输入为正整数,这意味着f的值域为[1,729],考虑到整数平方后得到的结果一定是整数,所以一个数经过最多729次变换后,它的取值取便了[1,729]的任意值,如果再进行一次f变换,得到的结果一定会与之前的值重复,命题的证。)
为什么选择双指针?
经过分析,可以知本题的数据结构是一个 “6” 形的 “链表”,正常的遍历无法得到终止,根据 链表是否成环 的经验,可以想到用快慢指针的速度差来判断,如果在“链表中存在 “1””,那么两指针会在“1”相遇;否则,两指针会在环中的一个随机位置相遇。
(具体实现f函数名称为Bitsum)
class Solution {
public:
//实现思路:取到这个数的每一位,平方后加到sum中;
int Bitsum(int n)
{
int sum = 0;
while(n)
{
int t = n%10;
sum += t*t;
n/=10;
}
return sum;
}
bool isHappy(int n) {
int slow = n,fast = Bitsum(n);
while(slow!=fast)
{
slow = Bitsum(slow);
fast = Bitsum(Bitsum(fast));
}
return slow == 1;
}
};
(二)盛水最多的容器
给定一个长度为
n的整数数组height。有n条垂线,第i条线的两个端点是(i, 0)和(i, height[i])。找出其中的两条线,使得它们与
x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
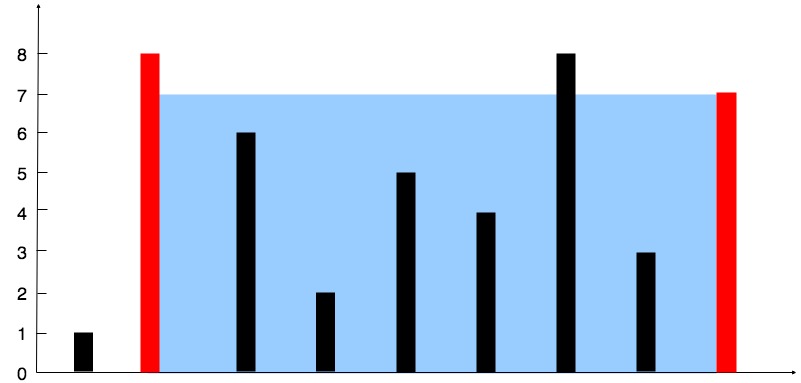
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1] 输出:1提示:
n == height.length2 <= n <= 10^50 <= height[i] <= 10^4
如果解决一道题?
首先,我会先理解这道题,通过分析示例,彻底理解题目的要求;
其次,我最先想到的是暴力求解,为什么?通过分析历年大赛的标准答案解法,最优解法往往是在暴力求解的基础上,优化暴力求解来得到的。优先考虑暴力解法,再通过优化暴力求解算法来得到更优的算法;另外,对于暴力求解算法,一些特殊测试点往往是会超时的,没有办法得到高分;
然后,分析时我发现这道题可以利用双指针来避免一些不必要的枚举结果,也就是上述的优化——优化是从多种层面的,需要一些经验积累。
最后,自己写一些测试点和结果,对照写好的程序,在纸上一步一步走读代码;这些测试点的选取要考虑全面,防止漏情况。
根据暴力求解算法,可以在数组中选择两个下标不重复的数,用较小的数 * 两数下标之差就是体积V,记录所有的V,最终返回最大的V即可;
固定一个下标(left),让另一个下标(right)向右遍历,遍历完后,left++,类推;
我们把本题抽象为桶:
既然存储最多的水,我们我们直接在遍历的过程中舍去 “短板”不就行了吗?留下最长的两个板,得到的结果V不就是最大的吗?
{
if(height[left] >= height[right])
right--;
else
left++;}
这是有人会有疑问,板长了,但是不能保证宽度大啊,V要大,前提是痛的桶壁板子和桶的内径都很大。
确实是这样的,但是不要忘了,我们还有这两句:
{
int v = min(height[left],height[right])*(right-left);
ret = max(ret,v);}
由于ret在每次变更桶壁后都会更新,并且会选择较大的V覆盖原值;
那么,就相当于在 不断增长桶壁的同时也可保存V在一系列变化中的最大值;
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0,right = height.size()-1,ret = 0;
while(left < right)
{
int v = min(height[left],height[right])*(right-left);
ret = max(ret,v);
if(height[left] >= height[right])
right--;
else
left++;
}
return ret;
}
};(三)有效三角形个数
给定一个包含非负整数的数组
nums,返回其中可以组成三角形三条边的三元组个数。示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3示例 2:
输入: nums = [4,2,3,4] 输出: 4提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
class Solution {
public:
static int my_cmp(const void*a,const void*b)
{
return *((int*)a) - *((int*)b);
}
int triangleNumber(vector<int>& nums)
{
int count = 0;
int pmax = nums.size()-1,left = 0,right = pmax - 1;
qsort(&nums[0],nums.size(),sizeof(nums[0]),my_cmp);
for(; pmax>=2 ;pmax--)
{
left = 0,right = pmax - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[pmax])
{count +=(right-left);--right;}
else {++left;}
}
}
return count;
}
};(四)总和为目标值的两个数
购物车内的商品价格按照升序记录于数组
price。请在购物车中找到两个商品的价格总和刚好是target。若存在多种情况,返回任一结果即可。示例 1:
输入:price = [3, 9, 12, 15], target = 18 输出:[3,15] 或者 [15,3]示例 2:
输入:price = [8, 21, 27, 34, 52, 66], target = 61 输出:[27,34] 或者 [34,27]提示:
1 <= price.length <= 10^51 <= price[i] <= 10^61 <= target <= 2*10^6
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0,right = price.size()-1;
while(1)
{
int sum = price[right] + price[left];
if( sum> target) right--;
else if(sum < target) left++;
else break;
}
vector<int> it = {price[left],price[right]};
return it;
}
};完~
未经作者同意禁止转载