基于matlab仿真A*算法的多目标路径规划问题

资源文件换一下剩下的看注释即可很详细的哦

% 定义地图大小   十行十列
ROWS = 10;
COLS = 10;

% % 初始化地图
% grid = zeros(ROWS, COLS);
% % 设置固定位置的障碍物
% obstacle_positions = [2, 3; 4, 5; 6, 7;]; % 障碍物位置坐标
% % 将障碍物位置设置为1
% for i = 1:size(obstacle_positions, 1)
%     grid(obstacle_positions(i, 1), obstacle_positions(i, 2)) = 1;
% end

 % 初始化地图和障碍物
 grid = zeros(ROWS, COLS);
 for i = 1:ROWS
     for j = 1:COLS
         if rand < 0.2 % 随机生成20%的障碍物
             grid(i, j) = 1;% 将单元格设置为1 表示有障碍物
         end
     end
 end

% 定义起点和终点
start = [1, 1];
end_point = [ROWS, COLS];
end_point_point = [1,10];
% 定义多个目标点
% A*算法是逐个处理目标点的，所以路径规划是按顺序进行的，而不是并行进行的。因此，两个目标点的路径规划是依次执行的，一个目标点的路径计算完成后才会开始计算另一个目标点的路径。
targets = [end_point;end_point_point];

% 实现A*算法的核心部分 在计算路径时，考虑多个目标点


% 迭代次数是指在算法中重复执行某个过程的次数。在很多算法中，特别是优化算法或者搜索算法中，通常需要通过多次迭代来逐步优化结果或者搜索空间，直至满足某个条件或者达到预设的最大迭代次数为止。
% 在路径规划算法中，比如使用启发式搜索算法或者遗传算法来寻找最优路径时，每次迭代可能会尝试探索新的路径或者调整当前路径，然后根据某种评价标准（比如路径长度或者成本）来评估路径的优劣，并更新当前的路径状态。
% 迭代次数的增加通常会使得算法有更多机会发现更优的解决方案，但也可能增加算法的计算复杂度

% 定义最大迭代次数
max_iterations = 1000;% 算法在进行路径规划最多的迭代次数

% 寻找路径
% 创建一个1行、目标点数量列的空cell数组
% 通过 size(targets, 1) 获取了 targets 矩阵的行数，即目标的数量
% 如果 targets 表示的是第十行第十列的位置，则 size(targets, 1) 将返回1，因为只有一个元素（一个位置）。因此，path 将是一个包含一个元素的单元格数组，用于存储与该目标相关的路径信息
% cell是一种特殊的数据类型，表示单元格数组。它可以用来存储不同类型和大小的数据，类似于其他编程语言中的二维数组或列表。您可以使用cell函数来创建单元格数组，也可以直接使用大括号 {} 来访问和操作单元格数组中的元素。
path = cell(1, size(targets, 1)); % 存储路径
for i = 1:size(targets, 1)% for循环遍历每一行
    iteration = 0;% 记录迭代次数 初始化操作
    % 计算起点到目标点的路径
    target_path = []; % 初始化空数组 存储单个目标点的路径
    
    % 在路径未找到且迭代次数未达到最大值时，循环执行特定操作
    % isempty() 是 MATLAB 中的一个函数，用于判断某个数组或者矩阵是否为空。
    while isempty(target_path) && iteration < max_iterations
        % A*算法核心部分
        % 定义了一个匿名函数heuristic，用于计算启发式估价函数的值
        % 启发式估价函数在A*算法中用于估计当前节点到目标节点的代价，以辅助路径搜索过程
        % 在 A* 算法的上下文中，这两个元素通常表示二维平面上的坐标。例如，如果 a 和 b 是二维平面上的两个点，则 a(1) 和 b(1) 表示这两个点的 x 坐标，a(2) 和 b(2) 表示这两个点的 y 坐标。
        % 曼哈顿距离
        heuristic = @(a, b) abs(a(1)-b(1)) + abs(a(2)-b(2));
        % 定义了一个二维数组directions，其中包含了四个方向的偏移量。每个方向偏移量是一个包含两个元素的行向量，表示在二维平面上的移动方向
        directions = [[-1, 0]; [1, 0]; [0, -1]; [0, 1]];
        % 初始化openList结构体数组，包含起点的位置、g值、h值、f值和父节点信息 :提取整行的元素
        % 这行代码初始化了一个结构体数组 `openList`，用于存储 A* 算法中待处理的节点信息。下面是对这行代码中每个字段的解释：
        % 'pos', start`：表示节点的位置，即起始位置。这个位置通常是一个二维坐标，在这段代码中使用了 `start` 变量，它可能是起始点的坐标。
        % 'g', 0`：表示节点的实际代价（也称为路径成本），在这里初始化为0。`g` 代表从起点到当前节点的实际代价。
        % 'h', heuristic(start, targets(i, :))`：表示节点到目标的估计代价，即启发式函数的值。在 A* 算法中，`h` 代表从当前节点到目标的预计代价。这里使用了启发式函数 `heuristic` 来计算当前节点到目标的曼哈顿距离。
        % 'f', 0`：表示节点的综合代价。在 A* 算法中，`f` 是一个综合考虑实际代价和估计代价的值，通常定义为 `f = g + h`。在这里，由于刚初始化节点，实际代价和估计代价都是0，所以 `f` 也初始化为0。
        %'parent', []`：表示当前节点的父节点。在 A* 算法中，每个节点都有一个指向其父节点的指针，以便在找到最佳路径时能够回溯到起点。在这里，因为是初始化节点，所以父节点为空。
        openList = struct('pos', start, 'g', 0, 'h', heuristic(start, targets(i, :)), 'f', 0, 'parent', []);
        % closedList通常用于存储已经考虑过的节点，以避免对它们进行重复处理
        closedList = [];
        
        % while ~isempty(openList)：这是一个 while 循环，它会持续执行直到 openList 变量为空。~isempty(openList) 表示当 openList 不为空时循环会继续执行。
        while ~isempty(openList)% 进入while循环，直到openList为空
            % ~ 表示要忽略的值。在 MATLAB 中，波浪线 ~ 用于指示忽略或丢弃某个值。idx 表示要获取的值。在这个例子中，idx 是变量名，用于存储从函数返回的某个值。
            [~, idx] = min([openList.f]);% 找到openList中具有最小f值的节点，并返回该节点在openList中的索引
            current = openList(idx);% 获取具有最小f值的节点
            
            % A*算法中的路径搜索和路径重建
            % isequal(current.pos, targets(i, :))：这一行代码用于检查当前节点的位置是否与目标位置相匹配。current.pos 可能是当前节点的位置，而 targets(i, :) 则表示第 i 个目标的位置。isequal 函数用于比较两个变量是否相等。
            % target_path = reconstructPath(current);：如果当前节点的位置与某个目标位置相匹配，则调用 reconstructPath 函数来重建路径。reconstructPath 函数通常是一个自定义函数，用于从当前节点向起始节点回溯，并重建完整的路径。
            % break;：一旦找到目标并重建了路径，就会跳出循环。这个循环可能是 A* 算法的主循环，也可能是一个搜索节点的循环，具体取决于整个算法的实现。

            % 搜索路径：在路径搜索问题中，我们需要找到从起点到目标点的有效路径。这通常需要使用搜索算法（比如 A* 算法）来遍历图或者网络中的节点，并找到一条满足特定条件（比如最短路径或者最低成本路径）的路径。
            % 搜索路径的目的是找到一条从起点到目标点的有效通路。重建路径：一旦找到了有效路径，我们需要将其呈现出来或者用于后续的任务。重建路径是指根据搜索算法找到的节点信息，将这些节点连接起来，形成完整的路径。这个过程通常需要从目标节点开始，沿着每个节点的父节点指针向上回溯，直到回溯到起始节点，从而找到一条完整的路径
            % 在 A* 算法中，重构路径通常是在找到目标节点后执行的，以便确定最佳路径，并将其用于后续的任务，比如路径规划、导航或者图形化显示
            if isequal(current.pos, targets(i, :))
                target_path = reconstructPath(current);
                break;
            end
            
            % openList(idx) = [];：这行代码用于从开放列表中移除已经处理过的节点。在A*算法中，开放列表通常用于存储待处理的节点，当算法对某个节点进行处理后，需要将其从开放列表中移除，以确保下次搜索时不会再次处理已经处理过的节点。通过将 idx 索引处的节点移除，可以实现这一操作。
            % closedList = [closedList current];：这行代码则是将当前处理的节点添加到关闭列表中。关闭列表通常用于存储已经处理过的节点，以避免对它们进行重复处理。在A*算法中，当一个节点被处理后，通常会将其添加到关闭列表中，以确保不会再次处理该节点。这样可以避免进入无限循环，也可以优化算法的性能
            % 从openList中移除具有最小f值的节点
            openList(idx) = [];
            % 确保下次搜索时不会再次处理已经处理过的节点
            closedList = [closedList current];
            
            % 通过for循环遍历四个方向（上、下、左、右）
            for dir = 1:size(directions, 1)
                
                % 当前节点位置加上对应方向的偏移
                neighbor = current.pos + directions(dir, :);
                % if neighbor(1) < 1 || neighbor(1) > size(grid, 1) || neighbor(2) < 1 || neighbor(2) > size(grid, 2)
                % neighbor(1) 是邻居节点的行索引，neighbor(2) 是邻居节点的列索引。
                % size(grid, 1) 返回地图 grid 的行数，size(grid, 2) 返回地图 grid 的列数。
                % 这个条件语句检查邻居节点是否超出了地图的边界范围：
                % neighbor(1) < 1 检查邻居节点的行索引是否小于1，即是否在地图的上方边界之外。
                % neighbor(1) > size(grid, 1) 检查邻居节点的行索引是否大于地图的行数，即是否在地图的下方边界之外。
                % neighbor(2) < 1 检查邻居节点的列索引是否小于1，即是否在地图的左侧边界之外。  
                % neighbor(2) > size(grid, 2) 检查邻居节点的列索引是否大于地图的列数，即是否在地图的右侧边界之外。
                % 如果邻居节点的行或列索引超出了地图边界范围的任何一侧，条件成立，说明邻居节点不在地图范围内，因此继续下一次循环处理下一个方向的邻居节点。
                % if grid(neighbor(1), neighbor(2)) == 1
                % 这行代码检查邻居节点是否为障碍物。
                % grid(neighbor(1), neighbor(2)) 获取地图中邻居节点的值，如果邻居节点在地图中的值为1，则表示它是一个障碍物。
                % 如果邻居节点是障碍物，条件成立，说明无法通过这个邻居节点进行移动，因此继续下一次循环处理下一个方向的邻居节点。
                % 检查邻居节点是否在地图范围内，如果邻居节点超出地图边界，则继续下一次循环
                if neighbor(1) < 1 || neighbor(1) > size(grid, 1) || neighbor(2) < 1 || neighbor(2) > size(grid, 2)
                    continue;
                end
                % 检查邻居节点是否为障碍物（grid中的值为1），如果是障碍物，则继续下一次循环
                if grid(neighbor(1), neighbor(2)) == 1
                    continue;
                end
                
                % 计算邻居节点的g值，即当前节点的g值加1，表示从当前节点到邻居节点的距离 
                % 计算邻居节点的h值，即启发式函数计算当前节点到目标点的估计距离。
                % 计算邻居节点的f值，即g值和h值的和
                % g = current.g + 1;
                % current.g 是当前节点到起始节点的实际代价（也称为路径长度）。
                % 1 表示从当前节点到其邻居节点的距离。在这里假设邻居节点之间的距离都是1，这是因为在许多路径规划问题中，邻居节点通常在相邻的单元格中，每次移动的成本是固定的。
                % g 表示从起始节点到当前邻居节点的实际代价，即路径长度。
                % h = heuristic(neighbor, targets(i, :));
                % heuristic 是一个启发式函数，用于估计从当前邻居节点到目标节点的代价。
                % neighbor 是当前邻居节点的位置。
                % targets(i, :) 是第 i 个目标节点的位置。
                % h 表示从当前邻居节点到目标节点的启发式估计代价。
                % f = g + h;
                % f 表示从起始节点经过当前邻居节点到目标节点的综合代价，是实际代价和启发式估计代价的和。
                % 综合代价 f 的计算是A*算法中的关键部分，它同时考虑了当前路径的实际代价和对目标的估计代价，帮助算法选择最有希望的节点进行扩展。
                g = current.g + 1;
                h = heuristic(neighbor, targets(i, :));
                f = g + h;
                % arrayfun(@(x) isequal(x.pos, neighbor), closedList) 的作用是检查 closedList 数组中的每个元素 x 是否与 neighbor 相等。如果 x.pos 与 neighbor 相等，则返回逻辑值 true，否则返回 false。这样就可以确定当前的邻居节点是否已经在 closedList 中了
                if any(arrayfun(@(x) isequal(x.pos, neighbor), closedList))
                    continue;
                end
                
                idx = find(arrayfun(@(x) isequal(x.pos, neighbor), openList));
                
                if ~isempty(idx)
                    if g < openList(idx).g
                        openList(idx).g = g;
                        openList(idx).f = f;
                        openList(idx).parent = current;
                    end
                else
                    openList = [openList struct('pos', neighbor, 'g', g, 'h', h, 'f', f, 'parent', current)];
                end
            end
        end
        
        iteration = iteration + 1;
    end
    
    path{i} = target_path;% 将找到的目标点i的路径target_path存储在cell数组path的第i个位置，即将当前目标点的路径存储起来
end


% % 标记起点和终点
% plot(start(2), start(1), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
% plot(end_point(2), end_point(1), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');

% % 显示障碍物
% [row, col] = find(grid == 1);
% plot(col, row, 'bs', 'MarkerSize', 10);

% 载入路障图片
obstacle_img = imread('3b47fb003d5d2eb42af403c7d62a254f.png');
% 可视化地图和路径
figure;
image(grid*255); % 将地图转换为灰度图像
colormap(ones(256,3)); % 使用全白色作为背景色
hold on;

% 显示障碍物图片
[row, col] = find(grid == 1);
for i = 1:length(row)
    x = col(i);
    y = row(i);
    image([x-0.5 x+0.5], [y-0.5 y+0.5], obstacle_img);
end
% 标记起点和终点
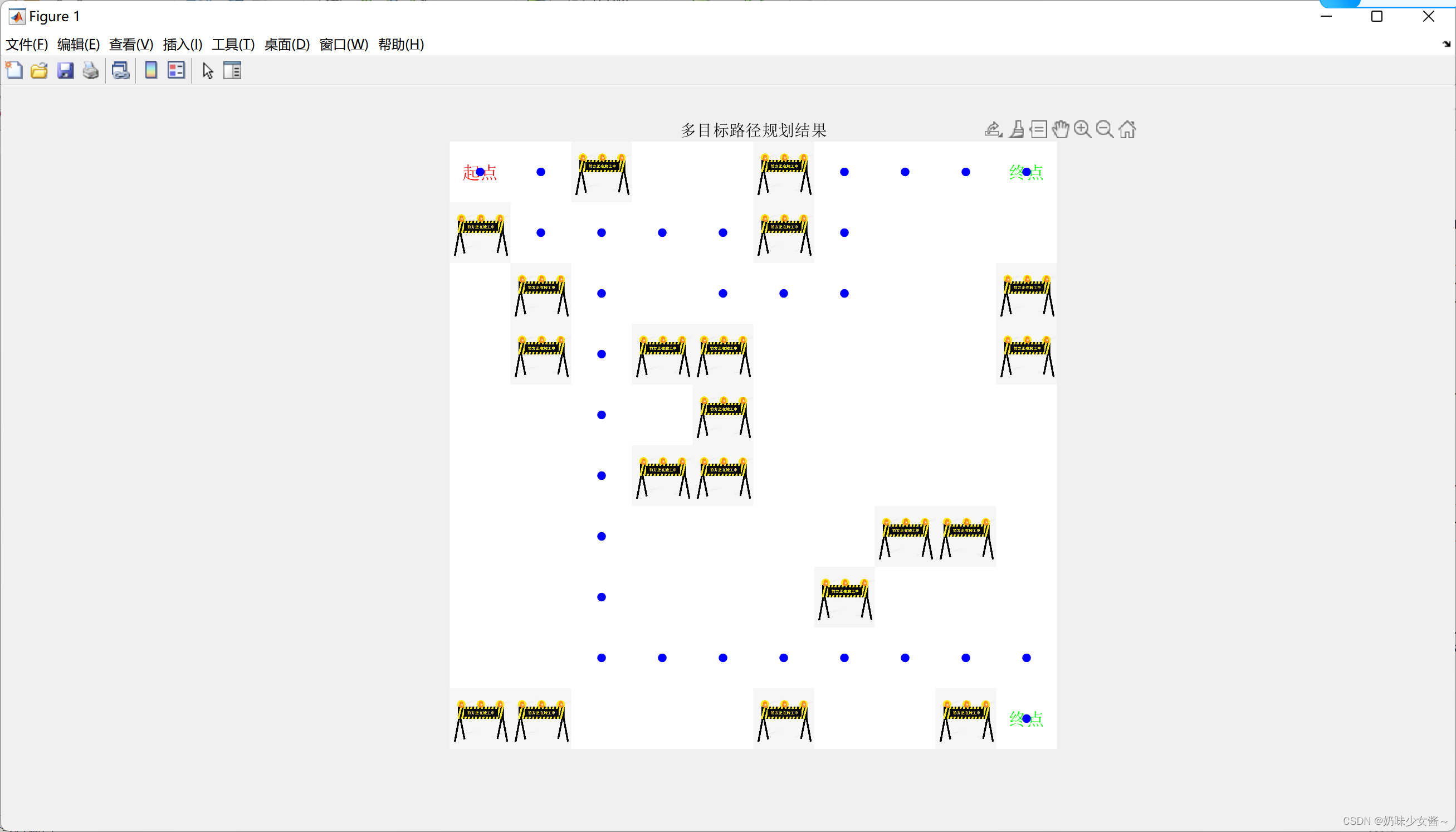
text(start(2), start(1), '起点', 'Color', 'red', 'FontSize', 12, 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle');
text(end_point(2), end_point(1), '终点', 'Color', 'green', 'FontSize', 12, 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle');
text(end_point_point(2), end_point_point(1), '终点', 'Color', 'green', 'FontSize', 12, 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle');

title('多目标路径规划结果');
% 显示路径
for i = 1:size(path, 2)
    for j = 1:size(path{i}, 1)
        plot(path{i}(j, 2), path{i}(j, 1), 'b.', 'MarkerSize', 20);
        pause(0.25); % 自动寻路的延时
    end
end


axis equal;
axis off;
hold off;

% A*算法实现  用于生成最终的路径结果
% 定义reconstructPath函数
function path = reconstructPath(node)
    path = [];
    while ~isempty(node)
        path = [node.pos; path];
        node = node.parent;
    end
end





% pos：表示节点的位置。这里使用变量start作为起始节点的位置。它是一个表示坐标的向量。
% g：表示从起始节点到当前节点的实际代价，即已经经过的路径长度。在这里，初始节点的实际代价被设置为0，因为还没有经过任何路径。
% h：表示启发式函数对当前节点到目标节点的估计代价。启发式函数在代码中通过调用heuristic函数来计算，通过传入start作为当前节点的位置，以及targets(i, :)作为目标节点的位置来计算估计代价。
% f：表示综合考虑实际代价和估计代价的综合代价值。在初始情况下，将初始节点的综合代价设置为0。后续会根据具体算法来更新这个值，通常是在拓展节点时根据实际代价和估计代价计算得出。
% parent：表示当前节点的父节点。初始情况下，父节点为空，因为这是起始节点。后续在路径搜索算法中，可以根据搜索过程来更新这个字段，用于还原最终路径