230.二叉搜索树的最小绝对差
- 二叉搜索树,用中序遍历
用一个全局变量result存储最小绝对差,prev指针存储
在中的逻辑里去更新result(保证prev不为空),然后更新prev=cur。
牢记谦虚遍历的顺序!pre紧跟在cur后面移动
class Solution {
int result = Integer.MAX_VALUE; //记录绝对差
TreeNode prev = null;
public void inorder(TreeNode cur) {
if(cur == null) return;
inorder(cur.left);
//中
if(prev!=null) {
result = Math.min(result, Math.abs(prev.val-cur.val));
}
prev = cur; //进到下一层递归之前,prev就等于cur
inorder(cur.right);
}
public int getMinimumDifference(TreeNode root) {
inorder(root);
return result;
}
}
501.二叉搜索树中的众数
- 二叉搜索树,一定是中序遍历
- 二叉搜索的性质,众数一定是连续出现的!—用双指针
怎么在一次遍历里找到maxCount和对应的数?
如果最后count=maxCount,就把这个元素放到result数组里。
定义全局变量
pre = null; int count = 0; //count统计单个元素出现的频率
int maxCount = 0; //统计遍历过的二叉树里元素出现的最高频率
List<Integer> result;
- 确定递归函数
void traversal(TreeNode cur)
- 终止条件
if(cur == null) return;
- 单层递归逻辑 中序 左中右
单层处理的逻辑:
- 一进来先更新count,分为三种情况
- 然后更新pre指针(此时pre就等于cur了)
- 接着看目前的count是否大于maxCount了。相等就加入result,更大了就清空result然后加入
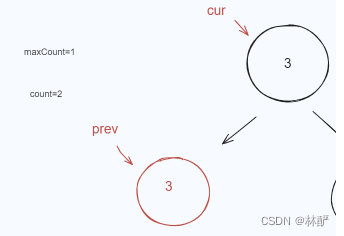
- 为什么加的是cur.val而不是pre.val?下面这个时候,在count++完,pre还没更新的时候,cur是指向3的!此时count=2 所以到后面加入result数组的是cur.val!
traversal(cur.left); //左
//中 就是处理的逻辑
if(pre == null) { //固定操作,说明刚开始遍历 cur指向第一个元素
count = 1;
}else if(pre.val == cur.val) { //pre不为空了,这个元素重复出现了
count++;
}else { //说明当前数值不相等了 cur第一次出现 count重置为1
count = 1;
}
pre = cur; //更新pre,跟着cur移动
if(count == maxCount) result.add(cur.val); //如果这个数出现频率和maxCount相等,放进去
else if(count > maxCount) {
maxCount = count; //更新maxCount
result.clear(); //清空result数组,之前旧的元素都不对了!
result.add(cur.val);
}
traversal(cur.right); //右
所谓的双指针就是,pre先初始化为null,两个指针同步遍历(pre更新就直接pre=cur)
通过判断count是否大于maxCount来添加元素,如果大于了就清空重新放。
- 完整代码
class Solution {
List<Integer> result = new ArrayList<>();
TreeNode pre = null;
int maxCount = 0;
int count = 0;
public void traversal(TreeNode cur) {
if(cur == null) return;
traversal(cur.left);
if(pre == null) {
count = 1;
}else if(pre.val == cur.val) {
count++;
}else {
count = 1;
}
pre = cur;
if(count == maxCount) {
result.add(cur.val);
}else if(count > maxCount) {
maxCount = count;
result.clear();
result.add(cur.val);
}
traversal(cur.right);
}
public int[] findMode(TreeNode root) {
traversal(root);
int[] res = new int[result.size()];
for (int i = 0; i < result.size(); i++) {
res[i] = result.get(i);
}
return res;
}
}
236.二叉树的最近公共祖先
注意:一个节点也可以是它自己的祖先
- 怎么从下往上遍历?
回溯啊!后序遍历的回溯过程。
判断某一个节点,左子树有没有出现过p,右子树有没有出现过q
只要左右子树出现了p和q就往上返回,如果左不为空右不为空的话就是最近的公共祖先
第二种情况:自己是自己的祖先
- 递归函数
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
- 确定终止条件
遇到空了 or 遇到了p或q,返回
if(root == null) return root;
if(root == p || root == q) return root;
- 单层递归逻辑 后序左右中
left = traversal(root.left,p,q); //相当于告诉我们左子树有没有出现过p q
right = traversal(root.right,p,q);
//左右都不为null 说明是公共祖先,往上返回
if(left!=null && right!=null) return root;
//左空右不为空,继续把右子树的往上返回
else if(left == null && right!=null) return right;
else if(left != null && right == null) return left;
else return null;
- 其实已经包含了第二种情况!遇到了自身是公共祖先的,就直接return root了,不去遍历下面的了!
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return root;
if(root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left,p,q); //相当于告诉我们左子树有没有出现过p q
TreeNode right = lowestCommonAncestor(root.right,p,q);
//左右都不为null 说明是公共祖先,往上返回
if(left!=null && right!=null) return root;
//左空右不为空,继续把右子树的往上返回
else if(left == null && right!=null) return right;
else if(left != null && right == null) return left;
else return null;
}
}