1、引言

小屌丝：鱼哥， 给我讲一讲LDA
小鱼：LDA？ 你指的是？

小屌丝：就是算法模型的LDA啊， 你想啥？
小鱼：哦，哦， 那就好，
小屌丝：你告诉我，你想啥了？
小鱼：不滴， 我就不
小屌丝：…你就说吧，我又不是外人
小鱼：…把耳朵凑过来，这只能悄悄说

小屌丝：鱼哥，你这… 咱不开车行不
小鱼：… 最近健身，骑自行车呢
小屌丝： … 我差点信了

小鱼：… 不扯了，咱还是开始 LDA吧。
小屌丝：那可不。

2、潜在狄利克雷分配

2.1 定义

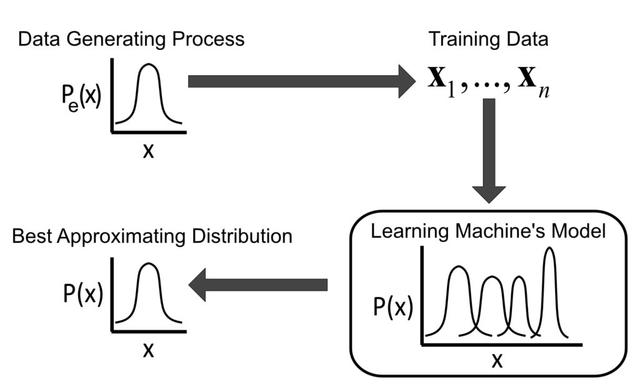
潜在狄利克雷分配（LDA）是一种生成概率模型，用于集合（如文档集合或语料库）的离散数据（如文档中的单词）的集合中发现潜在的结构。

在LDA中，每个文档被视为由多个主题的混合生成，而每个主题又是由词汇表中单词的特定概率分布所定义。

2.2 原理

LDA的核心原理在于假设文档是由潜在的主题混合而成的，而每个主题则由一组单词的概率分布来定义。

LDA通过最大化文档的似然性来估计这些主题和它们的单词分布。

在文档生成过程中，首先根据主题分布选择一个主题，然后根据该主题的单词分布生成一个单词。

这个过程在文档中重复进行，直到生成完整的文档。

2.3 算法公式

LDA的数学表达涉及概率图模型中的节点和边，以及相应的条件概率分布。

具体来说，LDA定义了一个文档集合中每篇文档的主题分布$（\theta ）$，每个主题的单词分布$（\phi ）$，以及文档的生成过程。

LDA的主要公式包括：

• 主题分布θ的先验分布：$Dirichlet(\alpha )$
• 单词分布φ的先验分布：$Dirichlet(\beta )$
• 文档中第n个词的主题分布：$z_{n}Multinomial(\theta )$
• 给定主题z_n，文档中第n个词的单词分布：KaTeX parse error: Double subscript at position 22: …Multinomial(φ_z_̲n)

其中，$\alpha$和$\beta$是超参数，分别控制主题分布和单词分布的稀疏性。

2.4 代码示例

# -*- coding:utf-8 -*-
# @Time   : 2024-01-21
# @Author : Carl_DJ

'''
实现功能：
    使用Python的gensim库实现LDA主题模型的
'''

import gensim  
from gensim import corpora  
from pprint import pprint  
  
# 假设我们有一些文档数据  
documents = [  
    "这是第一个文档。",  
    "这是第二个文档，与第一个文档相似。",  
    "第三个文档与前两个文档不同，讨论的是另一个主题。",  
]  
  
# 创建文本语料库  
texts = [[text for text in doc.split()] for doc in documents]  
dictionary = corpora.Dictionary(texts)  
corpus = [dictionary.doc2bow(text) for text in texts]  
  
# 使用LDA模型  
lda_model = gensim.models.LdaModel(corpus=corpus, id2word=dictionary, num_topics=2, random_state=100, update_every=1, chunksize=100, passes=10, alpha='auto', per_word_topics=True)  
  
# 打印主题  
pprint(lda_model.print_topics())  
  
 
# 获取文档的主题分布  
doc_topics = lda_model[corpus]  
for i, doc_topic in enumerate(doc_topics):  
    print(f"文档 {i} 的主题分布: {doc_topic}")  
  

• 打印主题 运行结果

#输出结果示例  
[(0, '0.237*"文档" + 0.196*"第一个" + 0.179*"这是" + 0.145*"相似" + 0.100*"第二个"'),  
(1, '0.263*"另一个" + 0.251*"主题" + 0.226*"讨论" + 0.140*"是" + 0.120*"不同"')]  

• 获取文档的主题分布运行结果

# 输出结果示例  
 文档 0 的主题分布: [(0, 0.9999911059222225)]  
 文档 1 的主题分布: [(0, 0.9999999999999997)]  
 文档 2 的主题分布: [(1, 0.9999999999999998)]

3、总结

潜在狄利克雷分配（LDA）是一种强大的无监督学习算法，它能够通过发现文档集合中的隐藏主题和主题分布，有效地揭示文档集合的内在结构。LDA的灵活性使其成为主题建模、文档分类、信息检索等多个任务中的理想选择。

LDA的核心在于它的生成式模型框架，该框架允许我们同时建模文档的主题混合和每个主题下的单词分布。通过最大化文档的似然性，LDA能够学习到这些分布，进而揭示出文档中的主题信息。

在实际应用中，LDA通常需要配合适当的预处理步骤（如分词、停用词去除、词干提取等）以及后续处理步骤（如主题可视化、主题解释等）来达到最佳效果。

此外，LDA的性能也受到一些因素的影响，如主题数量的选择、超参数的设定以及语料库的大小和质量等。

我是小鱼：

• CSDN 博客专家；
• 阿里云 专家博主；
• 51CTO博客专家；
• 企业认证金牌面试官；
• 多个名企认证&特邀讲师等；
• 名企签约职场面试培训、职场规划师；
• 多个国内主流技术社区的认证专家博主；
• 多款主流产品(阿里云等)测评一、二等奖获得者；

关注小鱼，学习【机器学习】&【深度学习】知识，不再迷路。