前言:剑指offer刷题系列
问题:
给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
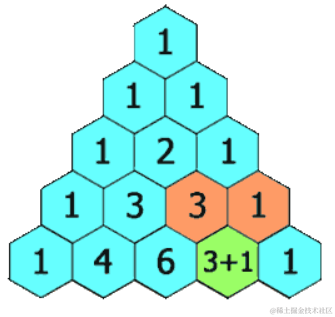
示例:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
思路:
杨辉三角是小学就学过的一种方法,看着还挺熟悉,所以没有花费很多时间理解(学名叫做 帕斯卡三角形 的数学模型),帕斯卡三角形是一个由数字构成的三角形,其中每个数字是肩膀上方两个数字之和,一直做金字塔下延。
这个函数接受一个名为 numRows 的整数作为输入,并返回一个二维列表,表示「杨辉三角」的前 numRows 行。下面是详细的思考过程。
- 首先,定义一个名为
Solution的 Python 类。这个类将包含一个方法generate,它接受一个整数参数numRows,用于指定要生成的行数。方法的返回值将是一个二维列表,其中包含了帕斯卡三角形模型的前numRows行。 - 在
generate方法中,创建一个空列表triangle,用于存储生成的三角形。 - 使用外层循环
for i in range(numRows)来控制生成的行数。在每次循环中,创建一个空列表row,用于存储当前行的元素。 - 在内层循环
for j in range(1, i)中,通过访问上一行的元素来计算当前行的元素值。具体地说,将当前元素设置为上一行中相邻两个元素之和:row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]。 - 完成内层循环后,将当前行
row添加到triangle列表中。 - 外层循环结束后,返回存储了帕斯卡三角形模型的二维列表
triangle。
基于上述思考,代码如下:
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
triangle = []
for i in range(numRows):
row = [1] * (i + 1)
for j in range(1, i):
row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]
triangle.append(row)
return triangle
执行结果如下图:
学到的知识点:
学会如何使用帕斯卡三角形模型生成特定行数的三角形。
今天突然发现之前参加的一个活动快要结束了,但是我的任务还没有做完,要抓紧做一下任务,不然自己的心血啊都要泡汤了。