机器学习：数据降维主成分分析PCA

一、引言

1.数据分析的重要性
在当今的信息爆炸时代，数据已经渗透到各个行业和领域的每一个角落，成为决策制定、科学研究以及业务发展的重要依据。数据分析则是从这些数据中提取有用信息、发现潜在规律的关键手段。通过数据分析，我们能够更深入地了解问题的本质，把握市场趋势，优化业务流程，提高决策效率，从而为企业和社会创造更大的价值。
2.引出降维的需求与意义
然而，在实际的数据分析过程中，我们往往面临着数据维度过高的问题。高维数据不仅增加了计算复杂度和存储成本，而且可能导致“维度灾难”，使得数据分析变得困难重重。此外，高维数据中的许多变量之间可能存在相关性，导致信息冗余和干扰。因此，降维成为了数据分析中不可或缺的一环。通过降维，我们可以去除冗余变量，降低数据复杂度，提高分析效率，同时保留数据中的主要信息。
3.主成分分析（PCA）的概念及其在数据分析中的角色
主成分分析（PCA）是一种广泛应用的降维方法，它通过线性变换将原始的高维数据映射到一个低维空间中，同时尽可能保留数据中的主要变化模式。PCA的基本思想是将数据中的多个变量通过线性组合的方式转化为少数几个互不相关的综合变量，这些综合变量称为主成分。每个主成分都是原始变量的线性组合，它们按照方差大小进行排序，第一个主成分具有最大的方差，即保留了数据中的最大变化信息。通过选择前几个主成分，我们可以在降低数据维度的同时保留大部分的信息。

在数据分析中，PCA扮演着重要的角色。它不仅可以用于数据的可视化、去噪和压缩，还可以作为其他机器学习算法的预处理步骤，提高算法的性能和稳定性。此外，PCA还可以用于特征提取和降维后的数据解释，帮助我们更深入地理解数据的结构和内在规律。

一句话概括主成分分析

主成分分析是采取一种数学降维的方法，找出几个综合变量来代替原来众多的变量，使这些综合变量能尽可能地代表原来变量的信息量，而且彼此之间互不相关。这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。

二、主成分分析的基本概念

1、PCA的定义与原理

主成分分析（Principal Component Analysis，简称PCA）是一种统计分析方法，它旨在通过正交变换将原始特征空间中的线性相关变量转换为新的线性无关变量，即主成分。这些主成分能够保留原始数据的大部分信息，同时降低数据的维度，使得数据的处理和分析更加高效。

PCA的原理基于数据的方差最大化思想。方差代表了数据的离散程度，方差越大，说明数据在该维度上的变化越丰富，所包含的信息也就越多。因此，PCA通过找到一个正交变换矩阵，将原始数据投影到一个新的坐标系中，使得投影后的数据在每个维度上的方差尽可能大。这些新的维度就是主成分，它们之间互不相关，且能够尽可能多地保留原始数据的信息。

具体来说，PCA的实现过程包括以下几个步骤：

数据标准化：将原始数据进行标准化处理，消除量纲和数值大小对分析结果的影响。
计算协方差矩阵：计算标准化后数据的协方差矩阵，反映各变量之间的相关性。
特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量。
选择主成分：根据特征值的大小选择前k个主成分，通常选择累计贡献率达到一定阈值（如80%）的前k个主成分。
转换数据：将原始数据转换到由前k个主成分构成的新坐标系中，得到降维后的数据。

2、PCA与其他降维方法的比较

PCA与线性判别分析（LDA）、t-SNE等降维方法有着各自的特点和适用场景。

LDA是一种监督学习的降维技术，它在降维的同时考虑了类别信息，使得投影后的数据类内方差最小，类间方差最大。因此，LDA在分类问题中表现较好。然而，LDA需要数据的类别标签，这使得它在无监督学习场景中受到限制。

相比之下，PCA是一种无监督的降维方法，它不需要数据的类别标签，仅基于数据的方差进行降维。这使得PCA在探索性数据分析和预处理阶段具有广泛的应用。PCA通过最大化投影方差来保留数据的主要信息，但可能忽略了与类别相关的信息。

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种用于高维数据可视化的降维方法。它通过保留数据点之间的局部相似性来将高维数据映射到二维或三维空间中，以便进行可视化。t-SNE在可视化复杂结构和发现数据中的簇群方面表现出色，但计算成本较高，且对参数的选择较为敏感。

综上所述，PCA、LDA和t-SNE等降维方法各有其特点和适用场景。在选择降维方法时，需要根据具体任务和数据特点进行权衡和选择。例如，在无监督学习场景中，PCA可能是一个更好的选择；而在分类问题中，LDA可能更具优势；对于需要可视化高维数据的情况，t-SNE则是一个有力的工具。

三、PCA的数学描述

PCA的原理图如下所示：
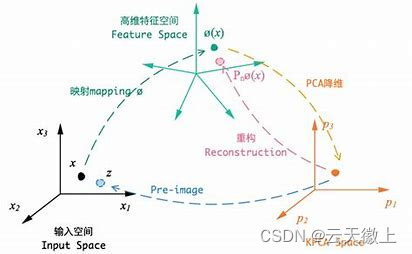
在这里插入图片描述

主成分分析的数学形式描述的计算步骤如下：
1）设原始变量 $X_1,X_2,\cdots,X_p$ 的 $n$ 次观测数据矩阵为：
$X=\left[ \begin{matrix} x_{11} & x_{12} & \cdots & x_{1p}\\ x_{21} & x_{22} & \cdots & x_{2p}\\ \vdots & \vdots & \vdots & \vdots\\ x_{n1} & x_{n2} & \cdots & x_{np}\\ \end{matrix} \right]=(X_1,X_2,\cdots,X_p)$
2) 将数据矩阵按列进行中心标准化。为了方便，将标准化后的数据矩阵仍然记为 $X$ 。
3）求相关系数矩阵 $R$ , $R=(r_{ij})_{p*p}$ , $r_{ij}$ 的定义为：
$r_{ij}=\sum_{k=1}^{n}(x_{ki}-\bar{x_i})(x_{kj}-\bar{x_j})/\sqrt{\sum_{k = 1}^{n} (x_{ki}-\bar{x_i})^2+ \sum_{k = 1}^{n} (x_{kj}-\bar{x_j})^2}$
其中， $r_{ij}=r_{ji}$ , $r_{ii}=1$ 。
4）求 $R$ 的特征方程 $det(R-\lambda E)=0$ 的特征根 $\lambda_1 \geq \lambda_2 \geq \lambda_p > 0$ 。
5）确定主成分的个数 $m$ : $\frac{\sum_{i=1}^{m}\lambda_i}{\sum_{i=1}^{P}\lambda_i} \geq \alpha$ , $\alpha$ 根据实际问题确定，一般取80%。
6）计算 $m$ 个相应的单位特征向量：
$\beta_1 = \left [\begin{array}{cccc} \beta_{11} \\ \beta_{21} \\ . \\ . \\ . \\ \beta_{p1} \\ \end{array}\right], \beta_1 = \left [\begin{array}{cccc} \beta_{12} \\ \beta_{22} \\ . \\ . \\ . \\ \beta_{p2} \\ \end{array}\right],...,\beta_1 = \left [\begin{array}{cccc} \beta_{1m} \\ \beta_{2m} \\ . \\ . \\ . \\ \beta_{pm} \\ \end{array}\right]$
7) 计算主成分：
$Z_i = \beta_{1i}X_1+\beta_{2i}X_2+...+\beta_{pi}X_p, i=1,2,...,m$

至此整个PCA算法的流程整个推理结束。在python中，主成分分析的函数位于Scikit-Learn下：

sklearn.decomppsition.PCA(n_componets=None, copy=True, whiten=False)

参数说明：

( 1 ) n_components
意义:PCA 算法中所要保留的主成分个数n，也即保留下来的特征个数n。
类型:int或者string，缺省时默认为None，所有成分被保留。赋值为int，比如n_compo-nents=1，将把原始数据降到一个维度。赋值为string，比如n_components=‘mle’，将自动选取特征个数n，使得满足所要求的方差百分比。
( 2 ) copy
类型: bool，True或者False，缺省时默认为True。
意义:表示是否在运行算法时，将原始训练数据复制一份。若为True，则运行PCA算法后，原始训练数据的值不会有任何改变，因为是在原始数据的副本上进行运算;若为False，则运行PCA算法后，原始训练数据的值会改，因为是在原始数据上进行降维计算。
( 3 ) whiten
类型:bool，缺省时默认为False。
意义:白化，使得每个特征具有相同的方差。

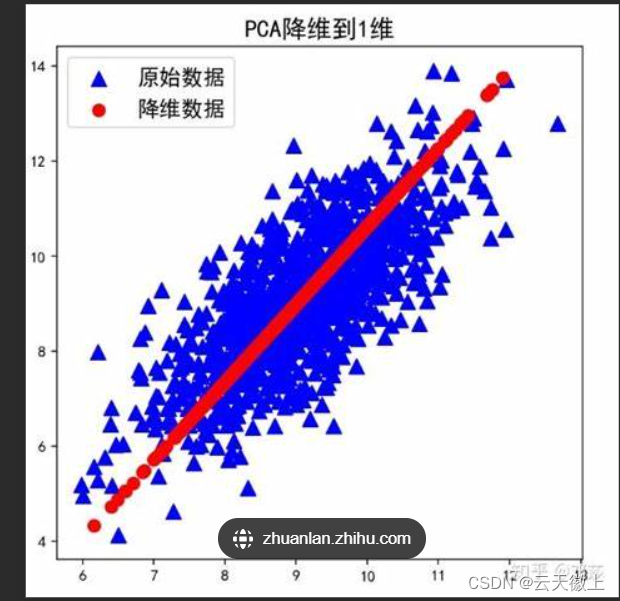
将数据降维到一维的情况下的图片如下所示：
在这里插入图片描述

四、PCA的优缺点分析

1、PCA的优点

降低数据维度，简化模型：PCA通过正交变换将原始的高维数据映射到低维空间，显著减少了数据的维度，从而简化了后续的数据处理和模型训练过程。这不仅可以提高计算效率，还可以减少过拟合的风险，使得模型更加稳健。

保留数据中的主要变化模式：PCA通过最大化投影方差的方式，保留了数据中的主要变化模式。这意味着降维后的数据仍然能够反映原始数据的主要特征和结构，从而保证了信息的有效传递。

去除噪声和冗余信息：PCA能够去除数据中的噪声和冗余信息，提高数据的信噪比。这对于提高数据分析的准确性和可靠性具有重要意义。通过去除不重要的变量和相关性较强的变量，PCA可以帮助我们更好地聚焦于关键信息。

2、PCA的缺点

对数据的线性关系敏感：PCA是一种基于线性变换的降维方法，它假设数据之间的关系是线性的。然而，在实际情况中，数据之间可能存在复杂的非线性关系。在这种情况下，PCA可能无法有效地捕捉数据的内在结构，导致信息丢失或失真。

可能丢失非线性结构信息：由于PCA是基于线性变换的，它可能无法有效地处理具有非线性结构的数据。当数据中存在复杂的非线性关系时，PCA可能无法准确地揭示这些关系，从而导致信息的损失。

对缺失值和异常值敏感：PCA对数据的完整性要求较高，对缺失值和异常值较为敏感。缺失值可能导致协方差矩阵的计算不准确，从而影响PCA的结果；而异常值则可能导致主成分的选择出现偏差。因此，在使用PCA之前，通常需要对数据进行预处理，以消除缺失值和异常值的影响。

五、PCA的实际应用领域

1、图像识别与处理

在图像识别与处理领域，PCA发挥着重要作用。由于图像数据往往维度巨大，包含大量的像素点，直接处理这类数据不仅计算量大，而且容易遭遇“维度灾难”。通过PCA，我们可以将高维的图像数据转换为低维表示，同时保留图像的主要特征。这种方法在图像压缩、去噪、特征提取等方面都有广泛应用。例如，在人脸识别系统中，PCA可以用于提取人脸的主要特征，降低识别算法的复杂度，提高识别准确率。

2、基因组学数据分析

在基因组学研究中，PCA同样展现出了其强大的应用潜力。基因表达数据通常包含成千上万个基因的表达水平，数据维度极高。通过PCA，我们可以将这些高维数据转换为少数几个主成分，从而更好地理解基因之间的相互作用和调控关系。这有助于揭示基因与疾病、表型之间的关联，为疾病的预防和治疗提供新的思路。

3、金融市场分析

金融市场分析中，PCA也被广泛应用。金融数据通常包含大量的股票价格、汇率、宏观经济指标等变量，这些变量之间可能存在复杂的相关性。通过PCA，我们可以将这些变量转换为少数几个主成分，从而简化分析过程，揭示金融市场的内在结构。这有助于投资者更好地理解市场走势，制定更有效的投资策略。

4、其他领域的应用举例

除了上述领域外，PCA在其他领域也有广泛的应用。例如，在化学领域，PCA可以用于分析化学物质的组成和结构；在生物医学领域，PCA可以用于研究生物分子的相互作用和信号传导机制；在环境科学领域，PCA可以用于分析环境污染物的来源和分布等。

六、PCA的注意事项与技巧

1、选择合适的主成分数量

选择合适的主成分数量是PCA应用中的关键步骤。主成分数量过多可能导致模型过于复杂，而过少则可能丢失重要信息。一种常用的方法是观察主成分贡献率的累积百分比，选择累积贡献率达到一定阈值（如80%）的主成分数量。此外，还可以结合业务背景和实际需求，选择具有实际意义的主成分。

2、数据预处理的重要性

PCA对数据的质量和完整性要求较高，因此数据预处理至关重要。首先，需要对数据进行标准化处理，消除量纲和数值大小对分析结果的影响。其次，需要处理缺失值和异常值。对于缺失值，可以采用插值、删除或填充等方法进行处理；对于异常值，则需要进行检测并视情况进行处理或剔除。

3、PCA与其他机器学习方法的结合使用

PCA作为一种特征提取和降维工具，可以与其他机器学习方法结合使用，以提高模型的性能。例如，PCA可以作为分类、聚类或回归等算法的预处理步骤，通过降低数据维度和去除噪声，提高后续算法的准确性和效率。此外，PCA还可以与深度学习、神经网络等复杂模型结合，共同解决复杂的数据分析问题。

4、零均值化

当对训练集进行 PCA 降维时，也需要对验证集、测试集执行同样的降维。而对验证集、测试集执行零均值化操作时，均值必须从训练集计算而来，不能使用验证集或者测试集的中心向量。

其原因也很简单，因为我们的训练集时可观测到的数据，测试集不可观测所以不会知道其均值，而验证集再大部分情况下是在处理完数据后再从训练集中分离出来，一般不会单独处理。如果真的是单独处理了，不能独自求均值的原因是和测试集一样。

另外我们也需要保证一致性，我们拿训练集训练出来的模型用来预测测试集的前提假设就是两者是独立同分布的，如果不能保证一致性的话，会出现 Variance Shift 的问题。

七、PCA的实现案列

主成分分析降维代码

import pandas as pd

#参数初始化
inputfile = '../data/components.xls'    #降维前的数据地址
outputfile = '../tmp/dimention.xls'     #降维后的数据地址

data = pd.read_excel(inputfile, header = None） #读入数据

from sklearn.decompostion import PCA

pac = PCA()
pca.fit(data)
pca.components_   #返回模型的各个特征向量
pca.explained_variance_ratio_  #返回各个成分各自的方差百分比

pca.components_  #返回模型的各个特征向量

array( [ [-0.56788461，-0.2280431 , -0.23281436，-0.22427336，-0.3358618 ,
          -0.43679539,-0.03861081,-0.46466998],
         [-0.64801531,-0.24732373,0.17085432，0.2089819 , 0.36050922,
           0.55908747,-0.00186891,-0.05910423],
         [-0.45139763，0.23802089,-0.17685792，-0.11843804,-0.05173347,
          -0.20091919,-0.00124421, 0.80699041],
         [-0.19404741,0.9021939,-0.00730164,-0.01424541,0.03106289,
           0.12563004,0.11152105,-0.3448924 ],
         [ 0.06133747,0.03383817，-0.12652433,-0.64325682，0.3896425 ,
           0.10681901, -0.63233277,-0.04720838],
         [-0.02579655,0.06678747,-0.12816343,0.57023937,0.577124,   
         0.10681901, -0.63233277,-0.04720838],                 
         [ 0.03800378，-0.09520111,-0.15593386,-0.34300352，  
         0.10681901, -0.63233277,-0.04720838],
         [ 0.10147399，-0.03937889，-0.91023327,0.18760016,-0.06193777,
           0.34598258,0.02090066,-0.02137393]])

pca.explained_variance_ratio_#返回各个成分各自的方差百分比（贡献率)

array([7.74011263e-01, 1.56949443e-01, 4.27594216e-02,
          2.40659228e-02, 1.50278048e-03, 4.10990447e-04,
          2.07718405e-04, 9.24594471e-05])

从上面的结果可以得到特征方程 $det(R-\lambda E)=0$ 有7个特征根、对应的7个单位特征向量以及各个成分各自的方差百分比(也称为贡献率)。其中，方差百分比越大，说明向量的权重越大。
当选取前4个主成分时，累计贡献率已达到97.37%，说明选取前3个主成分进行计算已经相当不错了，因此可以重新建立PCA模型，设置n_components =3，计算出新的成分结果。

PCA算法在iris数据集上的应用案列

import numpy as np
from sklearn import decomposition,datasets
iris=datasets.load_iris()#加载数据
X=iris['data']
model=decomposition.PCA(n_components=2)
model.fit(X)
X_new=model.fit_transform(X)
Maxcomponent=model.components_
ratio=model.explained_variance_ratio_
score=model.score(X)
print('降维后的数据:',X_new)
print('返回具有最大方差的成分:',Maxcomponent)
print('保留主成分的方差贡献率:',ratio)
print('所有样本的log似然平均值:',score)
print('奇异值:',model.singular_values_)
print('噪声协方差:',model.noise_variance_)
g1=plt.figure(1,figsize=(8,6))
plt.scatter(X_new[:,0],X_new[:,1],c='r',cmap=plt.cm.Set1, edgecolor='k', s=40)
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('After the dimension reduction')
plt.show()

八、总结与展望

总结PCA的核心思想与实际应用价值

PCA作为一种强大的数据降维技术，在数据分析领域具有广泛的应用价值。其核心思想是通过线性变换将原始数据转换为低维表示，同时保留数据中的主要变化模式。通过PCA，我们可以降低数据维度、去除噪声和冗余信息，提高数据分析的效率和准确性。在实际应用中，PCA已被广泛应用于图像识别与处理、基因组学数据分析、金融市场分析等多个领域，为这些领域的发展提供了有力的支持。

展望PCA的未来发展趋势与研究方向

随着大数据和人工智能技术的快速发展，PCA作为一种基础的数据分析工具，其重要性日益凸显。未来，PCA将在更多领域得到应用，并与更多先进的技术和方法结合，共同推动数据分析领域的发展。同时，随着数据的复杂性和多样性的增加，PCA算法本身也需要不断优化和改进，以适应新的数据分析需求。例如，可以研究如何将非线性变换引入PCA中，以更好地处理非线性数据；还可以探索如何将PCA与深度学习等先进技术结合，以提高数据分析的准确性和效率。总之，PCA作为一种经典的数据分析方法，其未来发展前景广阔，值得我们继续关注和研究。