本文主要介绍图神经网络相关内容,包括图神经网络的基本结构以及近期研究进展。
背景
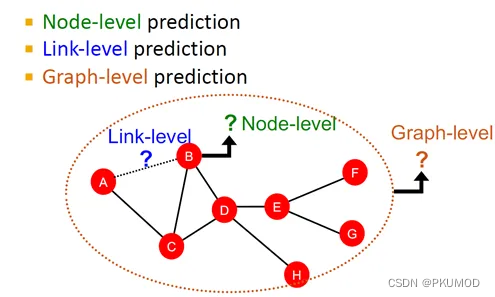
在实际生活中,许多数据都可以用图的形式表达,比如社交网络、分子模型、知识图谱、计算机网络等。图深度学习旨在,显式利用这些数据中的拓扑结构信息,达到更好的预测效果。具体来说,如下图所示,给定一个图,我们主要关注的机器学习任务包括:节点级别的预测,链接级别的预测,图级别的预测等。
节点级别预测任务
节点级别的预测指的是我们需要为图中的每个节点输出一个预测值。
链接级别预测任务
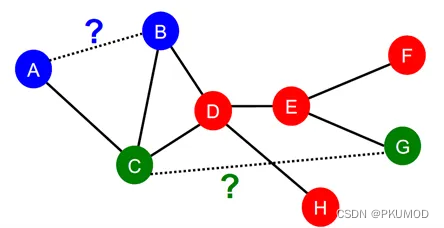
链接预测任务需要我们为节点对输出一个预测值。例如,判断下图中AB两点、CG两点间是否可能存在缺失的边。
图级别预测任务
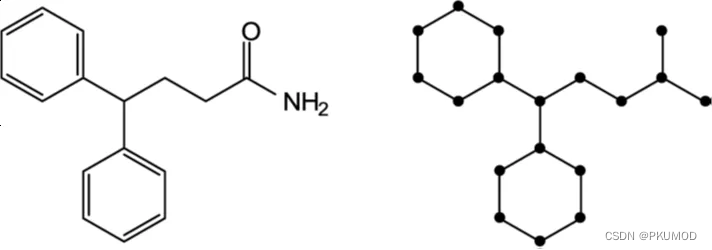
图级别预测任务需要我们对整个图输出一个预测值。例如,我们想要判定下图所示分子具有的某些性质,此时我们应该将整个分子图作为输入,在图级别上进行预测。
图表征学习
由上面的例子出发,我们总结图表征学习的一个主要内容,就是将图中的节点映射到d维的向量空间,使得相似的节点同样具有相近的向量表示,如下图所示。最重要的问题就是,如何学习得到映射函数 f f f?
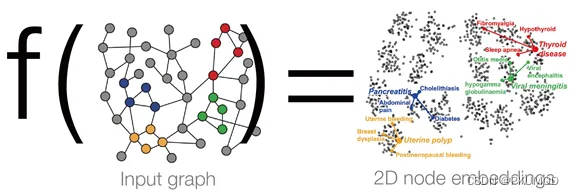
简单的表征方法
具体来说,我们需要学习一个编码器ENC:
E
N
C
(
v
)
=
z
v
,
ENC(v)=\mathbf{z}_v,
ENC(v)=zv,
其中
v
v
v是图中的节点,
z
v
∈
R
d
z_v\in \mathbb{R}^d
zv∈Rd则是它对应的向量表示。最简单的方法就是设立一个
N
×
d
N×d
N×d的表(矩阵)(
N
N
N是图中节点的数量),其中矩阵第
i
i
i行对应图中第
i
i
i个节点的向量表示,即
Z
=
[
z
0
T
,
z
1
T
,
…
,
z
N
−
1
T
]
T
.
\mathbf{Z}=[\mathbf{z}_0^T,\mathbf{z}_1^T,…,\mathbf{z}_{N-1}^T ]^T.
Z=[z0T,z1T,…,zN−1T]T.
通过训练得到合适的矩阵
Z
\mathbf{Z}
Z,我们便可以得到图的向量表示。然而,尽管这种方法实际上已经广泛应用于知识图谱嵌入(Knowledge graph embedding)方法中,它也具有一些内在的缺陷。
首先,显而易见,要表达整个图我们需要训练的参数共有O(Nd)个。这种方法不仅需要大量的参数,同时每个节点的表示都是独一无二、没有交集的(不同节点对应于矩阵的不同行)。其次,这种方法无法表示训练中未曾出现的节点。最后,这种方法也很难考虑图中可能含有的节点特征。综上所述,我们需要一种新的方法来避免上述的问题。
图深度学习
在图深度学习中,我们考虑使用多层的非线性变换来构成一个映射f,而这种编码器需要考虑到图所天然具有的两种性质:
-
置换不变性:
f ( A , X ) = f ( P A P T , P X ) , f(\mathbf{A,X})=f(\mathbf{PAP}^T,\mathbf{PX}), f(A,X)=f(PAPT,PX),
其中 A \mathbf{A} A是图的邻接矩阵, X \mathbf{X} X是图的节点特征而 P \mathbf{P} P是某个置换。在此种情况内,我们需要保证无论图的节点输入顺序如何变化, f f f的输出始终保持不变。这种情况对应于将整个图映射到一个向量,即图级别的预测任务。 -
置换等变性:
P f ( A , X ) = f ( P A P T , P X ) , \mathbf{P}f(\mathbf{A,X})=f(\mathbf{PAP}^T,\mathbf{PX}), Pf(A,X)=f(PAPT,PX),
在此种情况内,我们需要保证无论图的节点输入顺序如何变化,f的输出始终保持同样的变换。这种情况对应于将整个图映射到一个N×d维矩阵,即节点级别的预测任务。
消息传递神经网络
消息传递神经网络就是一类典型的具有置换等变性的模型。其中,一类具有代表性的方法就是图卷积网络(GCN)。它的计算过程可总结如下(针对无向图):
h
v
(
0
)
=
x
v
,
\mathbf{h}_v^{(0)}=\mathbf{x}_v,
hv(0)=xv,
h
v
(
l
+
1
)
=
σ
(
W
∣
N
(
v
)
∣
∑
u
∈
v
∪
{
u
}
h
u
(
l
)
)
,
\mathbf{h}_v^{(l+1)}=\sigma\left(\frac{\mathbf{W}}{|\mathcal{N}(v)|}\sum_{u\in\mathcal{v}\cup\{u\}}\mathbf{{h}_u^{(l)}}\right),
hv(l+1)=σ
∣N(v)∣Wu∈v∪{u}∑hu(l)
,
z
v
=
h
v
(
L
)
,
\mathbf{z}_v=\mathbf{h}_v^{(L)},
zv=hv(L),
其中,
x
v
\mathbf{x}_v
xv是节点
v
v
v对应的节点特征,
N
(
v
)
\mathcal{N}(v)
N(v)是节点
v
v
v的邻居节点集合,
W
l
\mathbf{W}_l
Wl是第
l
l
l层网络的参数。可以看出,它的计算过程主要包含两步:第一步是聚合邻居节点的信息,第二步则是将得到的信息通过非线性映射来得到下一层的表示。每一层都可看作是如下图所示的计算过程,而我们将具有这种计算过程的神经网络统称为消息传递神经网络。
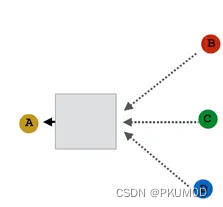
那么,消息传递神经网络什么时候表达能力最强呢?(这里,表达能力是指区分不同输入的能力。)一个结论是,当上图中方盒子对应的函数为单射函数时,模型的表达能力最强,而GIN[10]就是这样的神经网络。在每一层,它更新的方法为
h
v
(
l
+
1
)
=
M
L
P
Φ
(
(
1
+
ϵ
)
⋅
M
L
P
f
(
h
v
(
l
)
)
+
∑
u
∈
N
(
v
)
M
L
P
f
(
h
u
(
l
)
)
)
,
\mathbf{h}_v^{(l+1)}=\rm{MLP}_\Phi\left((1+ϵ)⋅\rm{MLP}_f (\mathbf{h}_v^{(l)} )+∑_{u∈N(v)} \rm{MLP}_f (\mathbf{h}_u^{(l)} )\right),
hv(l+1)=MLPΦ
(1+ϵ)⋅MLPf(hv(l))+u∈N(v)∑MLPf(hu(l))
,
其中,
M
L
P
\rm{MLP}
MLP是多层感知机,
ϵ
ϵ
ϵ是可学习的实数。
消息传递神经网络的限制
消息传递神经网络的表达能力受限于Weisfeiler-Lehman(WL)图同构算法,它的过程如下:给定一个图,首先对每个节点v赋予一个初始颜色c^0 (v) ,而后迭代地更新节点颜色:
c
l
+
1
(
v
)
=
H
A
S
H
(
c
l
(
v
)
,
{
c
l
(
u
)
│
u
∈
N
(
v
)
}
)
,
c^{l+1} (v)=HASH\left(c^l (v),\{c^l (u)│u∈\mathcal{N}(v) \}\right),
cl+1(v)=HASH(cl(v),{cl(u)│u∈N(v)}),
其中
H
A
S
H
HASH
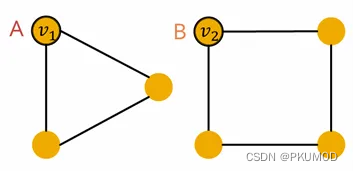
HASH是单射的哈希函数。如果两个图可以被GIN所区分,那么它们也可以被WL算法区分,反之亦然。这样,一些关于WL测试已有的结论,就可以方便地应用在消息传递神经网络上。例如下图所示的两个图,GIN无法区分图A中的节点
v
1
v_1
v1与图B中的节点
v
2
v_2
v2.
图神经网络的近期进展
为提高图神经网络的表达能力,近期人们提出了多种不同的图神经网络模型。在这里,我们主要介绍两类:Higher-order GNNs,包括k-GNNs[1],k-FGNNs[2],k-Local GNNs[3]等;Subgraph GNNs[4]。其它的方法也有很多,如Graph Transformers with distance encoding [5] ,GNNs with lifting transformations [6]等,在此不再赘述。
Higher-order GNNs
该部分内容主要取自 Christopher Morris et al, “Weisfeiler and Leman Go Neural: Higher-order Graph Neural Networks”, AAAI 2019.它的基本思想是,模仿WL 图同构算法的拓展版本k-WL算法:与原始WL算法的不同点在于,我们为图中的 k k k维节点组赋予一个颜色:: c ( v ) c(v) c(v) 其中 v ∈ V k v∈V^k v∈Vk。在第l次迭代,计算
c
l
+
1
(
v
)
=
H
A
S
H
(
c
l
(
v
)
,
c
l
+
1
(
v
,
1
)
,
…
,
c
l
+
1
(
v
,
k
)
)
for
v
∈
V
k
,
c^{l+1} (\mathbf{v})=HASH(c^l (\mathbf{v}),c^{l+1} (\mathbf{v},1),…,c^{l+1} (\mathbf{v},k)) \text{ for } \mathbf{v}∈V^k,
cl+1(v)=HASH(cl(v),cl+1(v,1),…,cl+1(v,k)) for v∈Vk,
c
l
+
1
(
v
,
i
)
=
c
l
(
w
)
∣
w
∈
N
i
(
v
)
for
i
∈
[
k
]
,
v
∈
V
k
,
c^{l+1} (\mathbf{v},i)={{c^l (\mathbf{w})|\mathbf{w}∈\mathcal{N}_i (\mathbf{v})}}\text{ for }i∈[k],\mathbf{v}∈V^k,
cl+1(v,i)=cl(w)∣w∈Ni(v) for i∈[k],v∈Vk,
其中 N i ( v 1 , … , v k ) = ( v 1 , … , v i − 1 , w , v i + 1 , … , v k ) ∣ w ∈ V N_i (v_1,…,v_k )={(v_1,…,v_{i-1},w,v_{i+1},…,v_k)|w∈V} Ni(v1,…,vk)=(v1,…,vi−1,w,vi+1,…,vk)∣w∈V. 对于任意的k≥3,k-WL的表达能力严格大于(k-1)-WL。k-GNNs从上面的k-WL算法出发,提出了一个类似的神经网络结构,来学习图的向量表征。
Subgraph GNNs
该部分内容主要取自Beatrice Bevilacqua et al., “Equivariant Subgraph Aggregation Networks”, ICLR 2022. 作者的动机来源于,尽管两个图也许不能被消息传递神经网络所区分,但它的子图或许可以被区分。举例来说,如下图所示。在原图中删去一条边,则可以得到一个子图。针对原图中的每一条边都删除一次,可以得到7个子图。而在这7个子图上进行WL算法,可以发现,原本无法区分的两个图,现在可以通过这些子图加以区分。
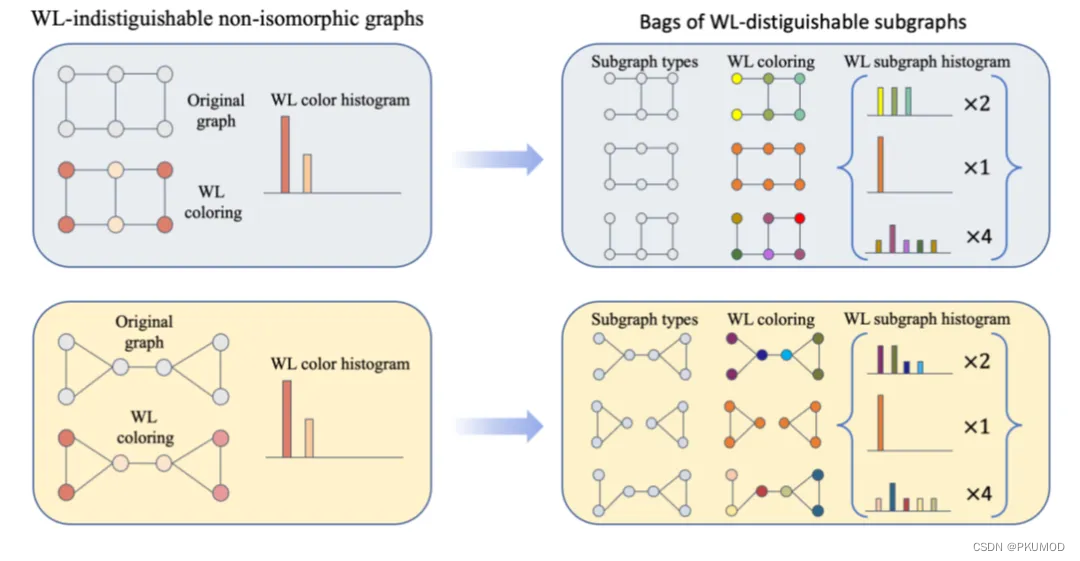
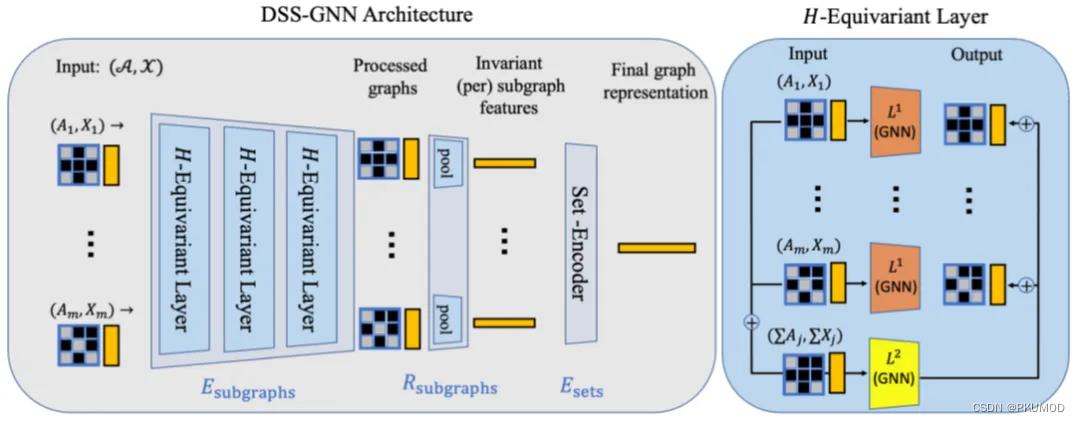
受此启发,作者提出了Equivariant Subgraph Aggregation Networks (ESAN),它的基本框架如下。主要思想是,将图 G G G 表达为一组子图 B G = G 1 , … , G m B_G={{G_1,…,G_m }} BG=G1,…,Gm,而后基于这组子图进行预测 f ( G ) = f ( B G ) f(G)=f(B_G) f(G)=f(BG)。具体来说,给定一个图 G G G,首先通过某种预定义的子图生成模式 π π π生成一组共享节点的子图
B G π = G 1 , … , G m , B_G^π={{G_1,…,G_m }}, BGπ=G1,…,Gm,
而后在第 l l l次迭代,有
h
G
i
,
v
(
l
+
1
)
=
f
(
h
G
i
l
,
{
{
h
G
i
,
v
l
│
v
∈
N
G
i
(
v
)
}
}
,
h
G
,
v
l
,
{
{
h
G
,
v
l
│
v
∈
N
G
i
(
v
)
}
}
)
,
h_{G_i,v}^{(l+1) }=f(h_{G_i}^l,\{\{h_{G_i,v}^l│v∈N_{G_i } (v) \}\},h_{G,v}^l,\{\{h_{G,v}^l│v∈N_{G_i } (v) \}\}),
hGi,v(l+1)=f(hGil,{{hGi,vl│v∈NGi(v)}},hG,vl,{{hG,vl│v∈NGi(v)}}),
h
G
,
v
(
l
+
1
)
=
f
(
{
{
h
G
i
(
v
)
│
i
∈
[
m
]
}
}
)
.
h_{G,v}^{(l+1) }=f(\{\{h_{G_i } (v)│i∈[m]\} \}).
hG,v(l+1)=f({{hGi(v)│i∈[m]}}).
对于子图生成模式π,作者则给出了不同的方法,包括
- 节点删除:
𝐺→所有通过从𝐺删除一个节点获得的子图 - 边删除:
𝐺→所有通过从𝐺删除一个边获得的子图 - Ego networks:
G→{ v的k跳邻居子图|v∈V(G)}
可以证明,ESAN的表达能力严格大于消息传递神经网络。
理解图神经网络的表达能力
在这一节中,我们讨论一些能够帮助我们更好地从直观上理解图神经网络表达能力的方法。
逻辑表达能力
本节主要内容取自 Pablo Barcelo et al., “The Logical Expressiveness of Graph Neural Networks”, ICLR 2020. 我们可以考虑一个逻辑表达式
α ( x ) ≔ G r e e n ( x ) ∧ ∃ y ( E ( x , y ) ∧ B l u e ( y ) ) , α(x)≔Green(x)∧∃y(E(x,y)∧Blue(y)), α(x):=Green(x)∧∃y(E(x,y)∧Blue(y)),
我们可以方便地将这种逻辑表达式应用在图中,如下图。
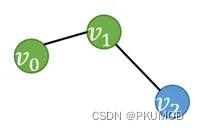
该逻辑表达式判断某个节点x是否满足如下条件:它是绿色的,同时有一个蓝色的邻居。显然,有 α ( v 0 ) = F a l s e , α ( v 1 ) = T r u e , α ( v 2 ) = F a l s e α(v_0 )=False,α(v_1 )=True,α(v_2 )=False α(v0)=False,α(v1)=True,α(v2)=False 既然逻辑表达式具有很强的可理解性,那么一个问题就是,图神经网络最多能够表达多复杂的逻辑表达式?作者在论文中的结论[11]是,对消息传递神经网络而言,它所能表达的逻辑表达式为graded modal logic[7] ,它是被如下过程递归构建的:
- φ ( x ) ≔ C o l ( x ) φ(x)≔Col(x) φ(x):=Col(x): True iff C o l Col Col 是 x x x的颜色.
- φ ( x ) ≔ φ ′ ( x ) ∧ φ ′ ′ ( x ) ∣ ¬ φ ′ ( x ) φ(x)≔φ' (x)\wedge φ'' (x) | ¬φ' (x) φ(x):=φ′(x)∧φ′′(x)∣¬φ′(x)
- φ ( x ) ≔ ∃ ≥ N ( E ( x , y ) ∧ φ ′ ( y ) ) φ(x)≔∃^{≥N} (E(x,y)∧φ' (y)) φ(x):=∃≥N(E(x,y)∧φ′(y)): True iff 集合 {u│u∈N(x),φ^’ (u)=True} 的度数至少为 N
例如,
- x 是红色,并且有一个邻居 y 连接到两个蓝色节点,可以被表达。
β ( x ) ≔ R e d ( x ) ∧ ∃ y ( E ( y , z ) ∧ ∃ ≥ 2 w ( E ( y , w ) ∧ B l u e ( w ) ) ) β(x)≔Red(x)∧∃y(E(y,z)∧∃^{≥2} w(E(y,w)∧Blue(w))) β(x):=Red(x)∧∃y(E(y,z)∧∃≥2w(E(y,w)∧Blue(w))) - x 连接到两个相邻的蓝色节点,无法被表达。
β ( x ) ≔ ∃ y z ( E ( x , y ) ∧ E ( x , z ) ∧ E ( z , y ) ∧ B l u e ( y ) ∧ B l u e ( z ) ) β(x)≔∃yz(E(x,y)∧E(x,z)∧E(z,y)∧Blue(y)∧Blue(z)) β(x):=∃yz(E(x,y)∧E(x,z)∧E(z,y)∧Blue(y)∧Blue(z))
这样,我们就可以通过逻辑表示的方法,更好地理解消息传递神经网络的表达能力。
概率推断能力
本节内容主要取自本组的工作 Tuo Xu and Lei Zou, “Rethinking and Extending the Probabilistic Inference Capacity of GNNs”, ICLR 2024. 我们可以从概率推断的角度,理解图神经网络的表达能力。
一个直观地将图以概率角度进行建模的方法是,将每个节点v的表征视作是一个未知的潜在随机变量z_v,而图中的边则表示了这些随机变量相互之间的依赖关系,即将图建模为一个马尔科夫随机场
p ( Z , X ) ∝ ∏ v ∈ V Φ v ( x v , z v ) ∏ C ∈ C Ψ C ( z C ) , p(Z,X)∝∏_{v∈V}Φ_v (x_v,z_v ) ∏_{C∈\mathcal{C}}Ψ_C (z_C ) , p(Z,X)∝v∈V∏Φv(xv,zv)C∈C∏ΨC(zC),
其中, Z = z 1 , … , z N Z={z_1,…,z_N } Z=z1,…,zN是潜在的随机变量, X = x 1 , … , x N X={x_1,…,x_N} X=x1,…,xN是节点特征, C \mathcal{C} C是图中所有(最大)团的集合。 Φ v Φ_v Φv表示节点特征 v v v与节点表示 z v z_v zv之间的关系,而 Ψ C Ψ_C ΨC表示团 C C C中节点之间节点表示的依赖关系。
有了建模方法,接下来要考虑的问题就是如何进行推断。具体来说,我们想要计算边缘分布 p ( z v ∣ X ) p(z_v |X) p(zv∣X) 来得到节点 v v v的向量表示。已有的结论是,准确推断该边缘分布通常仅仅适用于树形的图,而对于一般意义上的含有环的图,推断的复杂的过高,无法完成。一个已被广泛应用的变分推断的方法是信念广播(Belief propagation)。经验上来讲,该算法收敛时,通常我们可以得到很好的估计。既然如此,我们便提出一个问题:图神经网络是否可以模拟该变分推断过程?
我们首先考虑一个简化的分布版本:
p ( Z , X ) ∝ ∏ v ∈ V Φ v ( x v , z v ) ∏ ( u , v ) ∈ E Ψ u v ( z u , z v ) , p(Z,X)∝∏_{v∈V}Φ_v (x_v,z_v ) ∏_{(u,v)\in E}Ψ_{uv} (z_u,z_v ) , p(Z,X)∝v∈V∏Φv(xv,zv)(u,v)∈E∏Ψuv(zu,zv),
该版本中,我们只考虑边级别的依赖Ψ_uv。一个结论是,消息传递神经网络可以在这种情况下近似Belief propagation得到的结果。然而,当我们进一步考虑如下的更加复杂的分布时,消息传递神经网络便无法再次近似Belief propagation算法:
p ( Z , X ) ∝ ∏ v ∈ V Φ v ( x v , z v ) ∏ C ∈ C 3 Ψ C ( z C ) , p(Z,X)∝∏_{v∈V}Φ_v (x_v,z_v ) ∏_{C∈\mathcal{C}^3}Ψ_C (z_C ) , p(Z,X)∝v∈V∏Φv(xv,zv)C∈C3∏ΨC(zC),
其中,我们考虑所有包含至多3个节点的团。Subgraph GNNs则可以在这种情况下近似Belief propagation得到的结果。那么,我们如何继续扩展,使得图神经网络能够近似包含有任意大小团依赖的概率分布?一个简单的方法是,针对图中的每个团,额外增加一个节点,并将这个节点连接到该团中的每个节点,而后在得到的新图中再次运行消息传递神经网络。此时,每个节点的节点表示就可以完成上述的任务。
引用
- Christopher Morris, Martin Ritzert, Matthias Fey, William L Hamilton, Jan Eric Lenssen, Gaurav Rattan, and Martin Grohe. Weisfeiler and leman go neural: Higher-order graph neural networks. In Proceedings of the AAAI conference on artificial intelligence, volume 33, pp. 4602–4609, 2019.
- Christopher Morris, Gaurav Rattan, and Petra Mutzel. Weisfeiler and leman go sparse: towards scalable higher-order graph embeddings. In Proceedings of the 34th International Conference on Neural Information Processing Systems, pp. 21824–21840, 2020.
- Waiss Azizian and Marc Lelarge. Expressive power of invariant and equivariant graph neural networks. In International Conference on Learning Representations, 2021.
- Chendi Qian, Gaurav Rattan, Floris Geerts, Mathias Niepert, and Christopher Morris. Ordered subgraph aggregation networks. In Advances in Neural Information Processing Systems, 2022.
- Bohang Zhang, Shengjie Luo, Di He, and Liwei Wang. Rethinking the expressive power of gnns via graph biconnectivity. In International Conference on Learning Representations, 2023b.
- Cristian Bodnar, Fabrizio Frasca, Yuguang Wang, Nina Otter, Guido F Montufar, Pietro Lio, and Michael Bronstein. Weisfeiler and lehman go topological: Message passing simplicial networks. In International Conference on Machine Learning, pp. 1026–1037. PMLR, 2021b.
- Maarten de Rijke. A Note on graded modal logic. Studia Logica, 64(2):271–283, 2000.
- Hanjun Dai, Bo Dai, Le Song, Discriminative Embeddings of Latent Variable Models for Structured Data. ICML 2016.
- David Eppstein. Parallel recognition of series-parallel graphs. Information and Computation, 98(1):41–55, 1992.
- Keyulu Xu et al. HOW POWERFUL ARE GRAPH NEURAL NETWORKS? ICLR 2019.
- Pablo Barcel´ o et al. THE LOGICAL EXPRESSIVENESS OF GRAPH NEURAL NETWORKS. ICLR 2020.
- Tuo Xu et al. Rethinking and Extending the Probabilistic Inference Capacity of GNNs. ICLR 2024.