---

1.背景

2022年，FA Hashim等人受到蛇特殊交配行为启发，提出了蛇优化算法（Snake Optimizer, SO）。

2.算法原理

2.1算法思想

SO算法模拟蛇类的战斗与交配模式来实现全局优化。在战斗模式中，雄性为了得到最佳雌性而竞争，而每个雌性则选择最佳雄性。在交配模式中，雌雄之间交配受食物可用性影响。若交配发生在搜索阶段内，雌蛇可能产卵，孵化新后代。

2.2算法过程

初始化：
SO 算法首先生成一个均匀分布的随机群体，并假设蛇群中雌性与雄性占比均为50% ， 群体分为雄性种群和雌性种群。

SO算法寻优过程分为探索阶段和开发阶段。 其中探索阶段模拟蛇群在无食物情况下蛇类的行为模式， 开发阶段模拟食物存在时蛇类的行为模式， 蛇类行为模式通过实物总量Q和温度 Temp控制。
探索阶段：
如果Q<ThresholdQ(0.25) ， 蛇通过选择任意随机位置来寻找食物， 并更新它们的位置。 位置更新公式如下：
$$\begin{array}{rl}{X}_{i,m}\left(t+1\right)& =X_{rand,m}\left(t\right)\pm X\\ X& =c_2\times A_m\times ((X_{\max }-X_{\min })\times rand+X_{\min })\end{array}\text{\hspace{1em}(1)}$$
其中，Xi,m表示第 ｉ 只雄性位置，Xrand,m表示随机雄性的位置；Am表示雄性蛇个体的捕食能力。
开发阶段：
在 Q>ThresholdQ 时，如果 Temp>ThresholdT(0.6) ， 蛇只会向食物移动， 蛇个体的移动公式如下：
$$\begin{array}{c}{X}_{i,j}(t+1)=X_{\mathrm{food}}\pm X\\ X=c_3\times Temp\times rand\times (X_{\mathrm{food}}-X_{i,j}(t))\end{array}\text{\hspace{1em}(2)}$$
Xi,j是个体i的位置，Xfood是最佳个体的位置。
如果 Temp<ThresholdT(0.6) ， 蛇将处于战斗模式或交配模式， 蛇个体处于战斗模式下的移动公式如下：
$$\begin{gathered} X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)+X \\ X=c_3\times FM\times rand\times \left(Q\times X_{best,f}-X_{i,m}\left(t\right)\right)\text{\hspace{1em}(3)} \end{gathered}$$
Xi,m为雄性个体i的位置，Xbest,f为雌性群体中最佳位置，FM为雄性战斗力。
在 Temp<ThresholdT(0.6) 时， 蛇个体处于交配模式下的移动公式如下：
$$\begin{gathered} X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)+X \\ X=c_3\times M_m\times rand\times (Q\times X_{i,f}(t)-X_{i,m}(t))\text{\hspace{1em}(4)} \end{gathered}$$

伪代码：

3.结果展示

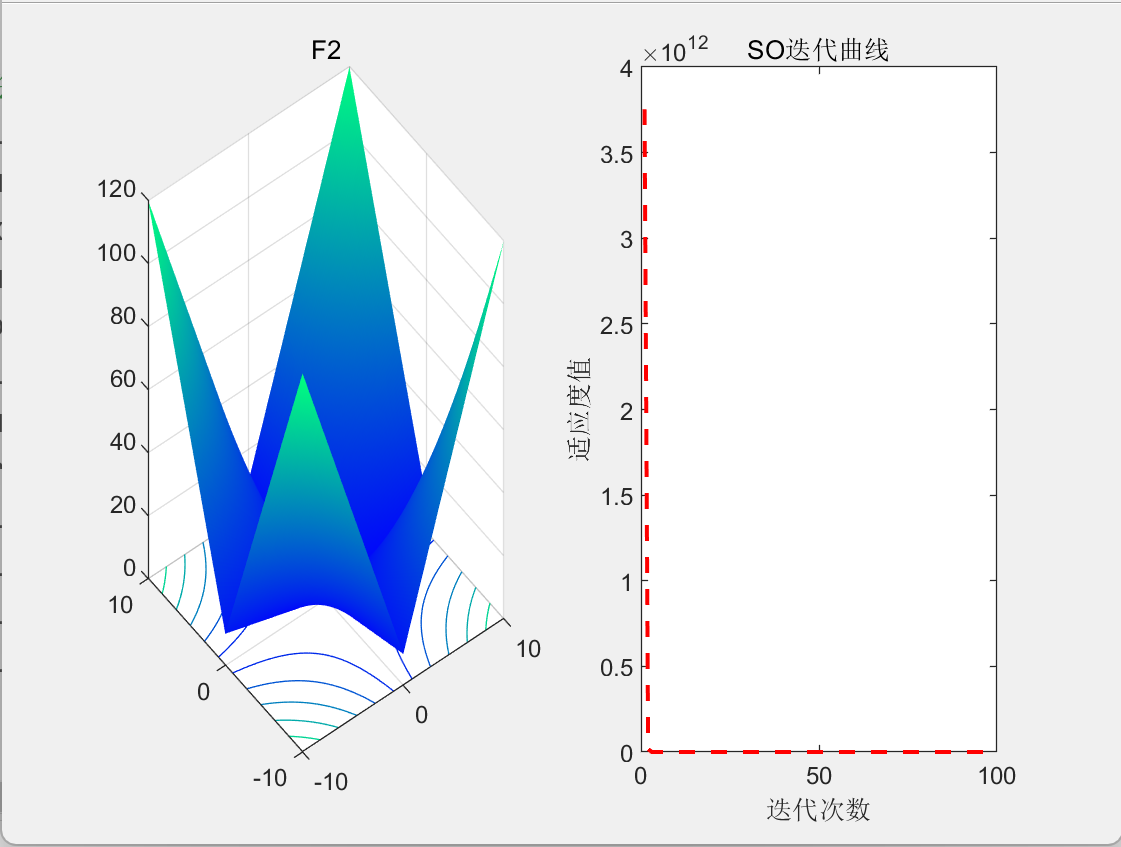
4.参考文献

[1] Hashim F A, Hussien A G. Snake Optimizer: A novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems, 2022, 242: 108320.