本题链接:PTA | 程序设计类实验辅助教学平台
题目: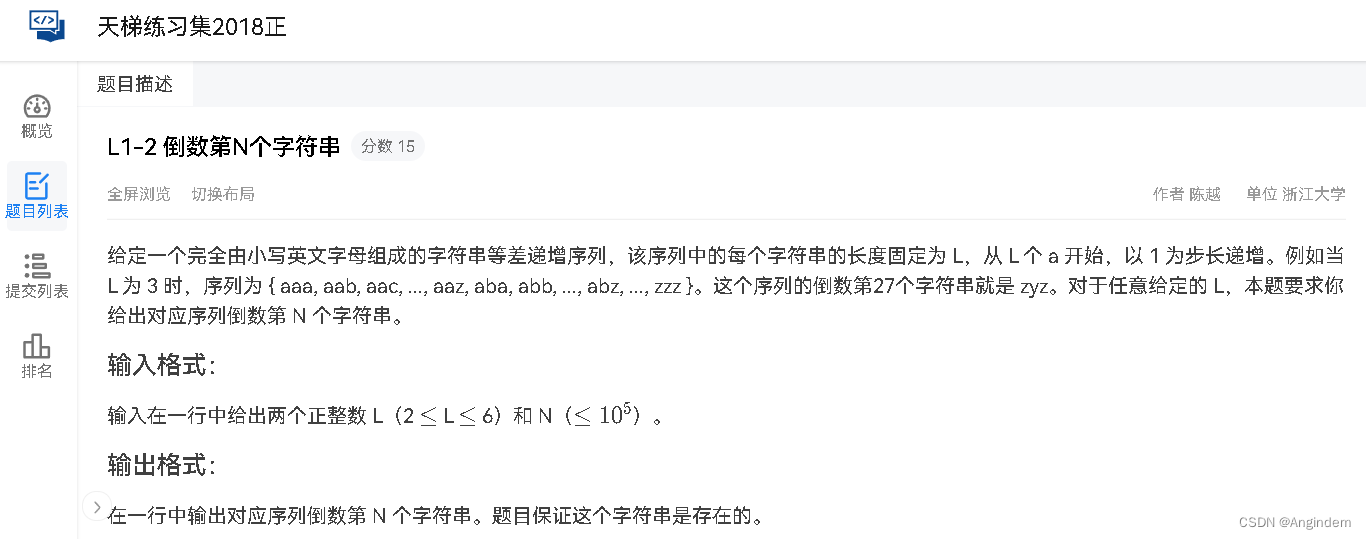
样例:
|
| pat |
思路:
根据题意,这道题是一道思维模拟题。
给出 n 位的小写字母字符串,其中进制位为 26 ,求进位+1 到 倒数第 N 个后的字符串是哪一个。
这里解决两个核心问题即可:
1、其中求 到倒数第 N 个的字符串,第几个字符串。
2、这里涉及到 高精度模拟 进位 + 1 的步骤。
1、结合排列特性,即可获得顺着的第 n 个字符串的 n 是多少:
// L 个字符串相互变化字符,实际是排列结果。
// 所以 根据排列,26个字符变化结果,L 个结果相乘,
// 即 26的 L 次幂为所有排列结果
// pow(26,L) - m 减去倒数第 N 个即可得到 顺着的 第 n 个字符串
int t = pow(26,L) - N; // 这里的 t 是用于进位用的2、参考高精度加法,高精度模拟 进位 + 1 的步骤 如下:
for(int i = 0;i < L;++i)
{
int sum = v[i] + t; // 开始相加
ans.emplace_back(sum % 26); // 相加后变化结果
t = sum / 26; // 进位 t
}
if(t) ans.emplace_back(t); // 扫尾代码详解如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
inline void solve();
signed main()
{
// freopen("a.txt", "r", stdin);
IOS;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}
int L,N;
inline void solve()
{
cin >> L >> N;
vector<int>v(L,0),ans;
// L 个字符串相互变化字符,实际是排列结果。
// 所以 根据排列,26个字符变化结果,L 个结果相乘,
// 即 26的 L 次幂为所有排列结果
// pow(26,L) - m 减去倒数第 N 个即可得到 顺着的 第 n 个字符串
int t = pow(26,L) - N; // 这里的 t 是用于进位用的
for(int i = 0;i < L;++i)
{
int sum = v[i] + t; // 开始相加
ans.emplace_back(sum % 26); // 相加后变化结果
t = sum / 26; // 进位 t
}
if(t) ans.emplace_back(t); // 扫尾
// 根据高精度加法步骤特性,倒序输出
int len = ans.size();
for(int i = len - 1;~i;--i)
{
cout << char(ans[i] + 'a');
}
}最后提交: