目录
1、星空之夜(usaco training 5.1)
2、模拟散列表(模板)
3、字符串哈希(模板)
4、四平方和(第七届蓝桥杯省赛C++ A组/B组 & JAVA B组/C组)
5、扫雷(Google Kickstart2014 Round C Problem A)
1、星空之夜(usaco training 5.1)
夜空深处,闪亮的星星以星群的形式出现在人们眼中,形态万千。
一个星群是指一组非空的在水平,垂直或对角线方向相邻的星星的集合。
一个星群不能是一个更大星群的一部分。
星群可能是相似的。
如果两个星群的形状、包含星星的数目相同,那么无论它们的朝向如何,都认为它们是相似的。
通常星群可能有 8 种朝向,如下图所示:
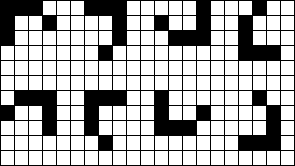
现在,我们用一个二维 01 矩阵来表示夜空,如果一个位置上的数字是 1,那么说明这个位置上有一个星星,否则这个位置上的数字应该是 0。
给定一个夜空二维矩阵,请你将其中的所有星群用小写字母进行标记,标记时相似星群用同一字母,不相似星群用不同字母。
标注星群就是指将星群中所有的 1 替换为小写字母。
输入格式
第一行包含一个整数 W,表示矩阵宽度。
第二行包含一个整数 H,表示矩阵高度。
接下来 H 行,每行包含一个长度为 W 的 01 序列,用来描述整个夜空矩阵。
输出格式
输出标记完所有星群后的二维矩阵。
用小写字母标记星群的方法很多,我们将整个输出读取为一个字符串,能够使得这个字符串字典序最小的标记方式,就是我们想要的标记方式。
输出这个标记方式标出的最终二维矩阵。
数据范围
0≤W,H≤1000
0≤ 星群数量 ≤500
0≤ 不相似星群数量 ≤26
1≤星群中星星的数量 ≤160
输入样例:
23
15
10001000000000010000000
01111100011111000101101
01000000010001000111111
00000000010101000101111
00000111010001000000000
00001001011111000000000
10000001000000000000000
00101000000111110010000
00001000000100010011111
00000001110101010100010
00000100110100010000000
00010001110111110000000
00100001110000000100000
00001000100001000100101
00000001110001000111000
输出样例:
a000a0000000000b0000000
0aaaaa000ccccc000d0dd0d
0a0000000c000c000dddddd
000000000c0b0c000d0dddd
00000eee0c000c000000000
0000e00e0ccccc000000000
b000000e000000000000000
00b0f000000ccccc00a0000
0000f000000c000c00aaaaa
0000000ddd0c0b0c0a000a0
00000b00dd0c000c0000000
000g000ddd0ccccc0000000
00g0000ddd0000000e00000
0000b000d0000f000e00e0b
0000000ddd000f000eee000
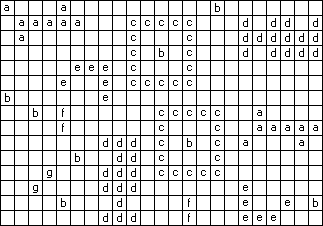
样例解释
样例对应的星空图如下:

答案对应的标记后星空图如下:
思路:
用欧几里得距离来辨别形状是否相同,用一个变量 id 来记录用到了第几个字母,top来记录连通块中点的数量,进行字母填充
代码:
//欧几里得距离
//不能保证完全不相同,但能保证大概率不相同
#include<bits/stdc++.h>
using namespace std;
const int N=101;
const double eps=1e-6;
int n,m;
typedef pair<int,int> PII;
char g[N][N];
PII q[N*N];
int top;//表示当前连通块有多少个点
double get_dis(PII a,PII b)
{
double dx=a.first - b.first;
double dy=a.second - b.second;
return sqrt(dx*dx+dy*dy);
}
double get_hash()
{
double sum=0;
for(int i=0;i<top;i++)
for(int j=i+1;j<top;j++)
{
sum+=get_dis(q[i],q[j]) ;
}
return sum;
}
char get_id(double key)
{
static double hash[30];//static 等价于全局变量 (每次调用函数,数组不会重新分配)
static char id=0;
for(int i=0;i<id;i++)
{
if(fabs(hash[i]-key)<eps)
{
return i+'a';
}
}
hash[id++]=key;
return id-1+'a';
}
void dfs(int a,int b)
{
q[top++]={a,b};
g[a][b]='0';
for(int x=a-1;x<=a+1;x++)
for(int y=b-1;y<=b+1;y++)
{
if(x==a && y==b)continue;
if(x>=0 * y>=0 && x<n && y<m && g[x][y]=='1')
{
dfs(x,y);
}
}
}//flood fill
int main()
{
cin>>m>>n;
for(int i=0;i<n;i++)
{
cin>>g[i];
}
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(g[i][j]=='1')
{
top=0;
dfs(i,j);
char c=get_id(get_hash());
//cout<<c;
for(int k=0;k<top;k++)
{
//cout<<c<<endl;
g[q[k].first][q[k].second]=c;
}
}
}
for(int i=0;i<n;i++)cout<<g[i]<<endl;
return 0;
} 2、模拟散列表(模板)
维护一个集合,支持如下几种操作:
I x,插入一个整数 x;Q x,询问整数 x 是否在集合中出现过;
现在要进行 N 次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 N,表示操作数量。
接下来 N 行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
输出格式
对于每个询问指令 Q x,输出一个询问结果,如果 x 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤N≤1e5
−1e9≤x≤1e9
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No思路:
散列表的标准写法
代码:
//1e9+7这是一个质数
#include<bits/stdc++.h>
using namespace std;
//开放寻址发一般开成两倍
//找出200000之后第一个质数
/*
for(int i=2*1e5;;i++)
{
bool flag=true;
for(int j=2;j*j<=i;j++)
{
if(i%j==0)
{
flag=false;
break;
}
}
if(flag)
{
cout<<i;
break;
}
}
*/
const int N=200003,null=0x3f3f3f3f;
//一般设最大值都是0x3f3f3f3f,大约比1e9大一些
//用null这个数表示位置上没有数字,null这个数字在题目给的数字范围之外,所以说不会引起错误
//如果设置的数在数字范围之内,可能会造成错误判断(本来没有这个数结果每个空位置都是这个数)
int h[N];
//开放寻址法
int find(int x)
{
int k=(x%N+N)%N;
while(h[k]!=null && h[k]!=x)
{
k++;
if(k==N)k=0;//后面都没有就从头开始找
}
return k;
}
void insert(int x)
{
int t=find(x);
h[t]=x;
}
int main()
{
int n;
cin>>n;
memset(h,0x3f,sizeof h);//memset是按照字节来set的,
//比如说int是四个字节,则每个字节都是0x3f,即为0x3f3f3f3f
while(n--)
{
char op[2];
int x;
cin>>op;
cin>>x;
if(*op=='I')
{
insert(x);
}
else
{
int k=find(x);
if(h[k]!=null) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
return 0;
}3、字符串哈希(模板)
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断 [l1,r1]和 [l2,r2]这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从 1 开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes思路:
字符串哈希模板写法
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
typedef unsigned long long ULL;
const int N=100010,P=131;
char str[N];
ULL h[N],p[N];
//不能映射成0
//假定不存在冲突的情况
//当p取131或1331的时候(这两个是经验值),q取成2的64次方,可以假定不会出现冲突(99.99%的情况下不会冲突)
//h[lr]=h[r]-h[l] * P**(l-r+1),为l到r之间的哈希值
//9999 - 97*100
ULL get(int l,int r)
{
return h[r]-h[l-1]*p[r-l+1];
}
int main()
{
cin>>n>>m>>str+1;
//预处理
p[0]=1;
for(int i=1;i<=n;i++)p[i]=p[i-1]*P; //每个位置的权重求出来 即为p的次方
for(int i=1;i<=n;i++)h[i]=h[i-1]*P + str[i];
while(m--)
{
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if (get(l1,r1)==get(l2,r2))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}4、四平方和(第七届蓝桥杯省赛C++ A组/B组 & JAVA B组/C组)
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多 4 个正整数的平方和。
如果把 0 包括进去,就正好可以表示为 4个数的平方和。
比如:
5=0**2+0**2+1**2+2**2
7=1**2+1**2+1**2+2**2
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对 4 个数排序:
0≤a≤b≤c≤d0
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法。
输入格式
输入一个正整数 N。
输出格式
输出4个非负整数,按从小到大排序,中间用空格分开。
数据范围
0<N<5∗1e6
输入样例:
5
输出样例:
0 0 1 2思路:
哈希加二分
代码:
//四平方和
//二分
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
struct Sum{
int s, c, d;
bool operator<(const Sum &t)const
{
if(s != t.s) return s < t.s;
if(c != t.c) return c < t.c;
return d < t.d;
}
};
int n;
Sum record[N * 2];
int main()
{
cin >> n;
int k = 0;
for(int c = 0; c * c <= n; c++)
{
for(int d = c; c * c + d * d <= n; d ++)
{
record[k++] = {c * c + d * d, c, d};
}
}
sort(record, record + k);
for(int a = 0; a * a <= n; a ++)
{
for(int b = a; a * a + b * b <= n; b++)
{
int t = n - a * a - b * b;
int l = 0, r = k - 1;
while(l < r)
{
int mid = l + r >> 1;
if(record[mid].s >= t) r = mid;
else l = mid + 1;
}
if(record[l].s == t)
{
printf("%d %d %d %d\n", a, b, record[l].c, record[l].d);
return 0;
}
}
}
return 0;
}
5、扫雷(Google Kickstart2014 Round C Problem A)
扫雷是一种计算机游戏,在 20 世纪 80 年代开始流行,并且仍然包含在某些版本的 Microsoft Windows 操作系统中。
在这个问题中,你正在一个矩形网格上玩扫雷游戏。
最初网格内的所有单元格都呈未打开状态。
其中 M 个不同的单元格中隐藏着 M 个地雷。
其他单元格内不包含地雷。
你可以单击任何单元格将其打开。
如果你点击到的单元格中包含一个地雷,那么游戏就会判定失败。
如果你点击到的单元格内不含地雷,则单元格内将显示一个 0 到 8 之间的数字(包括 0 和 8),这对应于该单元格的所有相邻单元格中包含地雷的单元格的数量。
如果两个单元格共享一个角或边,则它们是相邻单元格。
另外,如果某个单元格被打开时显示数字 0,那么它的所有相邻单元格也会以递归方式自动打开。
当所有不含地雷的单元格都被打开时,游戏就会判定胜利。
例如,网格的初始状态可能如下所示(* 表示地雷,而 c 表示第一个点击的单元格):
*..*...**.
....*.....
..c..*....
........*.
..........
被点击的单元格旁边没有地雷,因此当它被打开时显示数字 00,并且它的 88 个相邻单元也被自动打开,此过程不断继续,最终状态如下:
*..*...**.
1112*.....
00012*....
00001111*.
00000001..
此时,仍有不包含地雷的单元格(用 . 字符表示)未被打开,因此玩家必须继续点击未打开的单元格,使游戏继续进行。
你想尽快赢得游戏胜利并希望找到赢得游戏的最低点击次数。
给定网格的尺寸(N×N),输出能够获胜的最小点击次数。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 N,表示游戏网格的尺寸大小。
接下来 N 行,每行包含一个长度为 N 的字符串,字符串由 .(无雷)和 *(有雷)构成,表示游戏网格的初始状态。
输出格式
每组数据输出一个结果,每个结果占一行。
结果表示为 Case #x: y,其中 x 是组别编号(从 1 开始),y 是获胜所需的最小点击次数。
数据范围
1≤T≤100
1≤N≤300
输入样例:
2
3
..*
..*
**.
5
..*..
..*..
.*..*
.*...
.*...
输出样例:
Case #1: 2
Case #2: 8思路:
预处出每个点的数字再对0的位置进行搜索,最后对漏网之鱼进行处理
代码:
#include<bits/stdc++.h>
using namespace std;
const int N =310;
int dx[8]={1,1,1,0,0,-1,-1,-1},dy[8]={1,0,-1,1,-1,1,0,-1};
int num[N][N],st[N][N];
char g[N][N]; //记录扫雷整张地图
void bfs(int a,int b,int n) //寻找0点周围的所有点,标记为已遍历
{
st[a][b]=1;
num[a][b]=-1;
for(int i=0;i<8;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x>=0 && x<n && y>=0 && y<n)
{
if(!st[x][y] && num[x][y]!=-1)
{
if(num[x][y]>0) st[x][y]=1,num[x][y]=-1;
if(num[x][y]==0) bfs(x,y,n);
}
}
}
}
int main()
{
int T,n;
scanf("%d",&T);
for(int t=1;t<=T;t++)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%s",g[i]);
memset(num,0,sizeof num);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(g[i][j]!='*') //不是雷的要统计8个点上雷的总个数
{
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0 && x<n && y>=0 && y<n && g[x][y]=='*')
{
num[i][j]++;
}
}
}
else num[i][j]=-1; //如果是雷则标记为-1
}
}
memset(st,0,sizeof st);
int ans=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(num[i][j]==0 && !st[i][j]) //找到一个0点ans++,同时进行bfs
{
ans++;
bfs(i,j,n);
}
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
if(num[i][j]!=-1 && !st[i][j]) ans++; //找到漏网之鱼,每找到一个就ans++
}
printf("Case #%d: %d\n",t,ans);
}
return 0;
}






![[2023] 14届](https://img-blog.csdnimg.cn/direct/2fa4b80d974845d992282680c044abca.png)