题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案
提示：假设 n=5,k=3 就是需要组合出来，长度=3且内容数据是在[1,n]这个区间内的所有可能得组合
同时一个组合里面内个数字只能出现一次，[1,2,3]、[3,2,1]、[2,1,3]...等，这种只要里面的内容相同，尽管顺序不否相同都认为是同一个组合

---

题解

说实话，刚开始看到这个题，不知道怎么下手，看了看官方的题解，大概理解了思路，然后根据刚才理解的思路和自己的感觉慢慢摸索出最终的结果。
如果还有看了还不理解的同学，可以先用官方的代码打印出来一个结果，看是最终是要一个什么结果

比如我刚开始也看不明吧这个题目想干嘛，然后我尝试用官方的代码打印出来 n=5 k=3 的结果
[[1 2 3] [1 2 4] [1 2 5] [1 3 4] [1 3 5] [1 4 5] [2 3 4] [2 3 5] [2 4 5] [3 4 5]]

然后我就明白了，原来如此

开始动手写思路-思路1

虽然我已经看过了，知道要用递归，但是我在自己写的时候还是将复杂的东西拆分出来，拆成自己可以理解的，容易看懂且方便继续往下想的思路

func combine1(n int, k int) [][]int {
	// 根据题目可以确定 k 不可能大于 n
	mResult := make([][]int, 0)
	mSlice := make([]int, k)
	mIdx := 0

	// 判断当前的组合长度是否满足
	// 秉承一个条件，就是确定第一位是那个数字，后面的数字不能比第一个数字小
	// 然后就是枚举出所有可能的下一位数字的排序，一直重复这个想法

	// 当前的第一个数字确定
	mFirstNum := 1

	// 将这个数插入数组中
	mSlice[mIdx] = mFirstNum

	// 判断这个数组插入的数据是否已经满足足够的数量
	if mIdx == k-1 {
		// 满足，则将这个数组插入到结果集中
		mTempSlice := make([]int, k)
		copy(mTempSlice, mSlice)
		mResult = append(mResult, mTempSlice)
	}

	// 满足的后面就不用插入了，考虑不使用插入的最后这个数据，看是否可以继续替换别的数据继续进行

	return mResult
}

写到这里看是否合理-思路2

上面的代码片段写了后想了想，好像是可行的，既然是可行的，继续完善，当然这里我是知道最后是要用递归写的，所以后续写的思路会偏向递归的想法

func combine2(n int, k int) [][]int {
	mResult := make([][]int, 0)
	mSlice := make([]int, k)
	mIdx := 0

	// ==============================================

	// 当前使用到的数据
	mCurNum := 1
	if mCurNum > n {
		// 当前使用的数字已经超了规定，直接退出就行
	}

	if mIdx >= k {
		// 已经超过数组的长度了，后面的都不用算了，直接可以退出了
	}

	// 后续这里还可以提前预判一波，判断后面剩余的长度能否塞满数组，不能的话也没必要继续下去了

	// 这里直接将这个数插入到数组中
	mSlice[mIdx] = mCurNum
	mIdx++
	mCurNum++

	// 判断当前的数组是否刚好塞满，如果刚好塞满就可以将其插入到返回数组中
	if mIdx == k {
		mTempSlice := make([]int, k)
		copy(mTempSlice, mSlice)
		mResult = append(mResult, mTempSlice)
	} else {
		// 是如果没有塞满，继续刚才的步骤，判断数字大小、数组长度、预判后续长度是否满足 ...
	}

	// 到这里就感觉好像中间部分的数据组合还有遗漏的，上面的部分只考虑到了替换 Slice[k] 这个位置数据，
	// 前面部分都是固定的，前面可能还有很多种组合没有实现

	// 这里就要考虑一下前面部分的，比如现在是第一个数，就不要 1 这个数字插入数组
	mIdx--
	// 前面选择的数字已经自增了，这里将数组的下表调回去，然后进行上面同样的判断计算
	// 先 判断数字大小、数组长度、预判后续长度是否满足 ...

	// ==============================================

	return mResult
}

答案的雏形-思路3

到这里代码应该怎么写的雏形已经出来了，然后以及哪些参数是需要进行传递的，心里大致都会有数了，然后进行代码填充

func execFunc(aResult *[][]int, aSlice []int, aIdx, aCurNum, n int) {
	if aCurNum > n {
		return
	}

	if aIdx >= len(aSlice) {
		return
	}

	// n-aCurNum+1 假设最大值n=5 当前插入数字aCurNum=4 此时5-4+1=2 表示还有2个数(4、5)可以使用
	// 然后加上数组已经插入的个数 aIdx 如果还不够填充数组那么后面的都不会满足条件
	if n-aCurNum+1+aIdx < len(aSlice) {
		return
	}

	aSlice[aIdx] = aCurNum

	if aIdx+1 == len(aSlice) {
		mTempSlice := make([]int, len(aSlice))
		copy(mTempSlice, aSlice)
		*aResult = append(*aResult, mTempSlice)
	}

	// 如果数据还没填满，继续进行（数据填满了也会执行到这里，会在里面的判断直接退出了）
	execFunc(aResult, aSlice, aIdx+1, aCurNum+1, n)
	// 这里就考虑前面部分，假设这里没有将这个值插入到数组中，从而进行下个值的插入
	execFunc(aResult, aSlice, aIdx, aCurNum+1, n)
}

func combine3(n int, k int) [][]int {
	mResult := make([][]int, 0)
	mSlice := make([]int, k)

	execFunc(&mResult, mSlice, 0, 1, n)

	return mResult
}

到这里可以说是结束了，但是这递归方法的参数有点多，并且提交的运行结果内存占用并不是很满意，我想着官方的代码中用到了闭包，我感觉那种好像会省点内存，毕竟在go中方法的入参大部分都是值传递（可以理解为把传进来的参数复制了一份使用的）

另一种写法

在思路完全不变的情况下，使用上官方的套路看看，结果就是确实有点用

func combine4(n int, k int) [][]int {
	mResult := make([][]int, 0)
	mSlice := make([]int, k)
	var mFunc func(aIdx, aCurNum int)

	mFunc = func(aIdx, aCurNum int) {
		if aCurNum > n {
			return
		}

		if aIdx >= k {
			return
		}

		if n-aCurNum+1+aIdx < k {
			return
		}

		mSlice[aIdx] = aCurNum

		if aIdx+1 == k {
			mTempSlice := make([]int, k)
			copy(mTempSlice, mSlice)
			mResult = append(mResult, mTempSlice)
		}

		mFunc(aIdx+1, aCurNum+1)
		mFunc(aIdx, aCurNum+1)
	}

	mFunc(0, 1)

	return mResult
}

---

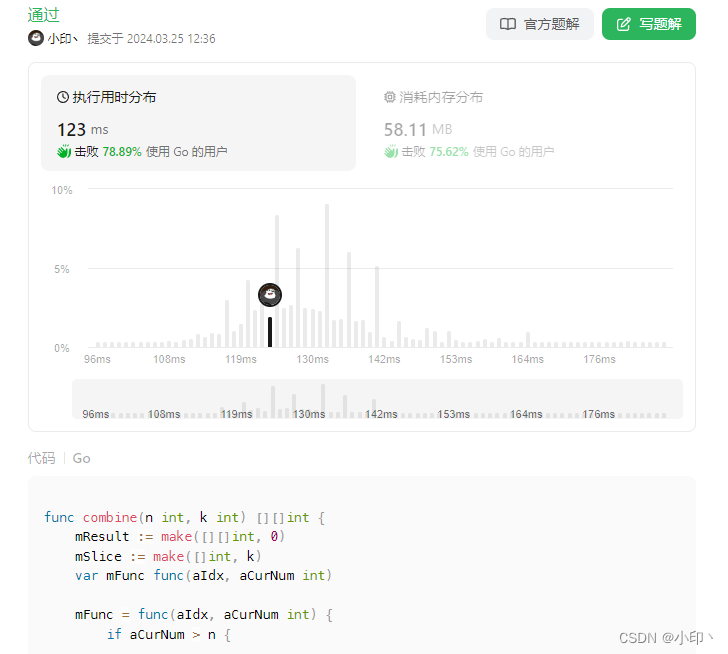
提交记录

---

题目来源：力扣题库

---

一点点笔记，以便以后翻阅。