买卖股票的最佳时机

力扣题目链接

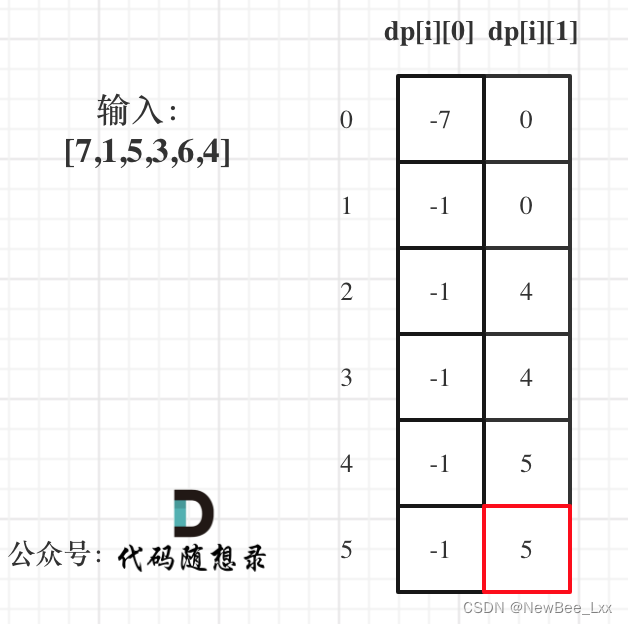
dp[i][0] 表示第i天持有股票所得最多现金 

定义二维数组 两列 ：0代表持有股票 1代表不持有股票

行代表第几天

dp[i][0] = max(dp[i - 1][0], -prices[i]);

第i天持有股票：两种情况 第一种是昨天就已经持有股票了 所以跟昨天一样就好

                                          第二种是今天买股票，以前一直没买过所以就是0-price

dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

第i天不持有股票：两种情况 第一种是昨天就没有持有股票

                                             第二种是昨天还持有股票，今天就给卖了

初始化：第0天持有股票 第0天不持有股票

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if (len == 0) return 0;
        vector<vector<int>> dp(len, vector<int>(2));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
        }
        return dp[len - 1][1];
    }
};

122.买卖股票的最佳时机II

力扣题目链接

与1不同的是可以买卖多次 但是手里最多就只能持有一个股票

解决方法不同的就是 如果第i天买入股票的时候 价值是i-1天不持有股票的钱数加上这只股票的价值

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len, vector<int>(2, 0));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[len - 1][1];
    }
};

123.买卖股票的最佳时机III

​​​​​​力扣题目链接

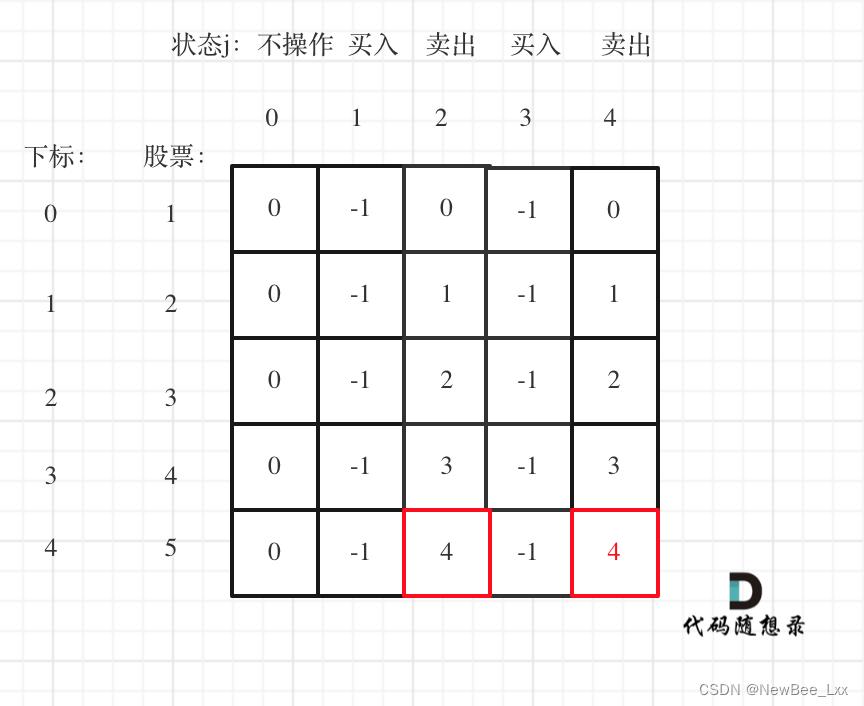
行表示 操作第几个股票

列 0 是代表不操作

     1 代表第一次持有股票

     2 表示第一次不持有股票

     3 表示第二次持有股票

     4 表示第二次不持有股票

递推公式：和前一天一样不操作

                  max（和前一天一样已经持有了第一张股票，在前一天不操作的基础上今天买入股票）

                  max（和前一天一样已经卖出了第一支股票了，在前一天持有第一支股票的基础上卖出这只股票）

                  max（和前一天一样已经持有了第二张股票，在前一天已经的卖出第一张股票的基础上买入第二张股票）

略。。。。。。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};