530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点
root,返回 树中任意两不同节点值之间的最小差值 。差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
输入:root = [4,2,6,1,3] 输出:1示例 2:
输入:root = [1,0,48,null,null,12,49] 输出:1提示:
- 树中节点的数目范围是
[2, 104]0 <= Node.val <= 105
状态:完成
思路:因为这是一个二叉搜索树,所以其中序遍历是递增的。只要中序遍历然后前一个减后一个然后跟最小值对比不断地更新最小值得出结果。
class Solution {
int preValue=0;
int min=100000;
public int getMinimumDifference(TreeNode root) {
preValue=Integer.MAX_VALUE;
mid(root);
return min;
}
public void mid(TreeNode root){
if(root==null) return;
mid(root.left);
if(Math.abs(preValue-root.val)<min){
min=Math.abs(preValue-root.val);
}
preValue=root.val;
mid(root.right);
}
}501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点
root,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
输入:root = [1,null,2,2] 输出:[2]示例 2:
输入:root = [0] 输出:[0]提示:
- 树中节点的数目在范围
[1, 104]内-105 <= Node.val <= 105
状态:完成
思路:有两种办法,第一种是暴力法,就是把所有的节点都遍历一次放到map中不用管顺序。第二种是中序遍历,中序遍历二叉搜索树是递增的,所以中序遍历时,记录上一节点的数值,如果该节点的值就是上一节点的值now++,如果不是就说明这个数字就到尽头了,然后分两种情况,第一种这个数字的个数跟最大的个数一样则收录进list中,如果这个数字个数比最大个数大则清空list并把最大个数变为该数字的个数。最后把list转为int数组。
暴力:
class Solution {
HashMap<Integer,Integer> hashMap=new HashMap<>();
public int[] findMode(TreeNode root) {
search(root);
ArrayList<Integer> list=new ArrayList<>();
int max=-100001;
for(Map.Entry<Integer,Integer> entry:hashMap.entrySet()){
int value=entry.getValue();
int num=entry.getKey();
if(max<value){
list=new ArrayList<Integer>();
max=value;
}
if(max==value) list.add(num);
}
return list.stream().mapToInt(Integer::valueOf).toArray();
}
public void search(TreeNode root){
if(root==null) return;
int value=root.val;
hashMap.merge(value,1,(oldValue,newValue)->oldValue+newValue);
search(root.left);
search(root.right);
}
}中序遍历:
class Solution {
ArrayList<Integer> list=new ArrayList<>();
int preValue=0;
int max=1;
int now=0;
public int[] findMode(TreeNode root) {
search(root);
if(now==max){
list.add(preValue);
}else if(now>max){
list.clear();
list.add(preValue);
max=now;
}
int[] result=new int[list.size()];
for(int i=0;i<list.size();i++){
result[i]=list.get(i);
}
return result;
}
public void search(TreeNode root){
if(root==null) return;
search(root.left);
if(preValue!=root.val){
if(now==max){
list.add(preValue);
}else if(now>max){
list.clear();
list.add(preValue);
max=now;
}
now=1;
}else {
now++;
}
preValue=root.val;
search(root.right);
}
}236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
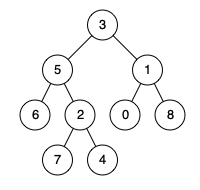
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1提示:
- 树中节点数目在范围
[2, 105]内。-109 <= Node.val <= 109- 所有
Node.val互不相同。p != qp和q均存在于给定的二叉树中。
状态:没写出来,一开始在想前序遍历找到各个目标节点的所有祖先,然后对比两个的所有祖先找到最深的哪个。
思路:使用后序遍历,当他们两个都不为空的时候就找到了最深的祖先就要一直返回这个节点。要分三种情况在后序遍历时,左节点、右节点都为空则返回空,左节点或右节点有就返回左节点或右节点,都存在则该节点就是最深的祖先节点因为是后序遍历所以肯定是最深的了。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null||root==p||root==q){
return root;
}
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left==null&&right==null){
return null;
}else if(left!=null&&right==null){
return left;
}else if(right!=null&&left==null){
return right;
}else{
return root;
}
}
}感想:今天的题目比较灵活,要熟练地掌握各个遍历地顺序并应用到题目里面去。继续学习!