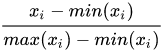🎈个人主页：豌豆射手^
🎉欢迎 👍点赞✍评论⭐收藏
🤗收录专栏：数据结构
🤝希望本文对您有所裨益，如有不足之处，欢迎在评论区提出指正，让我们共同学习、交流进步！

引言

在数据结构的世界里，顺序表是一种常见且基础的线性数据结构。它以其简洁、直观的特性，广泛应用于各类编程场景中。顺序表不仅为程序员提供了方便的数据管理方式，还在算法实现、数据处理等方面发挥着不可或缺的作用。

本文将深入剖析顺序表的定义、特性及其与数组的关系，并通过与链表的对比，展示顺序表在不同应用场景下的优势。

一 顺序表的定义与特性

数据结构中的顺序表是一种重要的线性表实现方式。下面我将详细解释顺序表的定义及其特性，以满足您的要求。

1.1 顺序表的定义

顺序表是由一组地址连续的存储单元依次存储线性表的数据元素的数据结构。

简单来说，顺序表就是将线性表的元素按照其逻辑顺序，依次存储到从计算机内存中的一段连续存储空间里。

由于这些元素的存储地址是连续的，因此我们可以通过计算元素的存储位置来快速地访问它们。

顺序表通常使用数组来实现。数组的下标与顺序表中元素的逻辑位置相对应，这使得我们可以通过数组的下标直接访问和操作顺序表中的元素。

例：

假设我们的顺序表存储的是整数元素，并且已经初始化了几个元素。下面是一个示例：

顺序表（示例）:

下标	元素值
0	5
1	10
2	15
3	20
4	25
…	…

这个表格展示了顺序表的一部分，其中下标列表示元素在顺序表中的位置（即数组的下标），元素值列表示存储在该位置的实际数据值。在这个例子中，顺序表包含从下标0到4的元素，每个元素都是一个整数。在实际应用中，顺序表的大小（即它可以存储的元素数量）是预先定义好的，并且可以根据需要进行动态调整。

请注意，这只是一个简化的示例，实际的顺序表实现会在计算机内存中占用一段连续的空间，并且通常使用编程语言中的数组数据结构来实现。此外，顺序表的大小（容量）和当前包含的元素数量（长度）也是顺序表实现中需要考虑的重要因素。

1.2 顺序表的逻辑特性

顺序表的逻辑特性主要体现在其作为线性表的一种实现方式上，具有线性表所固有的基本特性。

以下是顺序表逻辑特性的详细解释：

1. 数据元素之间具有线性关系：

   • 在顺序表中，元素之间是“一对一”的关系。这意味着除了第一个元素外，每个元素都有且仅有一个直接前驱元素；同样地，除了最后一个元素外，每个元素都有且仅有一个直接后继元素。这种关系确保了顺序表的有序性，即元素按照某种逻辑顺序排列。

2. 有序性：

   • 顺序表中的元素按照其逻辑顺序进行排列。这种顺序可以是按照元素的自然顺序（如数值大小），也可以是根据某种特定规则定义的顺序。有序性使得顺序表能够支持基于位置的访问和操作，如查找、插入和删除等。

3. 有限的元素个数：

   • 顺序表包含的元素个数是有限的。这意味着顺序表有一个固定的长度或容量，虽然在实际应用中，这个容量可以根据需要进行动态调整。有限性确保了顺序表在内存中的占用是可控的，并且可以通过索引来直接访问任意位置的元素。

4. 元素位置的唯一性：

   • 在顺序表中，每个元素的位置是唯一的。这意味着没有两个元素会占据相同的位置或索引。这种唯一性保证了顺序表操作的准确性和一致性，使得我们可以通过位置来唯一地标识和访问元素。

5. 元素的不可重复性（在某些情况下）：

   • 虽然这不是顺序表本身的固有特性，但在许多实际应用中，顺序表被用来存储不重复的元素集合。在这种情况下，顺序表中的每个元素都是唯一的，没有重复的元素出现。这种不可重复性可以通过在插入新元素时进行检查和去重操作来实现。

综上所述，顺序表的逻辑特性主要体现在其元素之间的线性关系、有序性、有限的元素个数、元素位置的唯一性以及可能的元素不可重复性。这些特性使得顺序表成为一种高效且灵活的数据结构，适用于各种需要有序访问和操作元素的场景。

1.3 顺序表的物理存储特性

顺序表的物理存储特性主要体现在其在计算机内存中的存储方式和空间占用情况。以下是顺序表物理存储特性的详细解释：

1. 连续存储空间：
   顺序表在内存中的物理存储形式是一段连续的存储空间。这意味着顺序表中的所有元素在内存中都是紧密相邻的，没有间隔。这种连续性使得顺序表在访问元素时能够快速地通过计算元素的存储位置来直接访问任意位置的元素。

2. 数组形式：
   顺序表通常使用数组的形式在计算机内存中存储。数组的下标与顺序表中元素的逻辑位置相对应，通过数组的下标可以方便地访问和操作顺序表中的元素。数组的这种特性使得顺序表在存储和访问元素时具有高效性。

3. 空间利用率高：
   由于顺序表在内存中占用连续的存储空间，因此其空间利用率相对较高。每个元素都紧密排列，没有额外的空间浪费。这使得顺序表在存储大量数据时能够有效地利用内存空间。

4. 随机访问特性：
   顺序表支持随机访问，即可以通过计算元素的存储位置来直接访问任意位置的元素。这种特性使得顺序表在需要频繁访问元素时具有较高的效率。通过元素的下标，可以直接定位到元素的存储位置，无需从头开始遍历。

需要注意的是，虽然顺序表在物理存储上具有上述优点，但也存在一些局限性。

例如，当需要频繁进行插入或删除操作时，顺序表可能需要移动大量元素以保持连续性，这会导致效率降低。

此外，顺序表在创建时需要预先分配一定的存储空间，如果分配的空间不足，则可能导致“溢出”问题；而如果分配的空间过多，则可能造成内存浪费。

综上所述，顺序表的物理存储特性主要体现在其连续存储空间、数组形式、高空间利用率以及随机访问特性等方面。

这些特性使得顺序表成为一种高效且灵活的数据结构，适用于各种需要有序访问和操作元素的场景。

总结来说，顺序表是一种通过连续存储空间存储线性表元素的数据结构，具有逻辑上的线性关系和物理存储上的连续性。这些特性使得顺序表在访问元素时具有高效率，但同时也需要注意顺序表在插入和删除元素时可能需要移动大量元素的问题。因此，在选择使用顺序表时需要根据具体的应用场景和需求进行权衡。

二 顺序表与数组的关系

数据结构中顺序表与数组的关系非常紧密，它们之间的关联主要体现在以下几个方面：

2.1 顺序表通常使用数组来实现

顺序表作为一种线性表的数据结构，其核心特性是元素之间的线性关系和在内存中的连续存储。

数组作为计算机内存中的一种基本数据结构，具有连续存储空间的特性，因此非常适合用来实现顺序表。

在实际编程中，我们通常使用数组来作为顺序表的底层存储结构，利用数组来存储顺序表中的元素。

2.2 数组是顺序表的一种具体表现形式

数组本质上是一种连续存储的数据结构，其每个元素都可以通过数组下标来访问。

当我们使用数组来实现顺序表时，数组的下标就自然地对应了顺序表中元素的逻辑位置。

因此，可以说数组是顺序表在内存中的一种具体表现形式，它使得顺序表的逻辑结构得以在物理内存中实现。

2.3 数组下标与顺序表元素的逻辑位置对应

在顺序表中，元素的逻辑位置是通过其在表中的顺序来确定的，即第一个元素位于表的开始位置，第二个元素位于第一个元素之后，以此类推。而在使用数组实现的顺序表中，这些元素的逻辑位置与数组的下标一一对应。

也就是说，顺序表中的第一个元素存储在数组的第一个位置（下标为0或1，取决于编程语言的约定），第二个元素存储在数组的第二个位置，依此类推。

2.4 通过数组下标访问和操作顺序表元素

由于数组下标与顺序表元素的逻辑位置对应，因此我们可以通过数组下标来方便地访问和操作顺序表的元素。

例如，要访问顺序表中的第i个元素，我们只需要通过数组下标i来访问数组中的对应位置即可。

同样地，对顺序表元素的插入、删除或修改等操作也可以通过修改数组对应位置的值来实现。

综上所述，顺序表与数组之间的关系是密不可分的。顺序表通常使用数组来实现，而数组则作为顺序表在内存中的具体表现形式。通过数组下标与顺序表元素逻辑位置的对应关系，我们可以方便地访问和操作顺序表的元素，从而实现各种线性表相关的操作。

三 顺序表与链表的对比

数据结构中，顺序表和链表是两种常见的线性表实现方式，它们在存储方式、访问速度以及插入与删除操作等方面存在显著差异。下面将对这些方面进行详细的对比：

3.1.存储方式：

• 顺序表使用连续的内存空间来存储元素，其内存空间在创建时就已确定，因此具有固定的长度。顺序表通过数组实现，每个元素在数组中的位置由下标决定，这种存储方式使得顺序表在物理存储上具有连续性。
• 链表则使用非连续的内存空间，通过指针连接各个节点来存储元素。链表的每个节点除了包含数据域外，还包含一个指向下一个节点的指针域。这种存储方式使得链表在内存中的分布是分散的，节点之间通过指针建立逻辑联系。

3.2 访问速度：

• 顺序表由于使用连续的内存空间，可以通过下标直接访问任意位置的元素，具有快速的随机访问能力。这种直接访问的方式使得顺序表在访问元素时具有较高的效率。
• 链表在访问元素时则需要从头节点开始逐个遍历，直到找到目标元素。这种遍历访问的方式使得链表的访问速度相对较慢，特别是在访问链表中间或尾部元素时，效率较低。

3.3 插入与删除操作：

• 顺序表在插入或删除元素时，可能需要移动大量元素以保持顺序。例如，在顺序表中插入一个元素，可能需要将插入位置后的所有元素向后移动一位；同样地，删除一个元素也需要将删除位置后的所有元素向前移动一位。这种操作在元素数量较多时，效率较低。
• 链表在插入或删除元素时，只需修改相关节点的指针即可。具体来说，插入元素时只需创建一个新节点，并修改相邻节点的指针指向；删除元素时只需找到待删除节点的前驱节点和后继节点，然后修改前驱节点的指针指向后继节点即可。这种操作方式相对简单，且时间复杂度较低。

综上所述，顺序表和链表在存储方式、访问速度和插入与删除操作等方面存在明显的差异。在实际应用中，应根据具体需求和场景选择合适的数据结构。例如，当需要频繁访问元素且元素数量固定时，顺序表可能是一个更好的选择；而当需要频繁进行插入或删除操作且元素数量不固定时，链表可能更合适。

四 顺序表的应用场景

顺序表作为一种线性数据结构，具有元素存储连续、可以通过下标直接访问元素的特性，因此适用于多种应用场景。以下是一些具体的使用场景，结合要求进行介绍：

4.1. 需要频繁访问元素且元素个数相对固定的场景

• 学生成绩管理：在学生成绩管理系统中，通常需要存储每个学生的成绩信息，并且需要频繁地查询、修改或统计这些成绩。由于学生人数在一段时间内是固定的，因此使用顺序表来存储成绩信息是一个合适的选择。通过顺序表的下标，可以快速地定位到某个学生的成绩记录，进行读取或修改操作。
• 图书借阅记录：图书馆需要记录每本书的借阅情况，包括借阅人、借阅时间等信息。由于图书的数量是有限的，并且需要频繁地查询某本书的借阅状态，顺序表同样是一个合适的数据结构。通过顺序表，图书馆可以快速定位到某本书的借阅记录，进行借阅状态的更新或查询。

4.2 内存空间充足且需要快速访问元素的场景

• 数组排序：在排序算法中，经常需要对数组中的元素进行排序。由于排序过程中需要频繁地访问和比较数组中的元素，因此使用顺序表作为底层数据结构是非常合适的。顺序表能够提供快速的随机访问能力，使得排序算法能够高效地执行。
• 查找算法：在查找算法中，如线性查找、二分查找等，也需要频繁地访问数组中的元素。顺序表作为数组的一种表现形式，同样适用于这些查找算法。通过顺序表的下标，可以快速定位到待查找的元素位置，并进行比较和判断。

在这些场景中，顺序表的优势在于其元素存储的连续性和直接访问能力。由于元素在内存中是连续存储的，顺序表可以充分利用CPU的缓存机制，提高数据访问的速度。同时，通过下标直接访问元素的方式，可以避免链表等数据结构在访问元素时可能产生的额外开销。

需要注意的是，虽然顺序表在这些场景中表现出色，但并不意味着它适用于所有情况。例如，在需要频繁进行插入或删除操作且元素个数不固定的场景中，链表可能是一个更好的选择。因此，在选择数据结构时，需要根据具体的应用场景和需求进行权衡和选择。

总结

通过对顺序表的深入剖析，我们不难发现，它以其独特的逻辑特性和物理存储方式，在数据处理中发挥着举足轻重的作用。

与数组紧密相连的关系，使得顺序表在内存管理、元素访问等方面具有高效性。与链表的对比则进一步凸显了顺序表在特定场景下的优势。无论是需要频繁访问元素的场景，还是内存空间充足的情境，顺序表都能展现出其独特的魅力。

因此，在实际编程中，我们应根据具体需求，合理选择并应用顺序表这一数据结构，以优化程序性能，提高数据处理的效率。

这篇文章到这里就结束了

谢谢大家的阅读！

如果觉得这篇博客对你有用的话，别忘记三连哦。

我是豌豆射手^，让我们我们下次再见