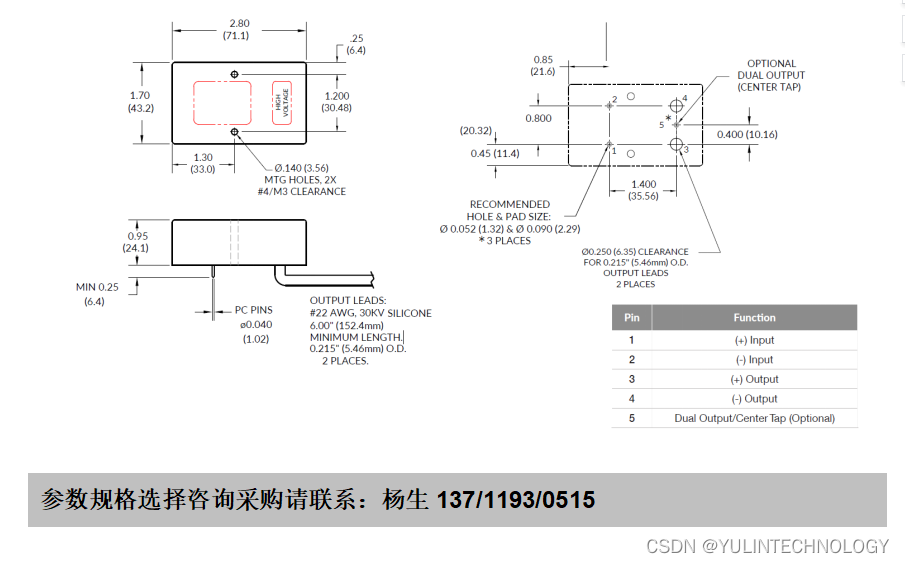
1.硬件接线

        电源3.3v~5v;

      一个触发信号，3.3伏20us的脉冲。

     一个接收，为脉冲的宽度，也就是高电平时间。

2.距离计算

         距离=音速x时间/2；  D=340m/s *Th /2,Th:为高电平时间。

        距离范围：2~400cm

       代码比较简单，就是给一个触发信号，然后接收引脚回你一个与距离成线性关系的变宽脉冲。

3.数据跳变问题

       限幅滤波滤除那些超过量程范围的，大于23.5ms（也就是计算长度大于400cm）的数据全部丢弃。

      卡尔曼滤波让曲线变平滑，一维卡尔曼，只是对采集的时间滤一下波。

      

float x=0;//当前估计值
float last_x;//上一次估计值
float last_p;//上一次预测误差
float p=1;//预测误差
float q=0.01;//环境噪声，这个一般选择0.2
float r=0.2;//预测噪声，决定了曲线的平滑程度，曲线越平滑，越耗费时间资源
float k=0;//卡尔曼增益

//参数z表示实测值
float kml(int z){
  last_x=x+0;//获得上一次估计值
  last_p=p+q;//获得上一次预测误差
  k=last_p/(last_p+r);//求得卡尔曼增益
  x=last_x+k*(z-last_x);//求得估计值
  p=last_p-k*last_p;//更新预测误差
return x;//返回滤波获得值
}

    多维的就会涉及到协方差，协方差是两个属性的相关性。 

测试：

main循环时间：1ms	无滤波：值	卡尔曼：值
1	0	0
2	6	5
3		5.5
4		5.8
5		6

               他不会一下子就达到目标值，而是慢慢到达目标值。而这个慢慢就是滤除干扰和突变。

 本质：将数据突变变得更平滑，但是需要更多的时间。换个思路就是我干的多，我会按照趋势变化，但是变化需要更多的时间资源。预测噪声变大，曲线更平滑，需要更多的时间资源。

4.优劣

     滤波之后，数据变得更平滑，对数据干扰突变的抵抗性增强，基本不受异常信号影响，但是对实时性要求比较高的状态下很不理想，测不出来那种一闪而过的物体距离。适合动作姿态变化，因为动作姿态不会突变。