目录
1 树的概念及结构
1.1 树的结构
1.2 树的概念
1.3树的表示
2 二叉树的概念及结构
2.1二叉树的概念
2.2 特殊的二叉树
2.3 二叉树的存储结构
1 树的概念及结构
1.1 树的结构
前面所学到的顺序表链表等,都是线性的数据结构,今天介绍的树,是一种非线性的数据结构,因为它看起来像一棵倒挂的树,所以这种结构被称为树。

在树形结构中,树的子集之间是不能有交集的,也就是子集中的交点不能相交。

这种结构不是树,因为子树之间有相交。
1.2 树的概念

以这张图为例:
节点的度:每个节点的子节点数目被称为度,如A的度为6.
叶节点或终端节点:度为0的节点被称为叶节点,也就是终端节点,如B,C, H, I。
非终端节点或分支节点:度不为0的节点被称为非终端节点,如D,E,F G。
双亲节点或父节点:该节点的上一个节点被称为双亲结点,一般为了简易称父节点,如B,C,D,E的父节点都是A。
孩子节点或子节点:同父节点,父节点的孩子的节点被称为子节点,如H是D的子节点。
兄弟节点:父节点相同的两个或多个节点之间被称为兄弟节点,如K,L,M是兄弟节点。
树的度:一棵树的度是所有节点中最大的度,如A的度是6,是所有节点里面最大的,所以树的度为6。
节点的层次:从根开始为第一层,往下一个节点层数加一,一般默认根为第一层(可以从第0层开始)。
树的高度或者深度:层次的最大值就是树的高度。
堂兄弟节点:父节点在同一层的节点是堂兄弟节点,如H 和 I 。
节点的祖先:从该节点的线路一直往上遍历,所有的节点都是该节点的祖先,如A是所有节点的祖先。
子孙:某节点之下的所有子树的节点都是该节点的子孙。
森林:互不相交的n棵树(n >=2)组成的集合叫做森林。
1.3树的表示
树有许多种表示方法,不同于顺序表链表,它常用的表示方法有孩子兄弟表示法。
//孩子兄弟表示法
struct Tree
{
struct Tree* child;
struct Tree* Brother;
int val;
};
如上。
树的表示方法有许多种,我们可以根据实际情况进行选取。
树的应用穿插在我们身边,如电脑中的文件,打开一个会有子文件,这就是树的应用。
2 二叉树的概念及结构
2.1二叉树的概念
倘若我们学习节点很多且不确定数量的树,难度是十分大的,所以为了便于理解,我们学习二叉树:
二叉树顾名思义,至多有两个节点的树状结构就是二叉树,同理,N叉树就是节点至多有N个的树状结构。

结合树的概念,我们知道二叉树的子树可以分为左子树和右子树,并且度不能超过2,二叉树实际上就是由空节点,根节点,左子树,右子树,左右子树均存在复合而成的。
2.2 特殊的二叉树
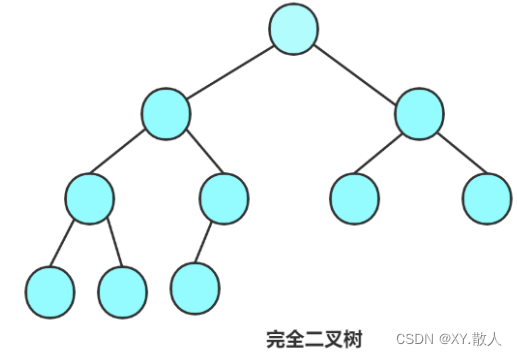
特殊的二叉树分为完全二叉树和满二叉树。
满二叉树:满二叉树除了最后一层的节点度全为0,其余节点的度都是2。
完全二叉树:完全二叉树可以说是特殊的满二叉树,完全二叉树在满二叉树的基础上允许倒数第二层的节点的度不全为0,但是最后一层从左到右的节点必须挨着。
2.3 二叉树的存储结构
二叉树存储分为顺序存储和链式存储,这里有个问题:二叉树相对于顺序表和链表的优势在哪里?
实际上,如果我们只是为了存储数据,二叉树的价值是远远不如顺序表和链表的,存储数据多简单,顺序表链表轻松搞定。
二叉树的优势是在于搜索,存储只是一方面,搜索方面二叉树才是强项,如后面介绍的,AVL树,红黑树等。
二叉树的物理结构是数组,逻辑结构是二叉树,真正实现的时候存储数据也是用数组存储的。
所以下一篇介绍的就是二叉树的顺序存储,称为堆,这个堆是数据结构的堆,而不是操作系统的堆。
感谢阅读!

![[音视频学习笔记]八、FFMpeg结构体分析 -上一个项目用到的数据结构简单解析:AVFrame、AVFormatContext、AVCodecContext](https://img-blog.csdn.net/20130914204051125?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvbGVpeGlhb2h1YTEwMjA=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)