前言：

本篇博客主要介绍有关栈和队列数据结构相关知识

思维导图介绍：

开始之前，先介绍一下这篇博客主要介绍的主体内容：

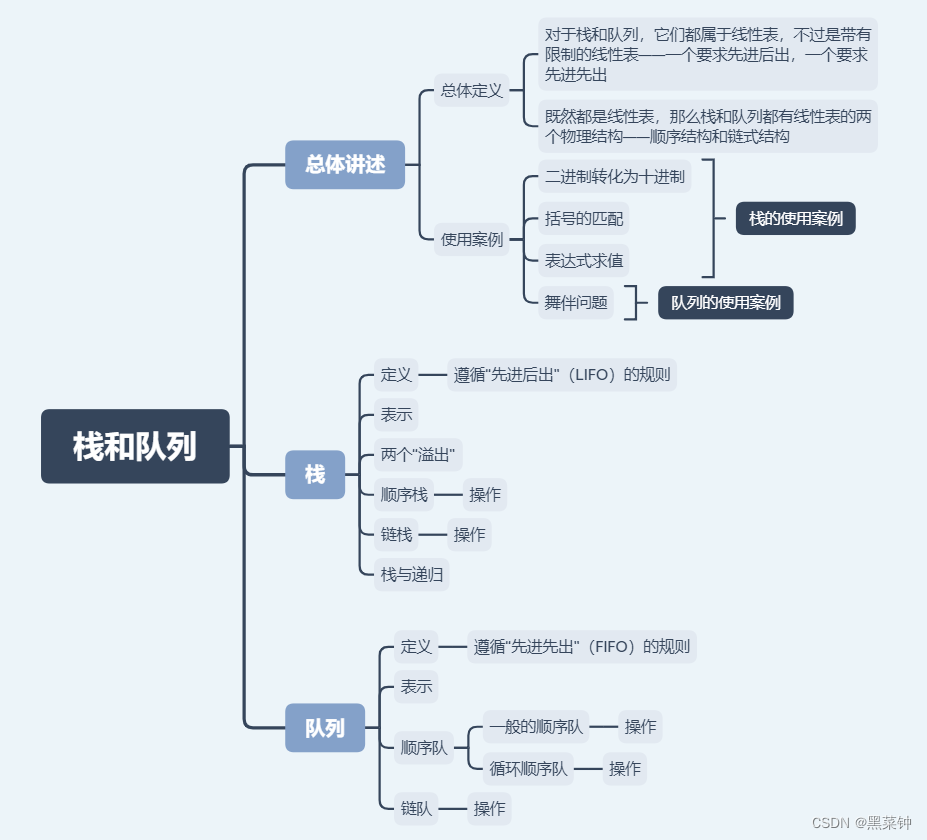
栈和队列：

回顾线性表：

在刚才的思维导图里我们也了解到了——栈和队列都属于线性表，那么这里复习一下什么是线性表呢？

线性表——根据数据结构的分类来讲——

1.对于它的逻辑结构而言——它是线性结构

2.而它的物理结构有两种——顺序存储结构和链式存储结构

它通俗的来讲就是把数据按顺序存储在内存中的一种数据结构

那现在就让我们进入正题吧——

基本定义：

栈和队列都属于一种限制出入的线性表，不过它们所限制的方式不同

栈属于限制线性表先进入到表里的最后才可以获取到——也就是“先进后出”，类比装在弹夹里的子弹，先装进去的最后才打出来。

队列是限制——一端是进入表中的，一端是出表的，讲究"先进先出"的规则，这个其实可以类比排队的 ，先排队的总是可以先进行活动，而一端来人，一端出人。

使用案例：

进制转换

这里的主要是在十进制转化为其余进制而使用的——对于十进制转化为二、八、十六进制，它们都有一个基本的共识——除R取余（这里的R指转化成进制的2、8、16）

而对于这个取余，我们一般都是倒着取，也就是——先除R得到的那个余数在最后一位。

这个很明显的符合我们刚才介绍的栈的特性——先进后出。

因此栈可以在这个进制转换中使用，具体使用方法等介绍完栈的知识再做讲解

括号的匹配

假如给你几个括号，让你判断它们是否都配对成功了。

例如：{([])}这个就是配对成功了，{)[(}而这个显然不是

那么如何解决这一道题目呢——使用栈

这里先基本介绍一下使用方法——

先把一半的括号插入到栈中，然后再插另一半，插一个的时候要判断，是否和栈中的括号匹配，如果不匹配就直接报错，如果匹配则对应的括号出栈，直到所有元素出栈则可以说明所有的括号都匹配成功

表达式求值

对于一个简单的表达式，由于符号的优先级不同，则运算数据也不同，而利用表达式求值可以使用栈的方法，这个设计的算法比较复杂，在讲解完栈后再讲解。

舞伴问题

假如要你要开办一个舞会，舞会上让男女配对跳舞，则男生和女生站两列，她们位置一致则匹配成功，排在前面的，就先和对应的搭档开始跳舞，如果有一对的人比较多，配对不成，则他就成为下一首歌的第一个和异性匹配并跳舞的人。

栈（stack）：

定义：

具有先进后出限制的线性表。

有顺序栈和链栈两种形式。

创建栈：

顺序栈的创建——

设置一个结构体，里面存放两个指针——一个指向栈顶，一个指向栈尾。和一个数组大小

构建基本代码：

typedef struct {
    Stackelem *top;
    Stackelem *base;
    int stacksize;
}Sqstack;

注意这里的Stackelem是指放在栈中的元素类型 

两种溢出形式

对于栈而言，有两种溢出形式：

一般而言上溢出只发生在顺序栈中，而链栈由于可以自己手动分配空间，基本不存在上溢出的问题。

1.上溢出，入栈元素过多，超过栈的最大空间，则发生错误，上溢出。

2.下溢出，一直出栈，但是栈里已经没有元素了，因此发生错误，下溢出。

但是，一般把上溢出看为错误，而把下溢出看为一种结束条件

满栈和空栈：

那么如何判断这个栈是否满？或者是否为空？

这里画一个图：

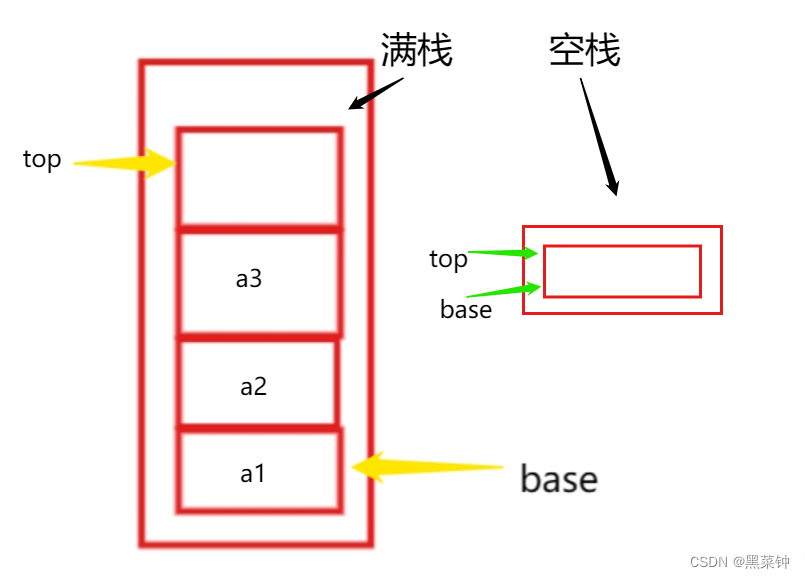
如图所示，这是一个基本的顺序栈，而在这个栈中，初始状态——也就是base和top指向第一个位置，这时候栈内为空，而当top所指向的空间是开辟空间最后一个了，那么栈满了。

那现在理论解释明白了，代码该怎么表示呢？

——

对于栈空：当top==base时栈为空

对于栈满：当top-base==stacksize时栈满

栈空和栈满在下面的一些基本操作中也会用到，所以这里先提前介绍一下如何判断栈空或是栈满的情况。

顺序栈

基本操作：

初始化

初始化就是先开辟一块大小确定的空间，然后base指针指向这块空间，判断是否开辟成功，如果空间开辟失败，则错误退出，如果开辟成功，则让top指针=base指针，让stacksize等于开辟空间的大小

代码：

int initstack(Sqstack& s)
{
	s.base = new int[MAXSIZE];//c++开辟新空间的语句，利用new开辟，相当于c语言中的malloc
	if (s.base)
	{
		return -1;
	}
	s.top = s.base;
	s.size = MAXSIZE;
	return 0;
}

销毁栈

销毁栈，就是需要把栈所占的空间给释放掉，而刚开始开辟的时候是动态开辟，这里就用到delete关键字，这个关键字作用和c语言中的free一样，都是释放掉动态开辟的内存，直接delete base，然后把top和base指针置空，栈长=0即可。

代码：

Status Destorystack (SqStack &s)

{

        if(s.base)

        {

        delete s.base;

        s.stacksize=0;

        s.base=s.top=NULL;

        }

        return OK;

}

置空栈

把栈中元素置空，而不管空间的事，这个操作就直接让top=base即可，这样top和base之间的元素为0，置空栈操作成功

Status ClearStack(SqStack s)

{

        if(s.base)

        {

         s.top=s.base;

        }

        return OK;

};

入栈

假如栈为空则——入栈就是先把top指针的位置给赋值成传进来的值，然后把top指针往上移一位。

 Status Push(Sqstack &s,Stackelem e)

{

       if(s.top-s.base==s.stacksize)

                return ERROR;

        *s.top=e;

        s.top++;

        return 0;

}

出栈

设定一个变量，把top下面位置存放的数据赋值给这个变量，然后top指向这个位置即可

 Status Push(Sqstack &s,Stackelem e)

{

       if(s==NULL)

                return ERROR;

        e=s.--top;

        return 0;

}

判断是否为空

上面已经介绍了如何判断栈是否为空了，就是当top和base相等时栈为空。

代码：

Status  Stackempty(SqStack s)

{

        if(s.top==s.base)

         {

                return true;

        }else{

                return false;

        }

}

链栈

构建：

链栈和顺序栈的最大区别就是物理结构不同，顺序栈用到了c++中的数列，而链栈要用到前面的链表，在链表中存放数据和指针。

这意味之前的结构体构建到这里不能用了，因此这里介绍一下新的构建：

结构体里要包含数据域和指针域

typedef struct StackNode

{

        stackelem data;

        struct StackNode *nextl

}StackNode,*LinkStack;

LinkStack s;//s代表指向结构体类型变量的指针

 

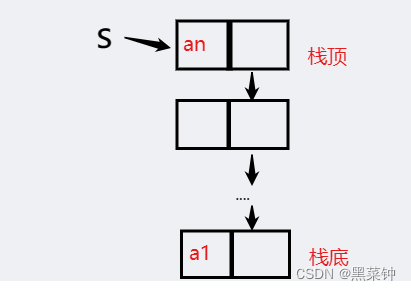
🎄注意：链表的头指针就是栈顶，这个链栈没有头结点，而这个一般不会溢出——出现栈满的情况。

基本操作：

初始化：

Status InitStack(LinkStack &s)

{

        s=NULL;

        return OK;

}

对于链栈的初始化就和顺序栈的有很大区别了，向初始化函数传入头指针，让头指针置为空，即头指针=NULL即可——这里会有人问了，为什么让头指针置为空？不应该是让指针所指的next(指针域)为空吗？

其实，这里要注意一点——链栈的链表没有头结点

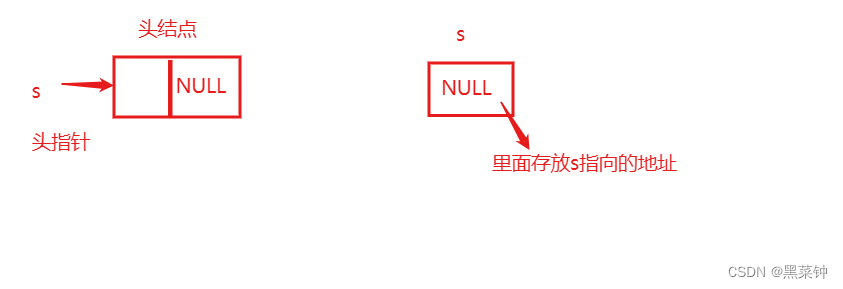
🎄头指针和头结点不一样，头结点初始化是要把头结点的next域置为空，而头指针是直接把自己=NULL，置为空，因为指针所占用的空间是存储所指的位置的，指针位置置为空，则对于这个链栈的初始化来说——完成。

入栈

入栈就是先开辟一块空间，空间类型为自建的结构体类型，然后让这块空间的指针域指向头指针所指向的空间，然后让头指针指向新开辟的空间——这样就可以只借助一个头指针来完成栈的操作了

 Status Push(LinkStack &s,stackelem e)

{

        LinkStack a=new StackNode;

        a->data=e;

        a->next=s;

        s=a;

        return OK;

}

出栈

出栈就是先提取出来要出栈的数据域的值，然后让头指针指向出栈的下一个，最后释放掉出栈的空间。

Status Pop(LinkStack &s)

{

       if(s=NULL){

                return ERROR;

        }

        e=s->data;

        p=s;

        s=p->next;

        delete p;

        return OK;

}

队列（queue）：

定义：

队列是一种限制进出的线性表，“先进先出”（FIFO），在生活中这个性质比较常见些，比如排队买饭……

而队列是限制一端进，一端出，每一端都有不同的操作。

常见应用：

• 多用户系统中，多用户排队，按照来的顺序来循环使用CPU和主存。
• 按照用户的优先级拍成多个队，每个优先级一个队列
• 实时控制系统，信号按照接受的先后依次处理。
• 网络电文传输，按照到达的实践依次进行
• ……

顺序队列

构建表示：

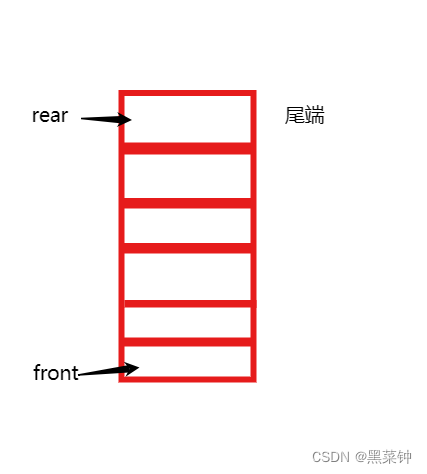
上图就展示了一个队列拥有的基本特征，其中的rear是指向队尾，front是指向队头。

rear端进行进入队列操作，而front端进行出队列操作，所以这里可以引入——如何判断队列为空：

当front和rear指向同一位置时，队列为空。

 那顺序队列的类型构建该怎么构建呢？

示例代码如下：

#define MAXQSIZE 100
typedef struct{
    QElemType *base;//动态分配存储空间
    int rear;
    int front;
}SQueue;

这里写的的rear尾指针和front头指针为int类型，这时候会有些疑惑——不是说这个它们是指针吗？怎么写成整型的形式？

这是因为这里顺序队列所借指的是数组，而且不是动态分配的数组？所以数组的下标和指针有着一样的作用，则可用整型代表更安全。

一般顺序队列

操作：

初始化：

初始化顺序队列，就是把头指针和尾指针指向初始位置即可

代码如下：

Status  InitQueue (SQueue &q)

{

       q.base=new  QElemType[MAXQSIZE];//这里的QElemType是指所队列存放数据的类型，按需求填入不同数据类型。

        if(!q.base)        exit(-1);

        q.front=q.rear=0;

        return OK；

}

入队： 

入队，就是让入队的数据赋值给rear指针指向的区域，再让指针++

即：

q.base[rear]=x;

q.rear++;

出队：  

先把front指针指向的空间存储数据赋值给某个变量，再把front头指针往上移动一位即可

简易代码：

e=q.base[q.front];

q.front++;

注意当front==rear时队列为空，不能再出队。

❀BUT

当我们执行这些操作直到队列满，在空间内，我们发现还有一些空间没有利用，这块空间是出队列时front往上移动而产生的结果，那这块空间我们能不能再利用呢？就像排队一样，排完队的人出队后，后面的人就会自动往前补上。

答案是——当然可以。

下面就介绍队列中比较常用的顺序队列——循环队列

循环队列

这个队列的设置是为了解决假上溢出的较好的方法，那什么是假上溢呢？其实刚才就提到了——当出队后使头指针下的位置为空，而队列内——即头指针和尾指针之间的位置已经满了，如果再入队则会导致溢出，BUT这种溢出被称为假溢出，因为所开辟的空间内还有未用的存储单元，所以解决办法就是循环队列——

将队列设想为一个循环的表：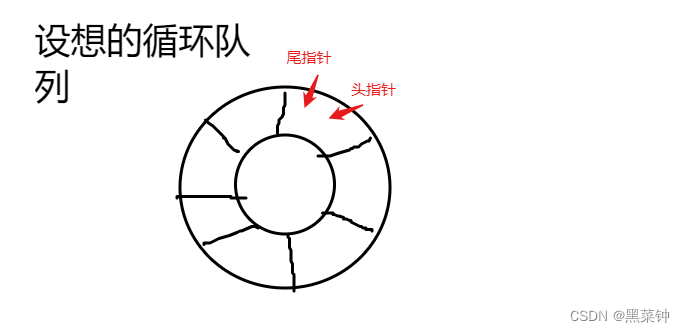

在这样一个表中可以重复利用开辟的存储空间，当rear=maxqsize时，假如开始端空着，则可以从头利用空间，而当front=maxqsize时也可以如此，这便称为循环队列

操作：

那如何实现这循环队列呢？即当rear+1=maxqsize ，则令rear=0;

——

利用取余符号%来实现一个圈的循环

让rear=rear%maxqsize，当rear<maxqsize时rear仍=rear,当rear=maxqsize时rear=0

同理front也是。

插入元素：

那循环队列如何插入元素？

q.base[q.rear]=x;//x是插入的元素

q.rear=(q.rear+1)%MAXQSIZE

//注意：这里＋1的原因是插入元素后，rear需要往上移动一位

删除元素：

e=q.base[q.front];

q.front=(q.front+1)%MAXQSIZE

//这里的+1的原因如上。

队空：

如何判断循环队列为空？

q.rear==q.front

队满：

那如何判断队满呢？

思考一下发现队满也是q.rear==q.front

那如何区分所谓的队空和队满呢？

方法如下：

• 1.把循环队列空出一格出来，意思是少用一个元素空间
• 2.设置一个变量，记录元素的个数来判断区分队满和队空
• 3.设置一个标志区分队空和队满

而最常用的就是少用一块空间，

这样：

当空队时front==rear

当队满时（rear+1）%MAXQSIZE==front

那这个式子为什么用%符号了？——因为循环队列，不清楚到底rear大还是front大，rear指向队列中空出的区域，当rear+1就是可能和front相等，也可能和front差一个MAXQSIZE，那用取余符号列出的式子就可以概括这两种情况，完成判断队满的操作了。

具体的操作：

初始化：

Status  InitQueue (SQueue &q)

{

       q.base=new  QElemType[MAXQSIZE];//这里的QElemType是指所队列存放数据的类型，按需求填入不同数据类型。

        if(!q.base)        exit(-1);

        q.front=q.rear=0;

return OK;

}

 求队列长度：

int LengthQueue(SQueue q)

{

        return ((q.rear-q.front+MAXQSIZE)%MAXQSIZE);

}

这个式子其实有点难理解，下面就进行具体的讲解一下这个式子到底怎么得出的

——

这里列举以下几种情况

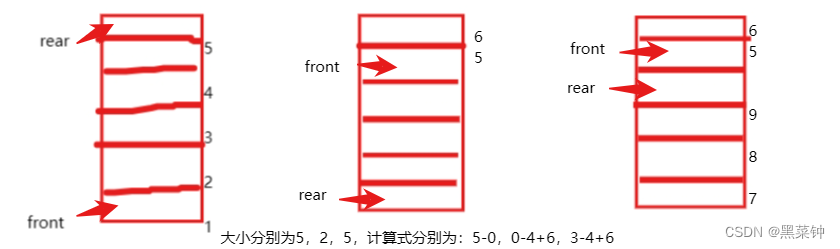
如上图，我们列出了它们分别的计算式和结果，计算式的本质式分别为：rear-front,rear-front+Maxqsize,rear-front+Maxqsize

那么现在是想怎么把这两个式子合为一个——取余符号

即rear-front+MAXQSIZE再整体取余MAXQSIZE

入队：

Status EnQueue (SQueue &q,QElemType e)

{

if((q.rear+1)%MAXQSIZE==q.front)

        return ERROR;

q.base[q.rear]=e;

q.rear=(q.rear+1)%MAXQSIZE;

return OK;

}

出队：

Status OutQueue (SQueue &q,QElemType x)

{

if(q.rear+1==q.front)

        return ERROR;

x=q.base[q.front];

q.front=(q.front+1)%MAXQSIZE;

return OK;

}

链队

基本操作：

链队即使用数据结构中的物理结构——链式结构来实现队列的一个数据结构

注意：front为头指针，它指向头结点，而头结点中没有data数据域。

类型定义：

#define MAXQSIZE 100

typedef  struct Qnode{

        QElemType data;

        struct Qnode*next;

}Qnode,*Queueptr;

typedef struct 
{

        Queueptr front;

        Queueptr rear;

}LinkQueue;

初始化链队：

传入LinkQueue自定义类型，并动态开辟一块空间，空间类型为Qnode。front和rear指向同一块空间

Status InitListQueue(LinkQueue &q)

{

        q.front=q.rear=new QNode;

        q.front->next=NULL;

        return OK;

}

入队：

Status InQueue(LinkQueue &q,ElemType e)

{

        LinkQueue s=new QNode;

        s->data=e;

        s->next=NULL;

        q.rear->next=s;

        q.rear=s;

        return OK;

}

出队：

Status OutQueue(LinkQueue &q,ElemType x)

{

       if(q.front==q.rear)        return ERROR;

        p=q.front->next;

        x=p->data;

        front->next=p->next;

        if(q.rear==p)        q.rear=q.front;

        delete p;

        return OK;

}

销毁： 

Status DeleteQueue(LinkQueue &q)

{

        while(q.front)

        {

                p=q.front->next;

                delete q.front;

                q.front=p;

         }

}

总结：

好了，到这里，栈和队列的知识就介绍完毕，欢迎点赞收藏，或者关注专栏，以免找不到哦🤭

文章如有问题，可以私信或者评论区留言，感谢观看完毕o(*￣▽￣*)ブ