个人主页 : zxctscl
如有转载请先通知
题目
- 1. 91.解码方法
- 1.1 分析
- 1.2 代码
- 2. 62.不同路径
- 2.1 分析
- 2.2 代码
- 3. 63.不同路径 II
- 3.1 分析
- 3.2 代码
1. 91.解码方法

1.1 分析
题目所述就是把一串数字反向解码为字母映射出来,有多少种方法。
题目也说,一个单独的数字可以映射的,但是这个数字前面是0的话就不可以。
来看看题目给的示例:
226就有三种解码方式:它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6)

- 以i位置,要求的就是以i位置结尾方法的总数;
- 状态表示方程:来找解码到i位置时最近的一步,可以分成两种情况:(1)i这个位置单独解码;(2)i位置和i-1结合一起共同解码。这两种情况都会出现解码失败和成功的情况。
(1)以i位置单独解码,如果这个数字在1-9之间,就能成功也就是有dp[i-1]种;如果失败就是0;
(2)i位置和i-1结合一起共同解码,如果这两个数字结合在10-26之间,就解码成功,所以解码成功就是dp[i-2],;解码失败就是0。
状态表示方程:dp[i]=dp[i-1]+dp[i-2],都是成功时候才加。 - 初始化,要把0位置和1位置。以0位置结尾说明就只有一个字符,在1-9之间就成功就是1,如果失败就是0。以1位置进位有三种情况:(1)两个字符都可以单独解码;(2)两个字母合在一起解码成功;(3)前面两种都不存在。它的解码数可能是0,1或者2。
- 填表顺序:从左往右
- 返回值:这个字符串的解码方式,也就是到字符串i-1位置:dp[i-1]
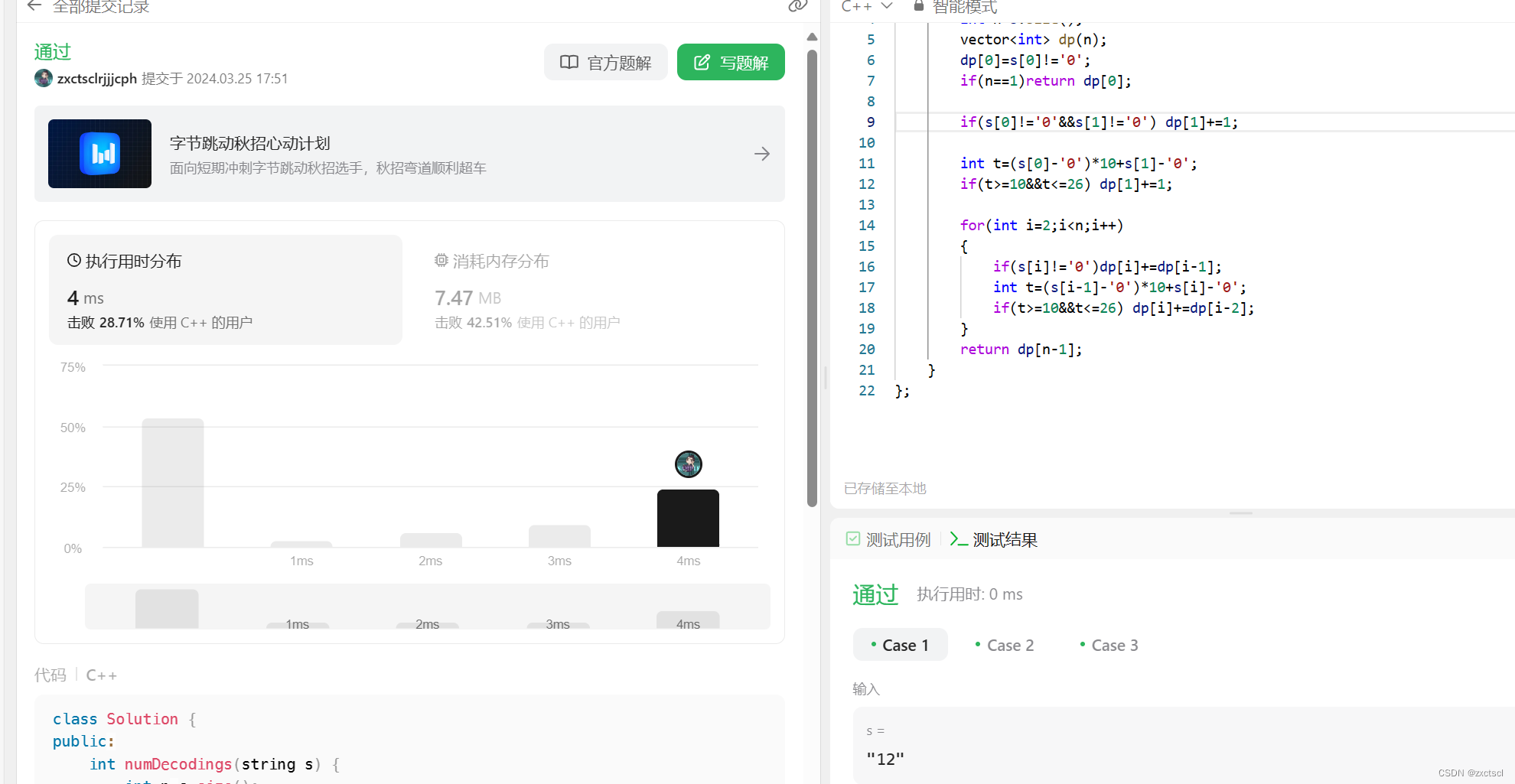
优化:处理边界以及初始化问题
多开一个虚拟位置,有什么用呢?
在旧的初始化列表中,初始化dp[1]是比较麻烦的,如果把它放在填表位置就会比较轻松。
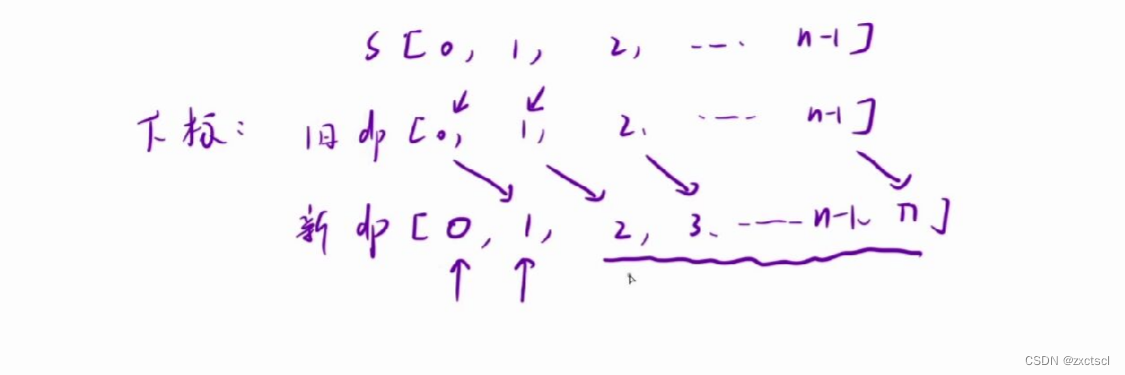
得注意:1. 保证虚拟节点位置值是正确的;2.得注意下标映射关系
当要在新的dp表里面2的结果就要用到0和1位置的值。这里dp[0]=1,要想在2位置解码成功,那么0位置必须是解码成功的。
在新的dp表里面的i统一都对应把位置往后面移动了一位,这里在写代码的时候就得减1。
1.2 代码
class Solution {
public:
int numDecodings(string s) {
int n=s.size();
vector<int> dp(n);
dp[0]=s[0]!='0';
if(n==1)return dp[0];
if(s[0]!='0'&&s[1]!='0') dp[1]+=1;
int t=(s[0]-'0')*10+s[1]-'0';
if(t>=10&&t<=26) dp[1]+=1;
for(int i=2;i<n;i++)
{
if(s[i]!='0')dp[i]+=dp[i-1];
int t=(s[i-1]-'0')*10+s[i]-'0';
if(t>=10&&t<=26) dp[i]+=dp[i-2];
}
return dp[n-1];
}
};
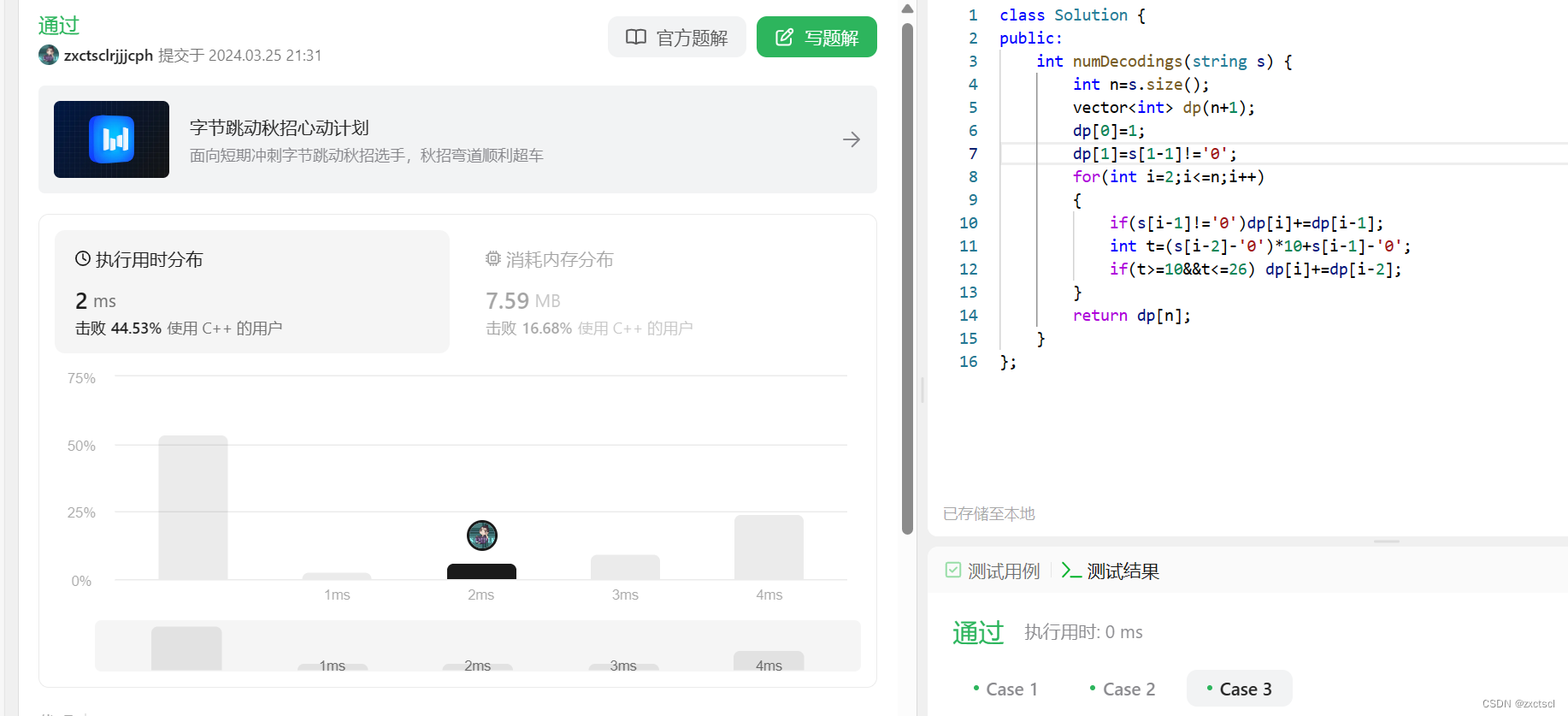
优化后:
class Solution {
public:
int numDecodings(string s) {
int n=s.size();
vector<int> dp(n+1);
dp[0]=1;
dp[1]=s[1-1]!='0';
for(int i=2;i<=n;i++)
{
if(s[i-1]!='0')dp[i]+=dp[i-1];
int t=(s[i-2]-'0')*10+s[i-1]-'0';
if(t>=10&&t<=26) dp[i]+=dp[i-2];
}
return dp[n];
}
};
2. 62.不同路径

2.1 分析
题目要求不能回退,就是不能往左和往上。
如果有3*2个表格:那么到达就有三种情况:
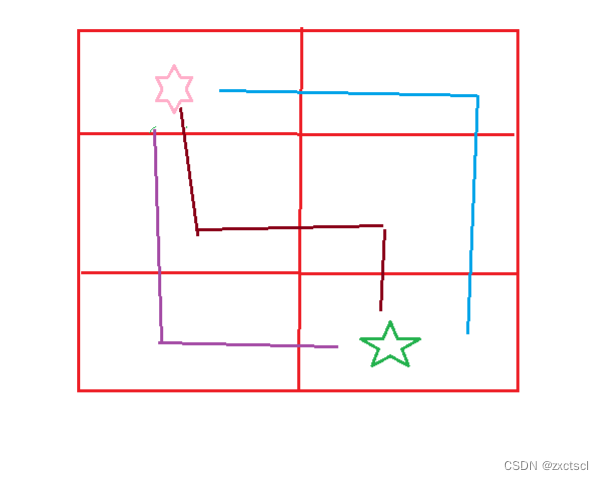
- 状态表示:以i位置为结尾,就是走到i位置有多少种方式。
- 状态转移方程:根据最近的一步划分有两种情况:到达[i][j]位置,(1)从上面一个[i-1][j]下来一步;(2)从左边[i][j-1]过来一步
状态转移方程:dp[i][j]=dp[i-1][j]+dp[i]dp[j-1]。 - 初始化,下面这些位置可能会存在越界
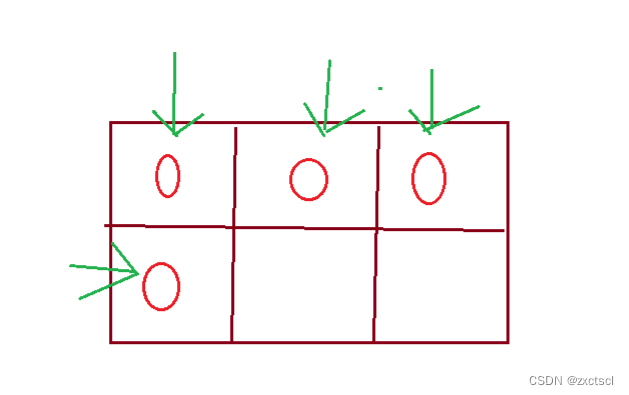
所以可以先初始化这些可能初始化的位置。还可以在外面先虚拟一些空间,让下面这些就不会越界:
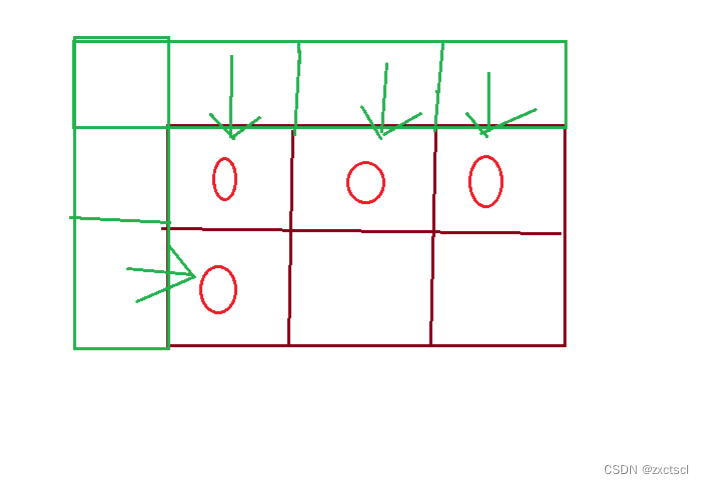
这些虚拟空间的值要保证后面填表顺序是正确的,要想填表正确,虚拟空间值设置就是:
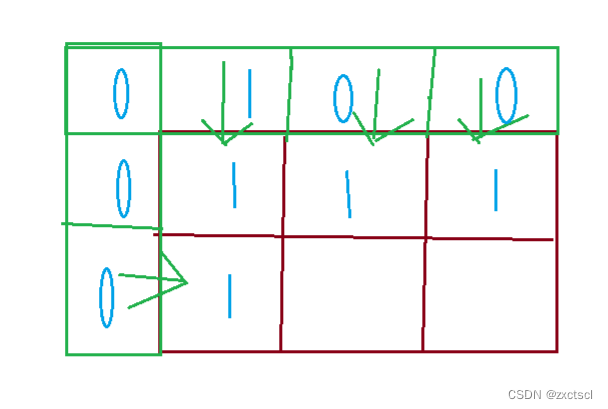
- 填表顺序:从左往右,从上往下
- 返回值:看题目要求直接返回dp[m][n]就行
2.2 代码
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[0][1] = 1;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};
3. 63.不同路径 II
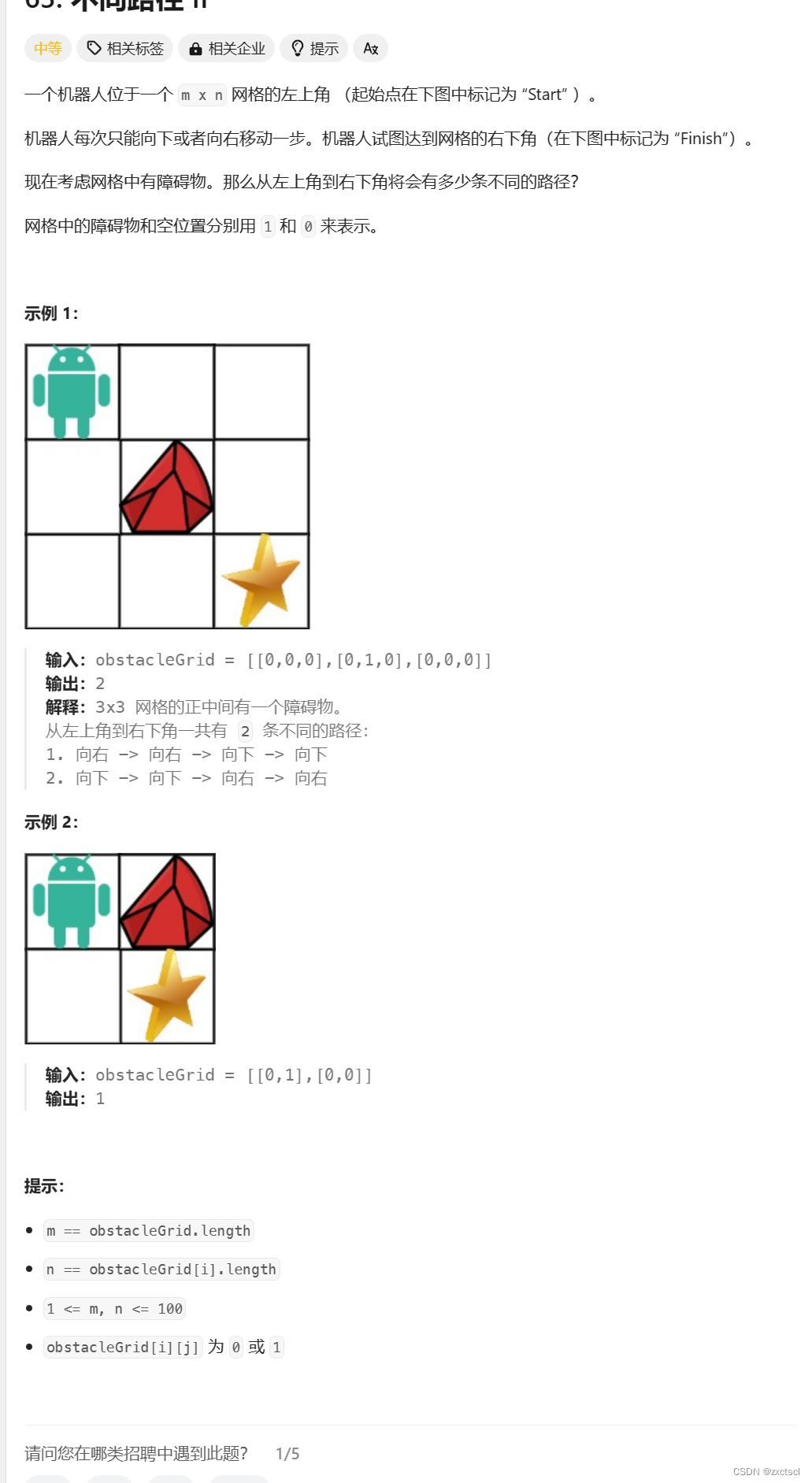
3.1 分析
题目与上面的类型是相同的,就是多了一个障碍物。
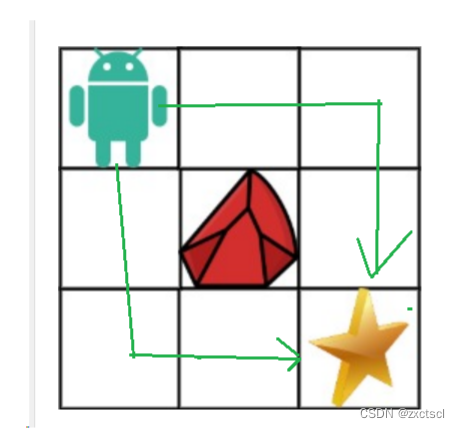
- 状态表示:以i位置为结尾,就是走到i位置有多少种方式。
- 状态转移方程:根据最近的一步划分有三种情况:到达[i][j]位置,(1)从上面一个[i-1][j]下来一步;(2)从左边[i][j-1]过来一步;(3)这个位置时障碍物那么就是0,就多加一个判断障碍物就可以了。
状态转移方程:dp[i][j]=dp[i-1][j]+dp[i]dp[j-1]。 - 初始化,下面这些位置可能会存在越界,所以就多开一组虚拟空间,得注意下标的映射。如果是障碍物位置就得对应减一。

- 填表顺序:从左往右,从上往下
- 返回值:看题目要求直接返回dp[m][n]就行
3.2 代码
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m=obstacleGrid.size(),n=obstacleGrid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[0][1] = 1;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if(obstacleGrid[i-1][j-1]==0)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};
有问题请指出,大家一起进步!!!