目录
- 1、理解多态性
- 2、怎么逆置⼀个链表
- 3、顺序表和链表的区别
- 4、树的存储结构
- 5、什么是哈夫曼树?简述哈夫曼树的构造过程。介绍哈夫曼树的特性。
- 6、哈夫曼编码的编码和解码过程
- 7、图的遍历方式
- 8、图的存储方式
- 9、最小生成树
- 10、迪杰斯特拉算法
- 11、佛洛依德算法
- 12、散列表
- 13、排序
- <font color="red">14、当键入网址后,到网页显示,其间发生了什么。
1、理解多态性
多态性就像是一只变色龙,它可以改变自己的形状和颜色来适应不同的环境。在软件工程中,多态性指的是一个对象能够表现出多种不同的行为,就像是变了个样子一样。
例如,我们可以有一个动物的类,里面有一个叫作"叫声"的方法。我们可以派生出不同的动物类,比如狗和猫。虽然它们都是动物,但是它们的叫声是不一样的。当我们调用"叫声"的方法时,根据具体是狗还是猫,它们会表现出不同的叫声。
所以,多态性就是让一个对象可以根据具体情况表现出不同的行为,就像变色龙一样。这样可以提高代码的灵活性和重用性。
Polygon p = new Polygon () ;
Rectangle r = new Rectangle () ;
p = r;
这段代码展示了多态性的概念。在这段代码中,我们首先创建了一个Polygon对象p,然后创建了一个Rectangle对象r。接下来,我们将r赋值给p,即p = r。这里发生了多态性的体现。
由于Rectangle是Polygon的子类,因此可以将Rectangle对象赋值给Polygon类型的变量。这样做的好处是可以以相同的方式处理不同类型的对象,即使用Polygon类型的变量p来调用Rectangle对象的方法。
通过这种方式,我们可以实现对不同类型对象的统一管理和操作,从而提高代码的复用性和灵活性。这就是多态性的优势所在。
2、怎么逆置⼀个链表
设置三个指针,指向链表中相邻的三个结点,依次更改每两个结点之间的链的方向,每次都进行两步操作:第一步,更改中间指针结点的next域为第一个指针,让中间的结点指向前面的结点;第二步,将这三个指针同时按照原来链表的方向向前移动
如果链表没有头结点,初始的情况需要特殊处理一下再开始重复后面的操作
3、顺序表和链表的区别
顺序表和链表是常用的两种数据结构,它们在存储和访问数据时有以下几方面的区别:
存储方式:顺序表使用一块连续的内存空间来存储数据,而链表则使用多个节点来存储数据,每个节点包含一个数据项和一个指向下一个节点的指针。
插入和删除操作:在顺序表中,插入和删除操作需要移动数据项的位置,这可能需要耗费较多的时间。而在链表中,插入和删除操作只需要修改节点的指针,所以效率较高。
访问元素:在顺序表中,可以通过下标直接访问元素,时间复杂度为O(1)。而在链表中,需要从头节点开始遍历,直到找到目标节点。所以链表的访问操作时间复杂度为O(n)。
空间占用:顺序表的空间占用是连续的,需要一块连续的内存空间,而链表的空间是分散的,每个节点可以在内存中的任意位置。
链表可以动态地分配内存空间,适用于需要频繁插入和删除操作的场景。而顺序表需要一开始就预先分配好内存,不适用于频繁插入和删除操作的场景。
根据具体的应用场景和需求,选择合适的数据结构可以提高程序的效率和性能。
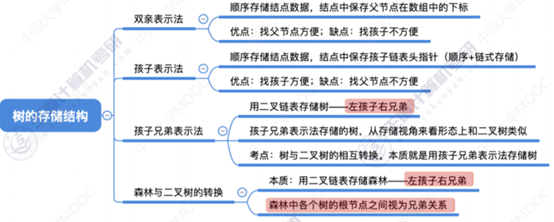
4、树的存储结构
5、什么是哈夫曼树?简述哈夫曼树的构造过程。介绍哈夫曼树的特性。
哈夫曼树是一种最优二叉树,它的带权路径长度最小,而带权路径长度就是树中所有叶结点的带权路径长度之和。
哈夫曼树的构造过程如下:
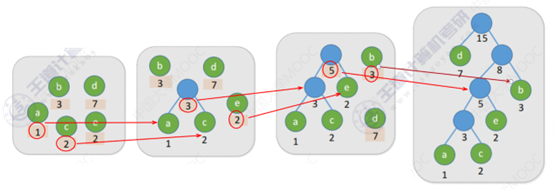
1、将原始由一个结点构成的树按照根节点权值从小到大的顺序排列
2、选择根节点权值最小的两个树,构造一个新的二叉树,将这两个树的跟结点作为新树的左右孩子,新树的根节点的权值为两个结点的权值之和
3、将新构建的树加入权值序列中,将原来的两个结点从序列中删除
4、重复前面操作,直到权值序列只剩下一个结点为止
因为这样的特性,哈夫曼树能够应用数据压缩等方面,可以大大提高解决问题的效率。比如哈夫曼编码的字符集中每个字符都作为一个叶子结点,字符的频度作为结点的权值,这样的可变长度编码可以达到数据压缩的效果,因为存储的编码的二进制个数相当于所建立的树的带权路径长度。
哈夫曼树也可以进行扩展为k叉哈夫曼树,构造过程大体和2叉哈夫曼树的构造过程相同,只不过选择结点构造新树的时候选择的是k个根节点权值最小的树,而不是2个。另外,早构造k叉二叉树之前要补充一定的虚结点,使得构造的哈夫曼树是严格k叉树,即每一个分支节点都有k个孩子。
这样的k叉哈夫曼树可以用于外部排序中的构建最佳归并树的环节中,可以大大减少访问磁盘的次数。
6、哈夫曼编码的编码和解码过程

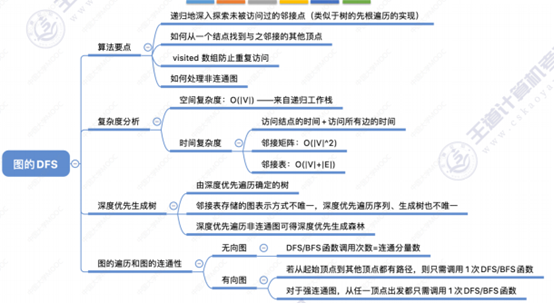
7、图的遍历方式
visited 数组防止重复访问
BFS:辅助队列、对于无向图,调用BFS函数的次数=连通分量数、空间复杂度:O(|V|)来自辅助队列
DFS:空间复杂度:O(|V|)来自递归栈
8、图的存储方式

9、最小生成树
连通图的生成树是包含图中全部顶点的一个极小连通子图
最小生成树是边权值之和最小的生成树
prim算法:从一个顶点开始构建生成树,每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。时间复杂度:O(V^2),适合边稠密
kruskal算法:每次选择一条权值最小的边,使这条边的两头连通(原本已经连通就不选),直到所有结点都连通。使⽤并查集,时间复杂度O(ElogE),适合顶点较多,边稀疏
10、迪杰斯特拉算法
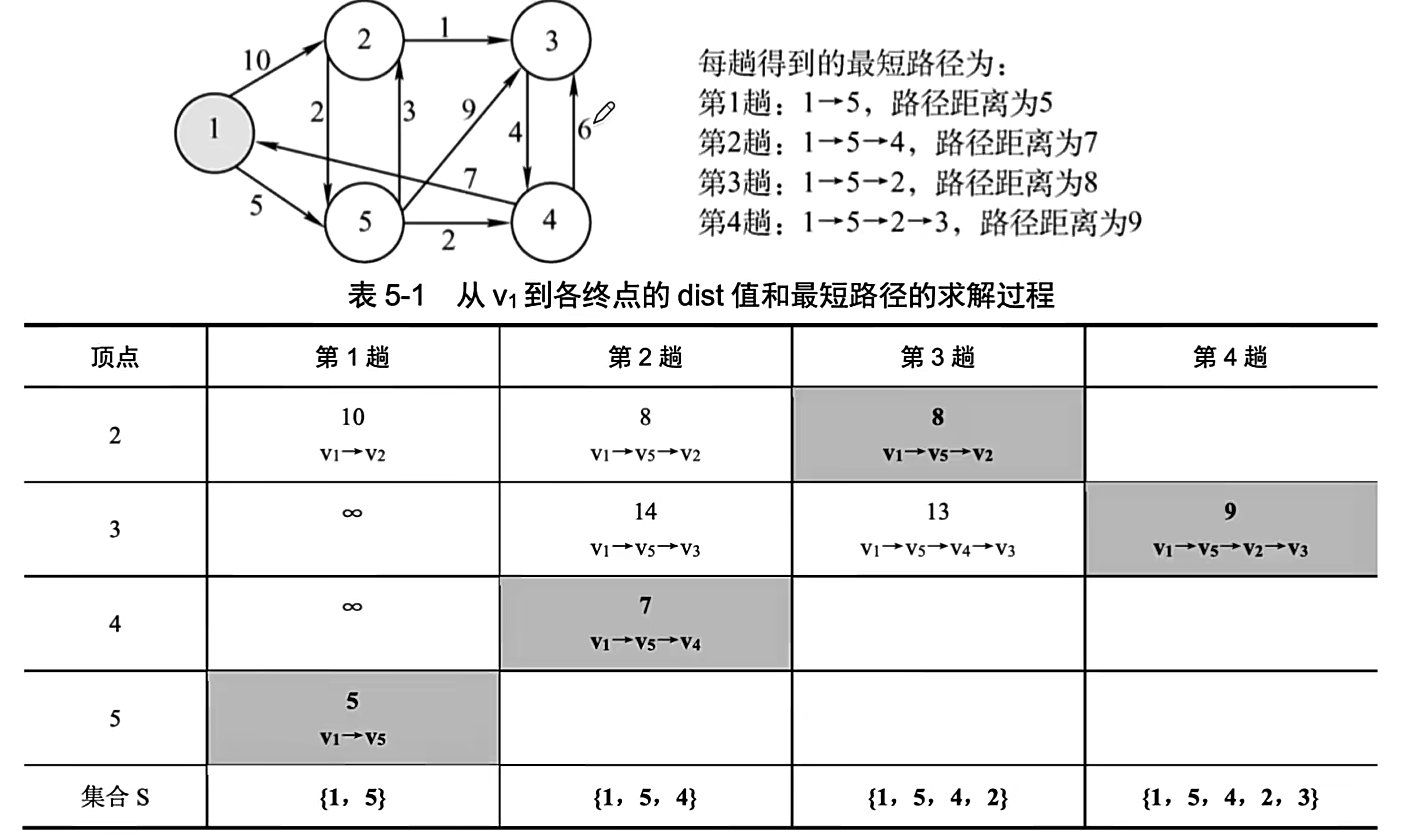
时间复杂度O(V^2)
不适合于有负权值的带权图
11、佛洛依德算法
动态规划,时间复杂度O(V^3)
不能解决带有“负权回路”的图
12、散列表

13、排序

14、当键入网址后,到网页显示,其间发生了什么。