目录

654. 最大二叉树

617. 合并二叉树

700. 二叉搜索树中的搜索

98. 验证二叉搜索树

---

 

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

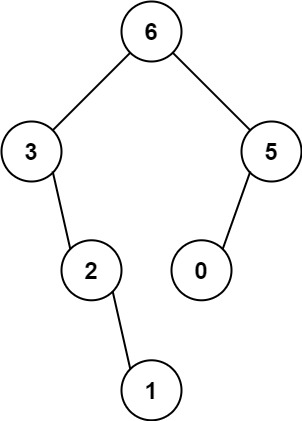
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

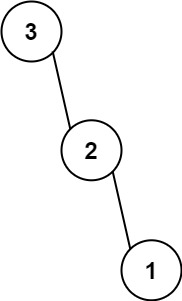
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

状态：完成

思路：先构建根节点再构建左右节点。该题使用前序遍历可以满足要求，先找出数组中此时的最大值该值则为根节点的值，然后在递归左右节点，分割数组，最后链接根节点的左右节点完成题目的要求。        

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        if(nums.length==0) return null;
        
        int index=0;
        for(int i=0;i<nums.length;i++){
            index=nums[i]>nums[index]?i:index;
        }
        TreeNode root=new TreeNode(nums[index]);
        TreeNode left=null;
        TreeNode right=null;
        if(index>0)
        left=constructMaximumBinaryTree(Arrays.copyOfRange(nums,0,index));
        if(index<nums.length-1)
        right=constructMaximumBinaryTree(Arrays.copyOfRange(nums,index+1,nums.length));
        root.left=left;
        root.right=right;
        return root;
    }
}

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• -104 <= Node.val <= 104

状态：完成

思路：前序遍历两棵树，分情况进行讨论，当两个节点都是空则返回，如果其中有一个节点不是空则返回该节点，如果两个节点都不是空的则把两个节点之和创建的新数组返回。 

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1==null&&root2==null) return null;
        TreeNode node=null;
        TreeNode left=null;
        TreeNode right=null;
        if(root1!=null&&root2!=null){
            node=new TreeNode(root1.val+root2.val);
            left =mergeTrees(root1.left,root2.left);
            right =mergeTrees(root1.right,root2.right);
        }else{
            node=root1!=null?new TreeNode(root1.val):new TreeNode(root2.val);
            if(root1!=null){
                left=mergeTrees(root1.left,null);
                right=mergeTrees(root1.right,null);
            }else if(root2!=null){
                left=mergeTrees(root2.left,null);
                right=mergeTrees(root2.right,null);
            }
        }
        node.left=left;
        node.right=right;
        return node;
    }
}

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

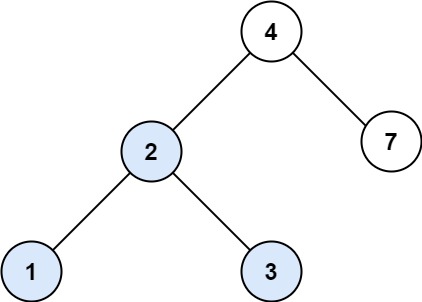
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

 状态：完成

思路：二叉搜索树的特点就是左节点小于该根节点，右节点大于该根节点则如果节点值比目标值小则搜索右子树，反之搜索左子树。

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null) return null;
        if(root.val==val) return root;
        if(root.val>val){
            TreeNode node=searchBST(root.left,val);
            return node;
        }else if(root.val<val){
            TreeNode node=searchBST(root.right,val);
            return node;
        }
        return null;
    }
}

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左

  子树

  只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

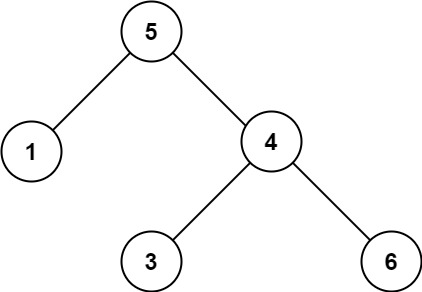
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

状态：没写出来，看思路做出来了

思路：中序遍历时结果必须是递增的才是二叉搜索树，有这个特性直接中序遍历，如果不递增则不是二叉搜索树得证。

class Solution {
    ArrayList<Integer> list=new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        mid(root);
        if(list.size()==1) return true;
        int temp=list.get(0);
        for(int i=1;i<list.size();i++){
            if(list.get(i)<=temp) return false;
            temp=list.get(i);
        }
        return true;
    }
    public void mid(TreeNode root){
        if(root==null) return;
        isValidBST(root.left);
        list.add(root.val);
        isValidBST(root.right);   
    }
}

 感想：今天学了很多二叉树的基本特性，同时力扣刷题量也突破了200+了。继续学习，持续进步。