问题描述

m*n 的二维数组 plants 记录了园林景观的植物排布情况，具有以下特性：

• 每行中，每棵植物的右侧相邻植物不矮于该植物；
  每列中，每棵植物的下侧相邻植物不矮于该植物。

题目链接：https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/description/

示例

相似题目链接（与leetcode 240题相同）: https://leetcode-cn.com/problems/search-a-2d-matrix-ii/

具体思路

  这个题目和杨氏矩阵是一样的。
  杨氏矩阵：有一个二维数组，数组的每行从左到右都是递增的，每列从上到下都是递增的，在这样的数组中查找一个数字是否存在。
例如有一个矩阵为：
1 2 3
4 5 6
7 8 9

思路一

  直接对该二维数组进行遍历，但该种方法的时间复杂度为$O(N^2)$，在此不考虑。

思路二

  我们可以找到行列的交界处，比如[0][2]，即数字3这个位置，通过观察，我们可以发现，该数字是所在行中的最大数字，所在列中的最小数字，可以用目标数target和该交界处数字进行比较，如果target大于该数，则表示比这行最大的数还要大，所以一定不在这一行，舍弃该行，向下行进行查找。 如果target小于该数，则表示target比这列最小的数还要小，所以一定不在这一列，舍弃该列，向左边行进行查找。依次类推，找到返回true，找不到返回false。

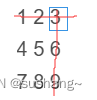
如果用[2][0]也是可以的，思路则反过来。

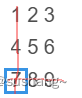
代码实现

class Solution {
public:
    bool findTargetIn2DPlants(vector<vector<int>>& plants, int target) {
		//需要考虑输入为空数组时的判断，如果是空数组的话无法对其进行访问
        if (plants.size() == 0 || plants[0].size() == 0) //plants.size()表示是有几个vector<int>（行），plants[0].size()表示第0个vector里面有多少个元素（列）
        {
            return false;
        }

        int i = 0;   //二维数组的第0行
        int j = plants[0].size() - 1;  //二维数组第0行的最后一个元素下标

        while (i < plants.size() && j >= 0)
        {
            if (target < plants[i][j])  //目标值比第0行最后一个元素小就往左边进行查找
            {
                j--;
            }
            else if (target > plants[i][j]) //目标值比第0行最后一个元素大就往下查找
            {
                i++;
            }
            else
            {
                return true;
            }
        }
        return false;
    }
};

class Solution {
public:
    bool findTargetIn2DPlants(vector<vector<int>>& plants, int target) {
        int i = plants.size() - 1, j = 0;   //最后一行的第1个元素
        while (i >= 0 && j < plants[0].size())
        {
            if (plants[i][j] > target) i--;
            else if (plants[i][j] < target) j++;
            else return true;
        }
        return false;
    }
};