一、数据准备
Logistic回归常用于解决二分类问题。
为了便于描述,我们分别从两个多元高斯分布 N₁(μ₁,Σ₁ )、N₂(μ₂,Σ₂)中生成数据 x₁ 和 x₂,这两个多元高斯分布分别表示两个类别,分别设置其标签为 y₁ 和 y₂。
PyTorch 的 torch.distributions 提供了 MultivariateNormal 构建多元高斯分布。
下面代码设置两组不同的均值向量和协方差矩阵,μ₁(mul)和 μ₂(mul)是二维均值向量,Σ₁(sigmal)和Σ₂(sigma2)是2*2的协方差矩阵。

前面定义的均值向量和协方差矩阵作为差数传入 MultivariateNormal,就实例化了两个多元高斯分布 m₁和 m₂。
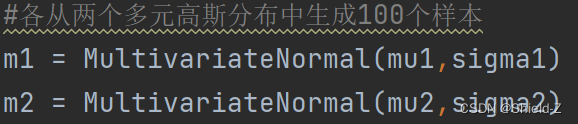
调用 m₁和 m₂ 的sample方法分别生成100个样本。
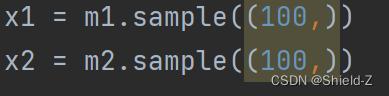
设置样本对应的标签 y,分别用 0 和 1 表示不同高斯分布的数据,也就是正样本和负样本。
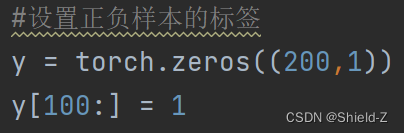
使用 cat 函数将 x₁(m1)和 x₂(m2)组合在一起。

打乱样本和标签的顺序,将数据重新随机排列,这是十分重要的步骤,否则算法的每次迭代只会学习到同一个类别的信息,容易造成模型过拟合。
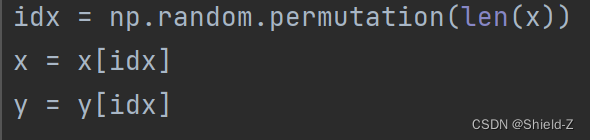
将生成的样本用 plt.scatter 绘制出来。

绘制结果如图:
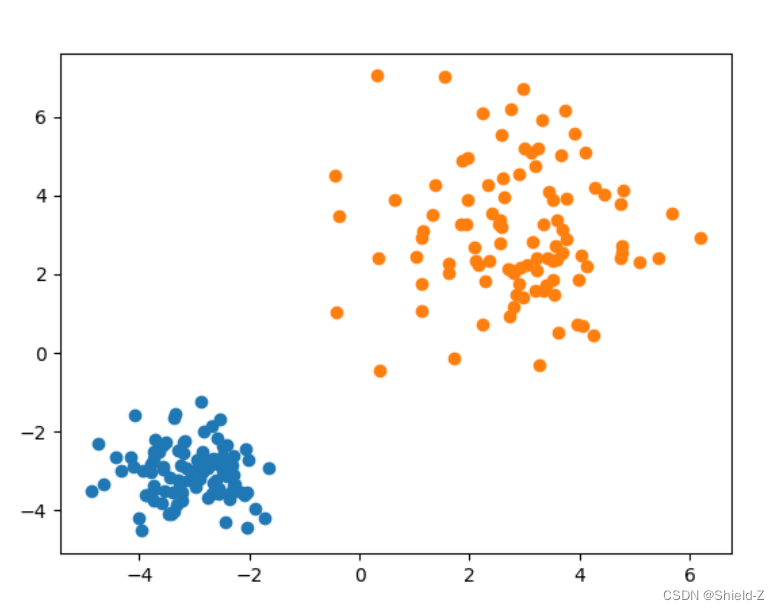
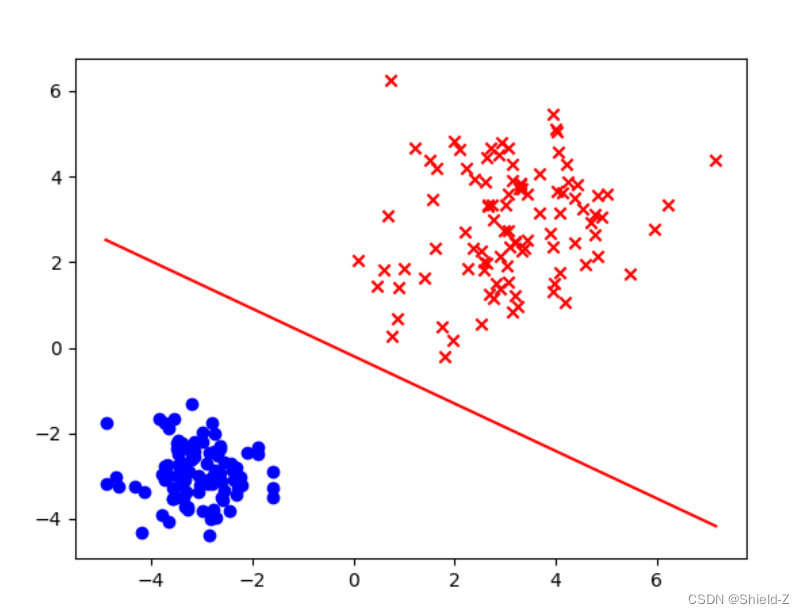
可以明显的看出多元高斯分布生成的样本聚成了两个簇,并且簇的中心分别处于不同的位置(多元高斯分布的均值向量决定了其位置)。
右上角簇的样本分布比较稀疏,而左下角簇的样本分布紧凑(多元高斯分布的协方差矩阵决定了分布形状)。
【可调整
mu1 = -3 * torch.ones(2)
mu2 = 3 * torch.ones(2)
的参数,观察变化!
】
二、线性方程
Logistic回归用输入变量x的线性函数表示样本为正类的对数概率。nn.Linear 实现了 y = xAᵀ + b,我们可以直接调用它来实现Logistic回归的线性部分。
定义线性模型的输入维度D_in 和输出维度 D_out,因为前面定义的多元高斯分布 m₁(m1)和 m₂(m2)产生的变量是二维的,所以线性模型的输入维度应该定义为D_in = 2 ;而Logistic回归是二分类模型,预测的是变量为正类的概率,所以输出的维度应该为D_in = 1。
![]()
实例化了nn.Linear,将线性模型应用到数据 x 上,得到计算结果output。

Linear的初始参数是随机设置的,可以调用Linear.weight 和 Linear.bias 获取线性模型的参数。
输出输入的变量x,模型参数weight和bias,以及计算结果output的维度。

定义线性模型my_linear,将my_linear的计算结果和PyTorch的计算结果output进行比较,可以发现他们是一致的。

输出:

三、激活函数
前面介绍了nn.Linear可用于实现线性模型,除此之外,torch.nn还提供了机器学习中常用的激活函数。当Logistic回归用于二分类问题时,使用sigmoid函数将线性模型的计算结果映射到0和1之间,得到的计算结果作为样本为正类的置信概率。nn.Sigmoid提供了sigmoid函数的计算,在使用时,将Sigmoid类实例化,再将需要计算的变量作为参数传递给实例化的对象。

输出:

【def my_sigmoid(x):
x = 1 / (1 + torch.exp(-x))
return x手动实现sigmoid函数;
print(torch.sum(sigmoid(output) - sigmoid_(output)))通过PyTorch验证我们的实现结果,其结果一致】
四、损失函数
1、
Logistic回归使用交叉熵作为损失函数
PyTorch的torch.nn提供了许多标准的损失函数,我们可以直接使用 nn.BCELoss 计算二值交叉熵损失。
调用BCELoss来计算我们实现Logistic回归模型的输出结果sigmoid(output)和数据的标签y。
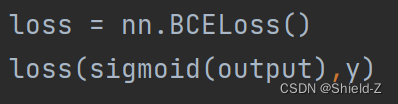
自定义二值交叉熵函数

将my_loss 和PyTorch的BCELoss进行比较,发现其结果一致。

2、
前面的代码中,我们使用了torch.nn包中的线性模型nn.Linear、激活函数nn.Softmax、损失函数nn.BCELoss,他们都继承自nn.Module类。
而在PyTorch中,我们通过继承nn.Module来构建我们自己的模型。
下面用nn.Module来实现Logistic回归。
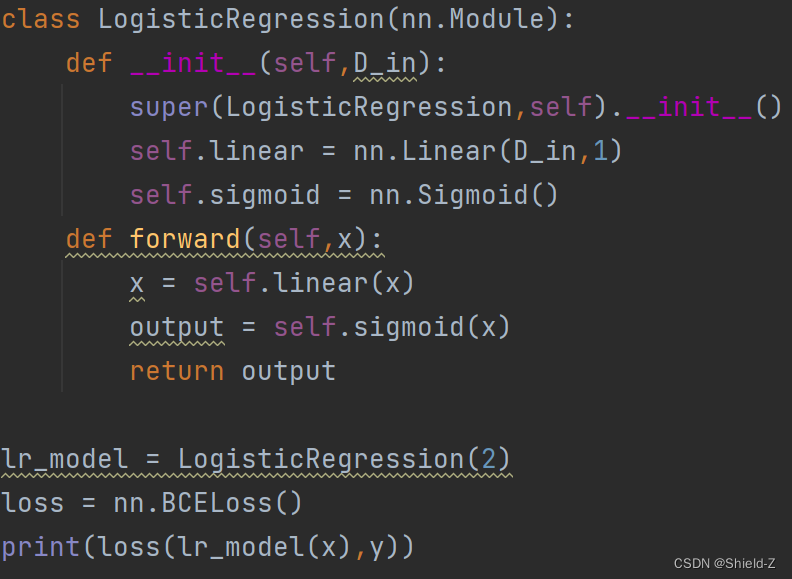
输出:

3、
当通过继承nn.Module实现自己的模型时,forward方法是必须被子类覆写的,
在forward内部应当定义每次调用模型时执行的计算。
从代码中可以看出,nn.Module类的主要作用就是接收Tensor然后计算并返回结果。
在一个Module中,还可以嵌套其他的Module,被嵌套的Module的属性就可以被自动获取,比如可以调用nn.Module.parameters方法获取Module所有保留的参数,调用nn.Module.to方法将模型的参数放置到GPU上等。
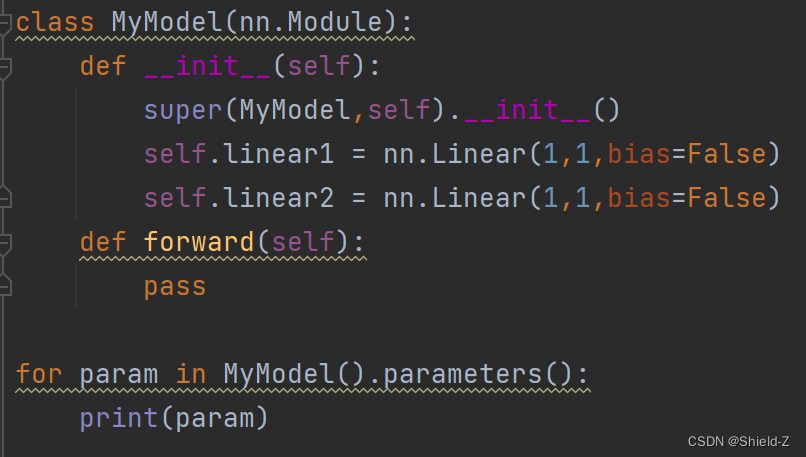
输出:
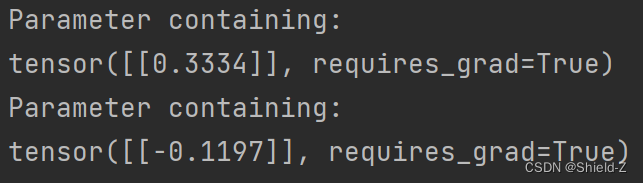
五、优化算法
Logistic回归通常采用梯度下降法优化目标函数。
PyTorch的torch.optim包实现了大多数常用的优化算法,使用起来非常简单。
首先构建一个优化器,在构建时,需要将学习的参数传入,然后传入优化器需要的参数,比如学习率。

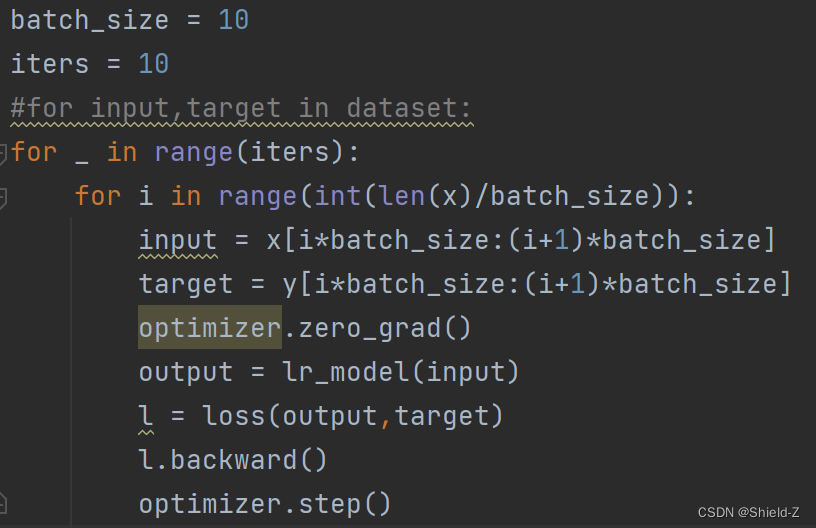
构建完优化器,就可以迭代地对模型进行训练,
两个步骤:
(1)调用损失函数的backward方法计算模型的梯度
(1)调用优化器的step方法更新模型的参数。
需要注意:应当提前调用优化器的zero_grad方法清空参数的梯度。
六、模型可视化
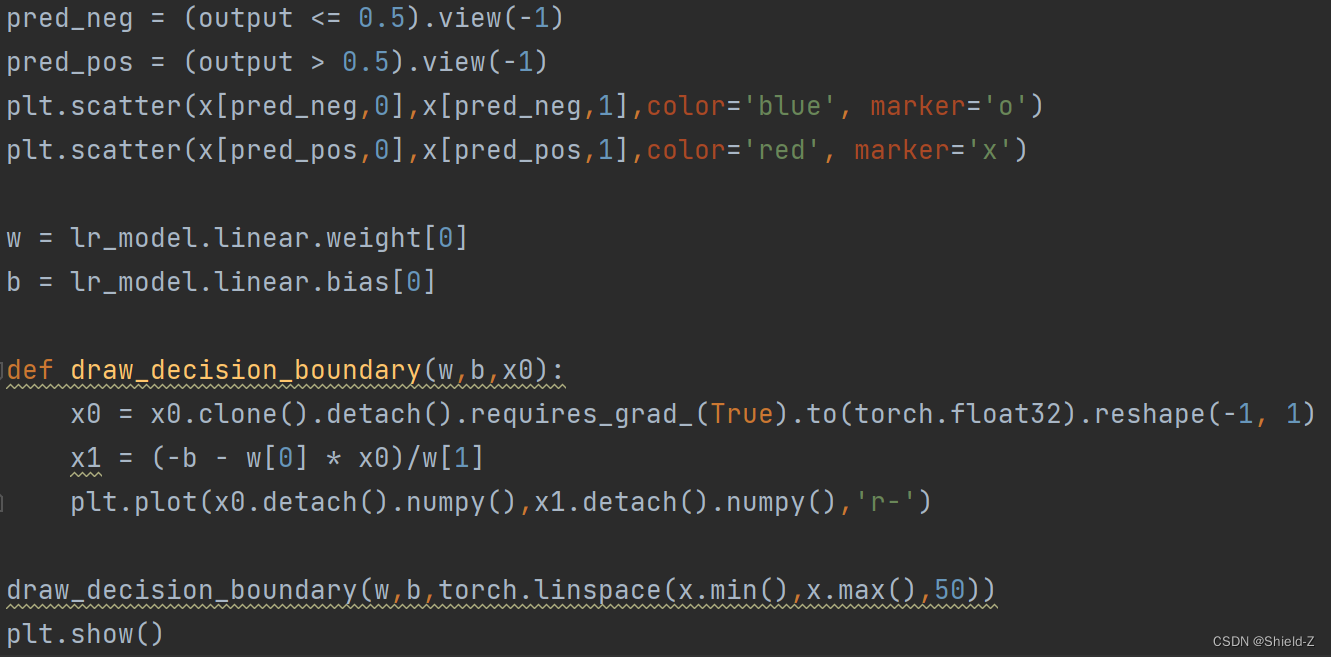
Logistic回归模型的判决边界在高维空间是一个超平面,而我们的数据集是二维的,所以判决边界只是平面内的一条直线,在线的一侧被预测为正类,另一侧被预测为负类。下面我们实现draw_decision_boundary函数。
它接收线性模型的参数w和b,以及数据集x。
绘制判决边界的方法十分简单。
如![]() ,只需要计算一些数据在线性模型的映射值,然后调用plt.plot绘制线条即可。如下图:
,只需要计算一些数据在线性模型的映射值,然后调用plt.plot绘制线条即可。如下图:
--------------------------------------------------------------------------------------------------------------
七、回归VS分类
在之前的回归任务中,我们是预测分值是多少;
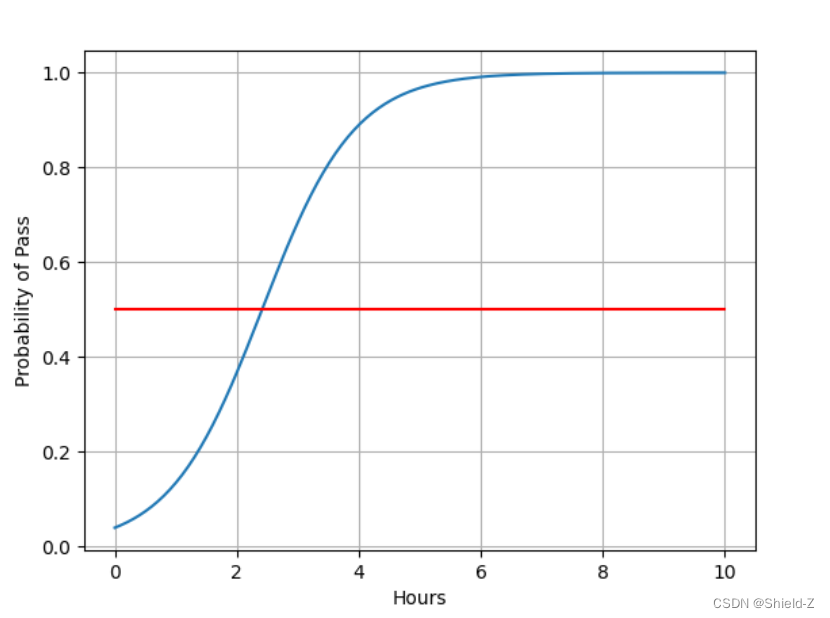
在分类任务中就可以变成根据学习时间判断是否能通过考试,即结果分为两类:fail、pass。
我们的任务就是计算不同时间 x 分别是 fail、pass 的概率。(二分类问题其实只需要计算一个概率; 另一个概况就是1-算的概率)
如果预测pass概率为0.6,fail概率就是0.4,那么判断为pass。

1、sigmoid函数
σ(x)= 1 / 1+e⁻ˣ
sigmoid函数在x无限趋近于正无穷、 负无穷时,y无线趋近于1、0;
可以看到当x非常大或者非常小的时候,函数梯度变化就非常小了。这 种函数称为饱和函数
八、逻辑回归
1、逻辑回归模型
只是在线性回归之后加了一个sigmoid激活函数!将值映 射在【0,1】之间。
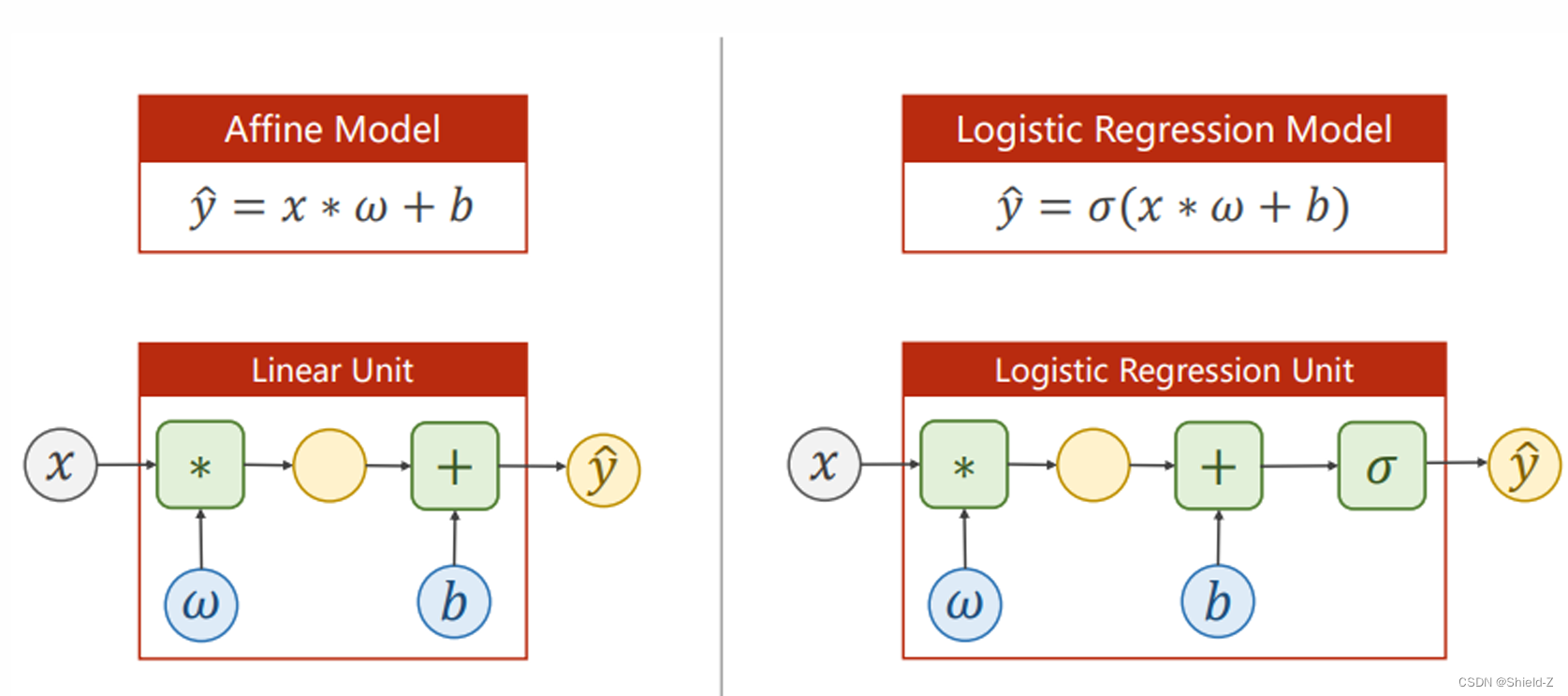
在线性回归中,我们假设随机变量𝑥1,⋯,𝑥𝑛与𝑦之间的关系是线性的。
但在实际中,我们通常会遇到非线性关系。这个时候,我们可以使用一个非线性变化g(·),使得线性回归模型 𝑓(⋅) 实际上对g(y)而非y进行拟合,即:
y = g⁻¹(f(x))
其中 f(·)仍为:
f(x)= wᵀx + b
因此这样的回归模型称为广义线性回归模型。
广义线性回归模型使用非常广泛。例如在二元分类任务中,我们的目标是拟合这样一 个分离超平面𝑓(𝒙)=𝒘ᵀ𝒙+𝑏,使得目标分类𝑦可表示为以下阶跃函数:
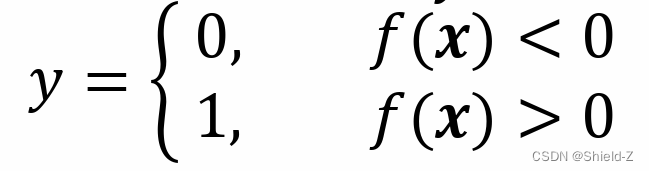
但是在分类问题中,由于𝑦取离散值,这个阶跃判别函数是不可导的。
不可导的性质使得许多数学方法不能使用。我们考虑 通常可以使用一个函数σ(·)来近似这个离散的阶跃函数,通常可以使用 logistic(Sigmoid函数)
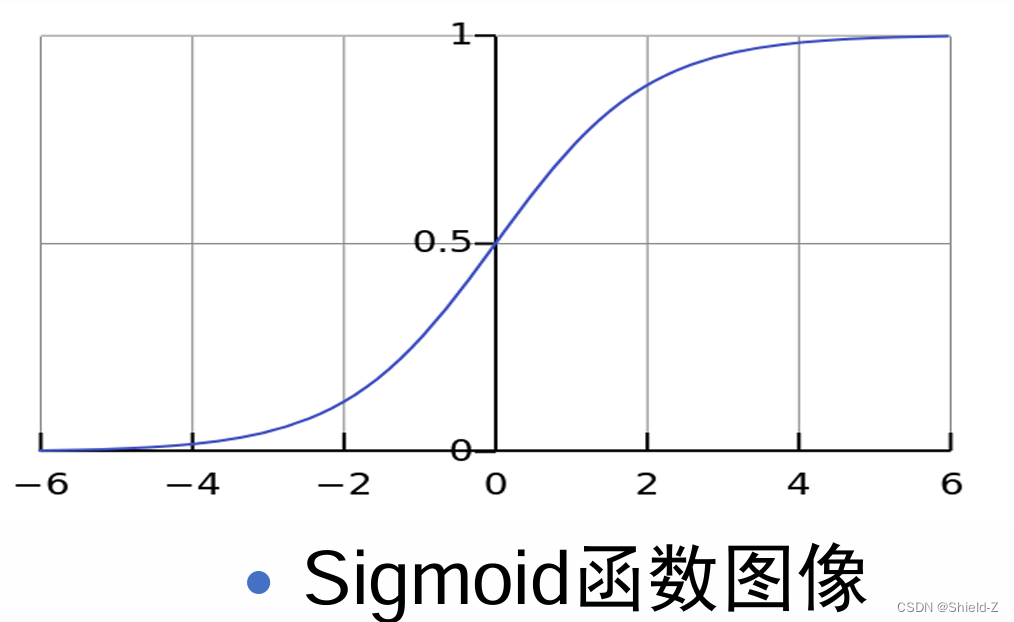
2、损失函数
MSE loss:计算 数值之间的差异
BCE loss:计算 分布之间的差异

3、Logistic回归代码实现
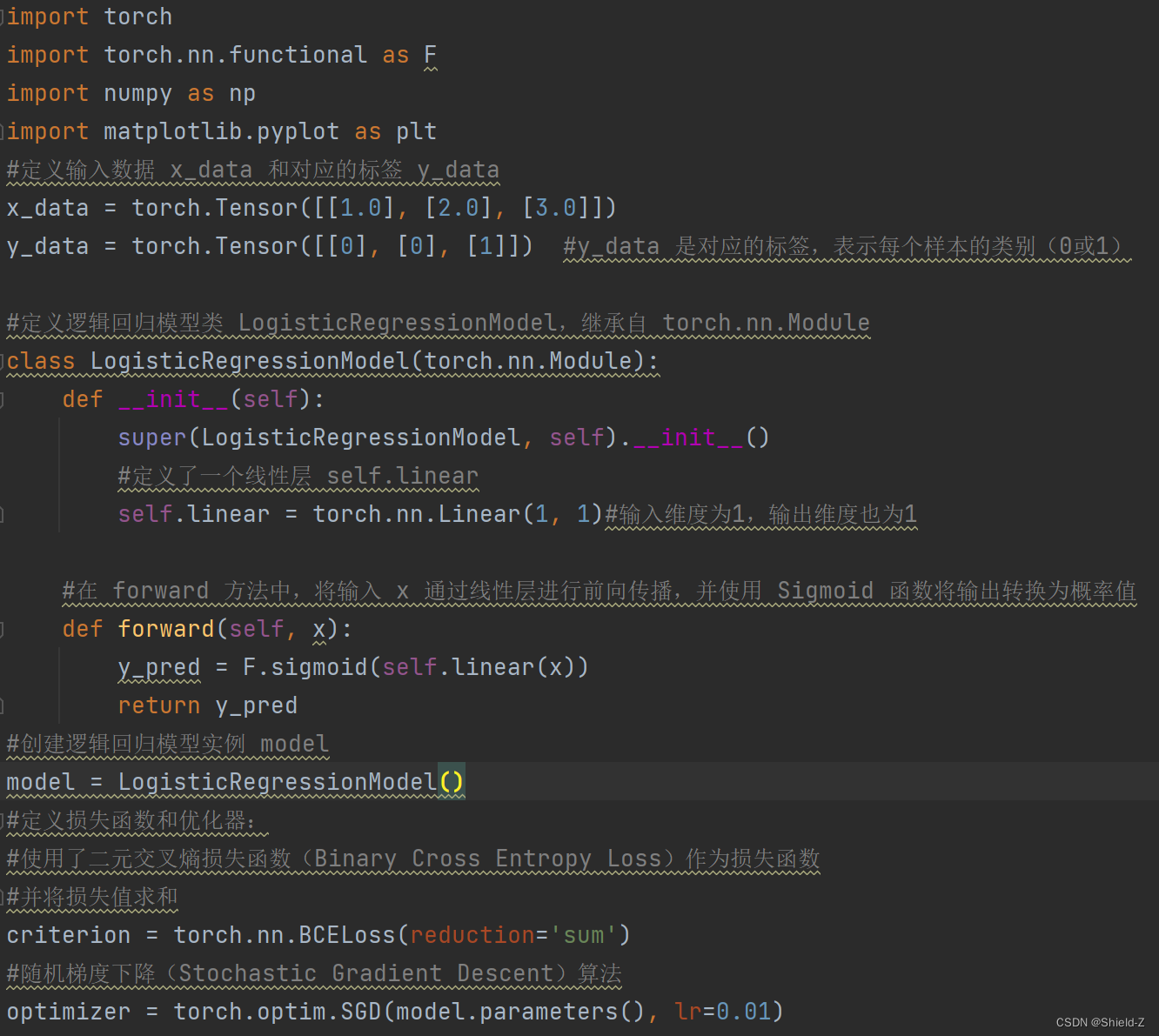
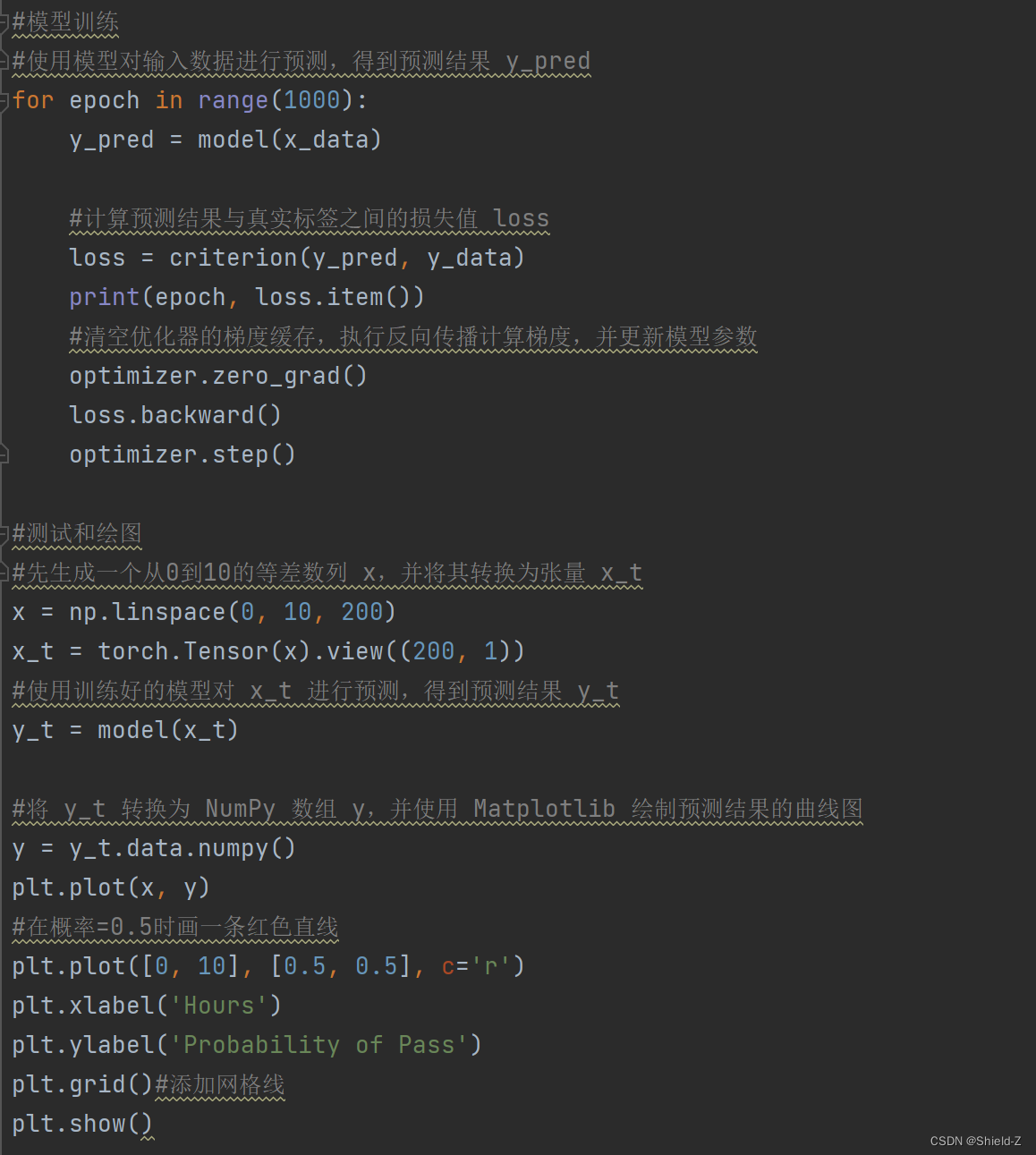
训练结果为: