目录

经验模态分解（EMD）

希尔伯特谱分析（HSA）

定义

连续时信号的Hilbert变换定义

离散时信号的Hilbert变换定义

解析信号定义：

解析信号的傅里叶变换

解析信号的重要意义

解析信号的属性

希尔伯特--黄变换（HHT）

HHT结果作用

---

《The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis》

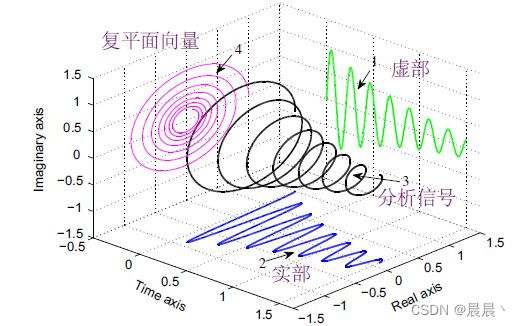
希尔伯特-黄变换（Hilbert-Huang Transform, HHT）是一种用于分析非线性和非平稳时间序列的方法。这种方法是由NASA的黄锷华教授在1998年提出的。HHT由两个主要步骤组成：经验模态分解（Empirical Mode Decomposition, EMD）和希尔伯特谱分析（Hilbert Spectral Analysis, HSA）。

经验模态分解（EMD）

EMD的目的是将一个复杂的数据集分解成一系列称为本征模态函数（Intrinsic Mode Functions, IMFs）的简单波形。IMF是满足两个条件的函数：在整个数据集中，极值点的数量和零点的数量必须相等或者相差至多一；在任何点，局部平均值（由局部极大值和极小值形成的包络线的平均值）必须为零。

EMD的分解过程是递归进行的，从原始数据开始，通过局部极值识别、包络线创建和平均值去除，逐步提取出IMFs。每一步提取出的IMF都是数据中最快变化的部分，提取后，从数据中去除这一部分，继续对剩余的数据进行同样的处理，直到剩余的数据不能再分解为止。

希尔伯特谱分析（HSA）

提取出IMFs后，接下来使用希尔伯特变换（Hilbert Transform）对每个IMF进行分析，得到每个IMF随时间变化的瞬时频率。希尔伯特变换是一种计算解析信号的方法，解析信号是一种复数表示的信号，它的实部是原信号，虚部是原信号的希尔伯特变换。通过解析信号可以计算瞬时频率和瞬时振幅，进而获得原信号的频率随时间变化的信息。

定义

希尔伯特变换定义为原信号 x(t) 与函数 1/(πt) 的卷积，表达式为：

连续时信号的Hilbert变换定义

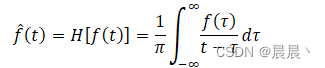
反变换:

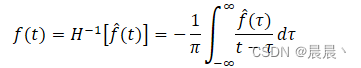
即：

离散时信号的Hilbert变换定义

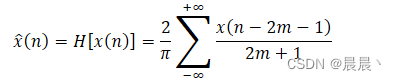
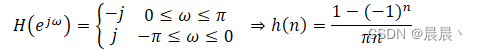
解析信号定义：

解析信号是一种复数信号，其目的在于提供一种方式，通过将实值信号转换为复数形式，从而能失从中直接提取出信号的瞬时幅度和瞬时频率等信息。解析信号的构造基于原信号和其希尔伯特变换的结合。希尔伯特变换是一种线性操作，用于产生与原信号 f(t) 相对应的信号 f'(t)，其中 f'(t) 是 f(t) 的90度相位移动版本。然后，原信号和它的希尔伯特变换结合成解析信号 z(t)，形式如下：

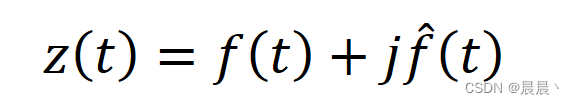
解析信号的傅里叶变换

解析信号的重要意义

特变是对于IMF（本征信号--EMD），幅度变化的足够慢，Bedrosian 定理适用，解析信号直接继承相同的幅度函数。

解析信号的属性

1. 瞬时幅度与瞬时相位：解析信号的模表示瞬时幅度（或包络），而其角度（或相位）表示瞬时相位。这些可以直接从复数信号中计算得出，无需进行复杂的时频分析。

2. 瞬时频率：瞬时频率可以通过计算解析信号相位的时间导数获得。这是分析非平稳信号中频率随时间变化的一种非常有用的方法。

希尔伯特变换最突出的用途是从纯实信号构造分析信号。

 

自己的一些理解：

解析信号是一种没有负频率分量的复值函数，解析信号的实部和虚部是通过希尔伯特变换相互联系的实值函数。

实值函数的解析表示是一个解析信号，由原函数及其希尔伯特变换组成。（基本思想是，实值函数的傅里叶变换(或频谱)的负频率分量是多余的，因为这种频谱具有Hermit对称性）

只要被操纵的函数没有负的频率分量，即解析信号。

解析表示是相量概念的推广：当相量被限制为时不变的幅值、相位和频率时，解析信号允许时变参数。

希尔伯特求信号的瞬时频率：

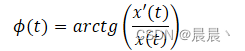
希尔伯特变换只能近似地应用于窄带信号，对任意给定的t时刻，通过希尔伯特变换运算得到的结果只能存在一个频率，即只能处理任何时刻为单一频率的信号。对于非平稳的信号序列，希尔伯特变换得到的结果很大程度上失去了原有的物理意义。

当采用Hilbert变换处理非平稳信号瞬时频率时，出现了负频率。-->解决方法：黄锷（EMD）

EMD将非平稳信号分解为多个平稳信号的叠加。

分开的每个分量称为IMF（内涵模态分量Intrinsic Mode Function）

希尔伯特变换适用与窄带信号，窄带的定义：

在物理上，如果瞬时频率有意义，那么函数必须是对称的，局部均值为零，并且具有相同的过零点和极值点数目。

希尔伯特--黄变换（HHT）

把经过EMD分解出的IMF分量再经过Hiberti变换，最终得到信号瞬时频率和瞬时幅值的方法叫做希尔伯特黄变换。

HHT结果作用

1、HHT结果反映的是信号的时频特性，即信号的频域特征随时间变化的规律。

2、HHT可以对局部特征进行反映，这点主要得益于EMD的作用。EMD可以自适应地进行时频局部化分析，有效提取原信号的特征信息。

3、“分解”往往可以对应着“重构”，从HHT结果中选择出满足要求的特征分量并重组信号，有利于将关注的特征从复杂的混合信号中分离出来。

• 用来构建解析信号，使信号频谱仅含有正频率成分，从而降低信号的抽样率；
• 可以用来表示带通信号，从而为无线电通信中的信号调制提供了一种方法；
• 与其他变换及分解结合在一起，进行非平稳信号的频谱分析。