摘要
PKINet是面向遥感旋转框的主干,网络包含了CAA、PKI等模块,给我们改进卷积结构的模型带来了很多启发。本文使用PKINet的Block替换YoloV8的Block,实现涨点。改进方法是我独创首发,给写论文没有思路的同学提供改进思路,欢迎大家订阅!
论文:《Poly Kernel Inception Network在遥感检测中的应用》
https://export.arxiv.org/pdf/2403.06258
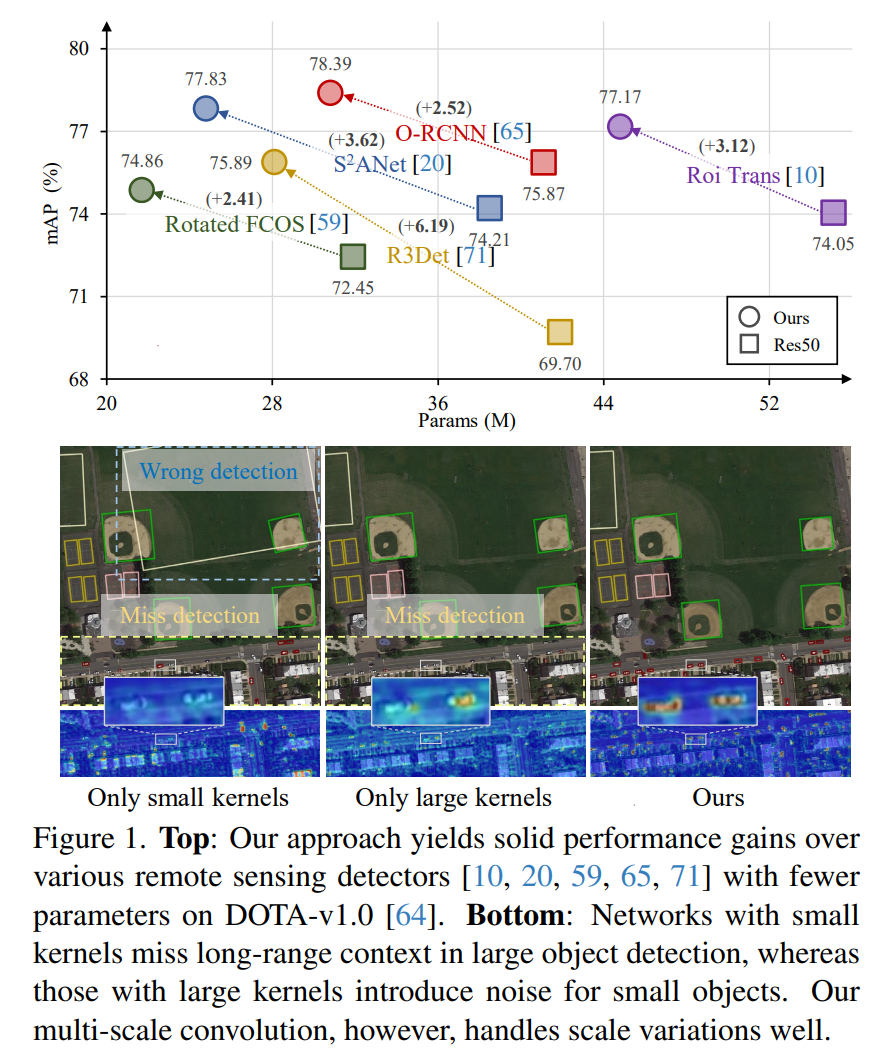
遥感图像(RSI)中的目标检测经常面临一些日益严重的挑战,包括目标尺度的巨大变化和多样的上下文环境。先前的方法试图通过扩大骨干网络的空间感受野来解决这些挑战,要么通过大核卷积,要么通过空洞卷积。然而,前者通常会引入大量的背景噪声,而后者则可能生成过于稀疏的特征表示。在本文中,我们引入了Poly Kernel Inception Network(PKINet)来处理上述挑战。PKINet采用无空洞的多尺度卷积核来提取不同尺度的目标特征并捕获局部上下文。此外,我们还并行引入了一个Context Anchor Attention(CAA)模块来捕获长距离上下文信息。这两个组件共同作用,提高了PKINet在四个具有挑战性的遥感检测基准上的性能,即DOTA-v1.0、DOTA-v1.5、HRSC2016和DIOR-R。
1、简介
遥感图像(RSI)中的目标检测