最小二乘法,又称最小平方法,起源于十八世纪的大航海探索时期,发展于天文领域和航海领域。其历史可以追溯到法国科学家马里·勒让德于1805年首次提出这一概念,而1809年,高斯在他的著作《天体运动论》中也提出了最小二乘法,并发表了应用该方法计算谷神星轨道的结果。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星,这进一步验证了最小二乘法的有效性。此后,高斯在1829年证明了最小二乘法的优化效果强于其他方法,这被称为高斯-马尔可夫定理。
在发展过程中,最小二乘法逐渐形成了两类基本算法:传统的一次完成算法和最小二乘递推算法。前者具体方法视所用输入信号而定,常见的输入信号有随机序列、伪随机序列等。后者更易于在微机上实现,适用于参数在线辨识。
然而,最小二乘法在应用中并非完美无缺。由于它基于最小化误差平方和的原理,因此在处理含有随机特性的系统时,可能会引进偏差,且易受到噪声的干扰,导致精度不佳。只有在方程中只拥有白噪声误差时,其算法精度才能达到理想状态。
尽管存在这些挑战,但最小二乘法仍被广泛应用于误差估计、曲线拟合、参数辨识、预测、预报等领域。此外,随着技术的发展,最小二乘法也在不断地改进和优化,以适应更广泛和复杂的应用场景。
利用最小二乘法拟合曲线的一般步骤是:
-
将实验数据显示出来,分析曲线的形式;
-
确定拟合曲线的形式。对于本文来说,曲线形式是直线,y=a+bx;
-
建立法方程组并对其进行求解;
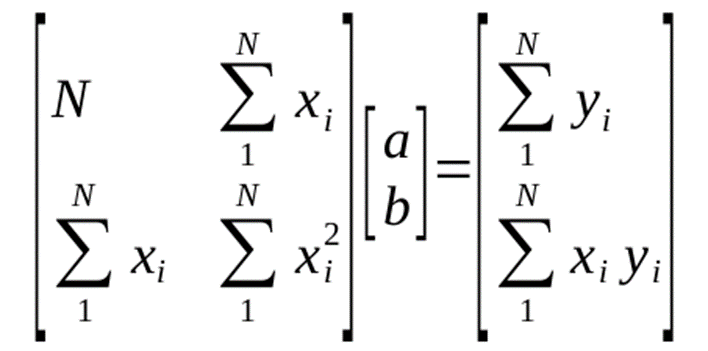
#include <iostream>#include <gp_Lin2d.hxx>#include <gp_Pnt2d.hxx>#include <TColgp_Array1OfPnt2d.hxx>#include <math_Vector.hxx>#include <math_SVD.hxx>#include <math_Gauss.hxx>#include <math_GaussLeastSquare.hxx>#include <OSD_Chronometer.hxx>void fitLine(const TColgp_Array1OfPnt2d& thePoints,const std::string& theFileName,gp_Lin2d& theLine){math_Vector aB(1, 2, 0.0);math_Vector aX(1, 2, 0.0);math_Matrix aM(1, 2, 1, 2);Standard_Real aSxi = 0.0;Standard_Real aSyi = 0.0;Standard_Real aSxx = 0.0;Standard_Real aSxy = 0.0;std::ofstream aDrawFile(theFileName);for (Standard_Integer i = thePoints.Lower(); i <= thePoints.Upper(); ++i){const gp_Pnt2d& aPoint = thePoints.Value(i);aSxi += aPoint.X();aSyi += aPoint.Y();aSxx += aPoint.X() * aPoint.X();aSxy += aPoint.X() * aPoint.Y();aDrawFile << "vpoint p" << i << " " <<aPoint.X() << " " << aPoint.Y() << " 0" << std::endl;}aM(1, 1) = thePoints.Size();aM(1, 2) = aSxi;aM(2, 1) = aSxi;aM(2, 2) = aSxx;aB(1) = aSyi;aB(2) = aSxy;OSD_Chronometer aChronometer;aChronometer.Start();math_Gauss aSolver(aM);//math_GaussLeastSquare aSolver(aM);//math_SVD aSolver(aM);aSolver.Solve(aB, aX);if (aSolver.IsDone()){Standard_Real aA = aX(1);Standard_Real aB = aX(2);gp_Pnt2d aP1(0.0, aA);gp_Pnt2d aP2(-aA/aB, 0.0);theLine.SetLocation(aP1);theLine.SetDirection(gp_Vec2d(aP1, aP2).XY());aDrawFile << "vaxis l "<< aP1.X() << " " << aP1.Y() << " 0 "<< aP2.X() << " " << aP2.Y() << " 0 " << std::endl;std::cout << "===================" << std::endl;aX.Dump(std::cout);}aChronometer.Stop();aChronometer.Show();}int main(){gp_Lin2d aLine;// Test data 1TColgp_Array1OfPnt2d aPoints1(1, 6);aPoints1.SetValue(1, gp_Pnt2d(36.9, 181.0));aPoints1.SetValue(2, gp_Pnt2d(46.7, 197.0));aPoints1.SetValue(3, gp_Pnt2d(63.7, 235.0));aPoints1.SetValue(4, gp_Pnt2d(77.8, 270.0));aPoints1.SetValue(5, gp_Pnt2d(84.0, 283.0));aPoints1.SetValue(6, gp_Pnt2d(87.5, 292.0));fitLine(aPoints1, "fit1.tcl", aLine);// Test data 2TColgp_Array1OfPnt2d aPoints2(0, 7);aPoints2.SetValue(0, gp_Pnt2d(0.0, 27.0));aPoints2.SetValue(1, gp_Pnt2d(1.0, 26.8));aPoints2.SetValue(2, gp_Pnt2d(2.0, 26.5));aPoints2.SetValue(3, gp_Pnt2d(3.0, 26.3));aPoints2.SetValue(4, gp_Pnt2d(4.0, 26.1));aPoints2.SetValue(5, gp_Pnt2d(5.0, 25.7));aPoints2.SetValue(6, gp_Pnt2d(6.0, 25.3));aPoints2.SetValue(7, gp_Pnt2d(7.0, 24.8));fitLine(aPoints2, "fit2.tcl", aLine);return 0;}