DFS(depth first search) 深度优先遍历
从图中一个未访问的顶点V开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路走到底…不断递归重复这个过程,直到所有的顶点都遍历完成。前序遍历,还是中序遍历,亦或是后序遍历,都属于深度优先遍历。
树是图的一种特例(连通无环的图就是树),接下来我们来看看树用深度优先遍历该怎么遍历。
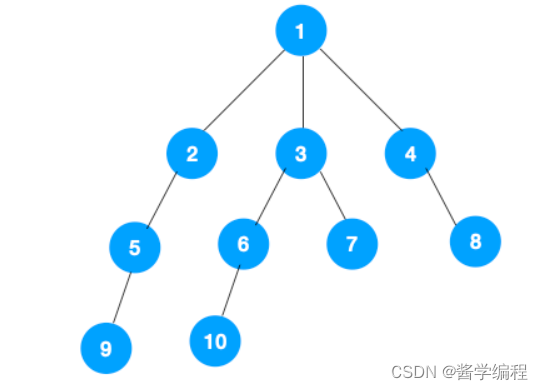
1、我们从根节点 1 开始遍历,它相邻的节点有 2,3,4,先遍历节点 2,再遍历 2 的子节点 5,然后再遍历 5 的子节点 9。
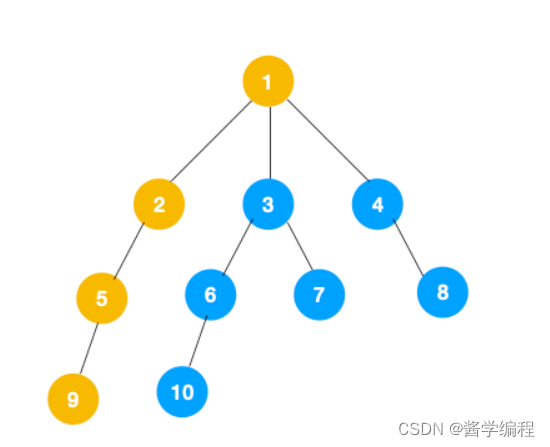
2、上图中一条路已经走到底了(9是叶子节点,再无可遍历的节点),此时就从 9 回退到上一个节点 5,看下节点 5 是否还有除 9 以外的节点,没有继续回退到 2,2 也没有除 5 以外的节点,回退到 1,1 有除 2 以外的节点 3,所以从节点 3 开始进行深度优先遍历,如下
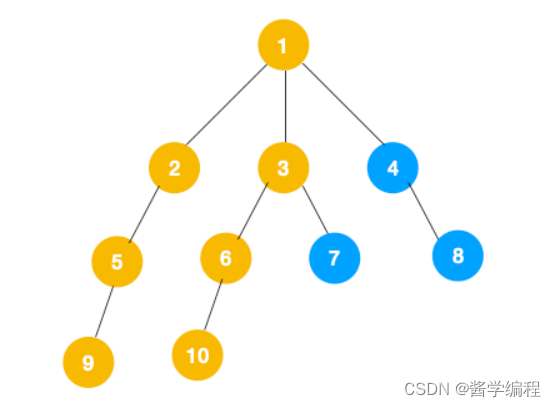
3、同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点,再往上回溯,发现 3 有除 6 以外的子点 7,所以此时会遍历 7
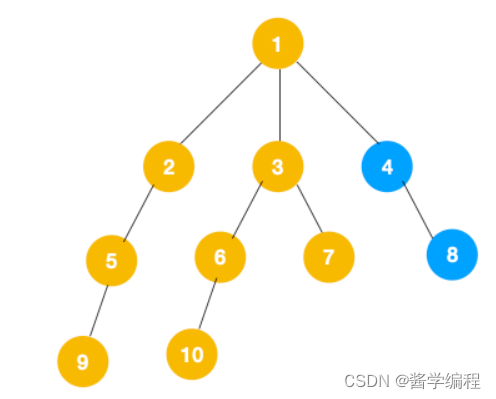
3、从 7 往上回溯到 3, 1,发现 1 还有节点 4 未遍历,所以此时沿着 4, 8 进行遍历,这样就遍历完成了
完整的节点的遍历顺序如下(节点上的的蓝色数字代表)
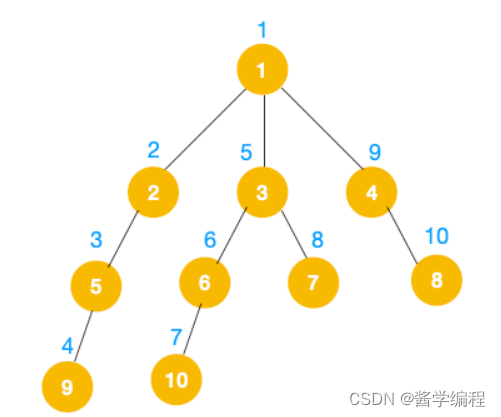
1.递归实现
public void dfs(TreeNode root){
if (root == null){
return;
}
System.out.println(root.val);
dfs(root.left);
dfs(root.right);
}
存在的问题:如果层次太深,容易造成栈溢出
2.非递归实现
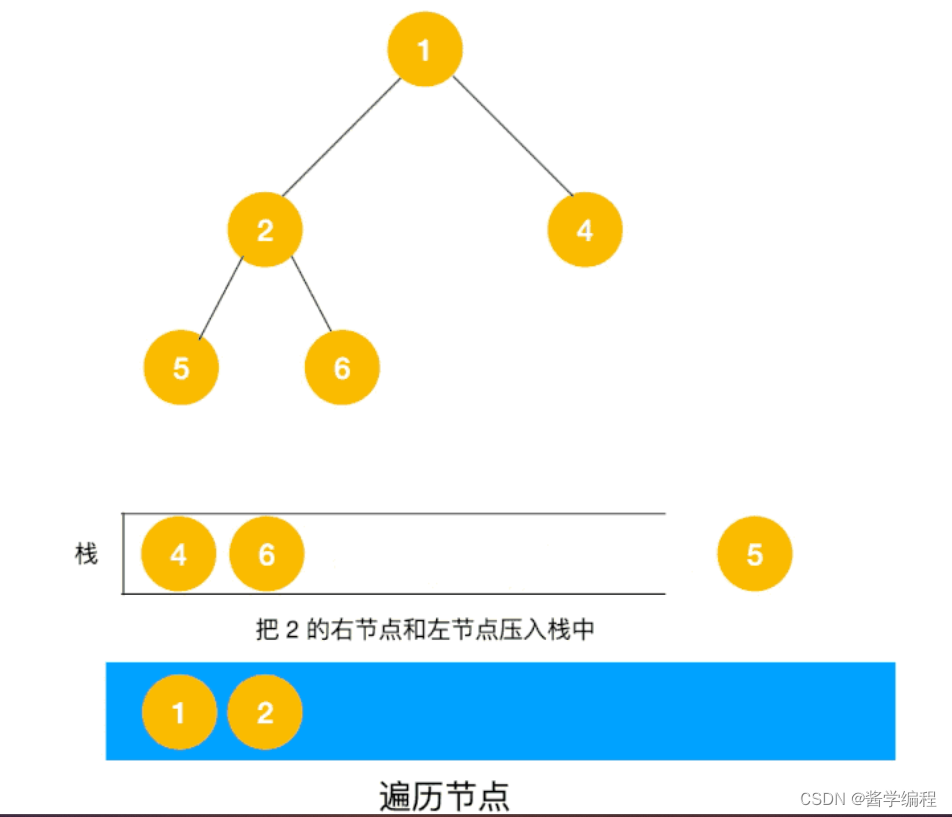
1.使用栈实现,对于每个节点,先遍历当前节点,然后吧右节点压栈,再压左节点。
2.弹栈,每弹出一个,重复1
每弹出一个节点,将这个节点的右节点和左节点放入栈,直到栈为空。
public void dfsTest02(TreeNode treeNode){
if (treeNode == null){
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.add(treeNode);
while (!stack.isEmpty()){
TreeNode peek = stack.pop();
System.out.println(peek.val);
if (peek.right != null){
stack.add(peek.right);
}
if (peek.left != null){
stack.add(peek.left);
}
}
}
BFS(breath first search) 广度优先遍历/层序遍历
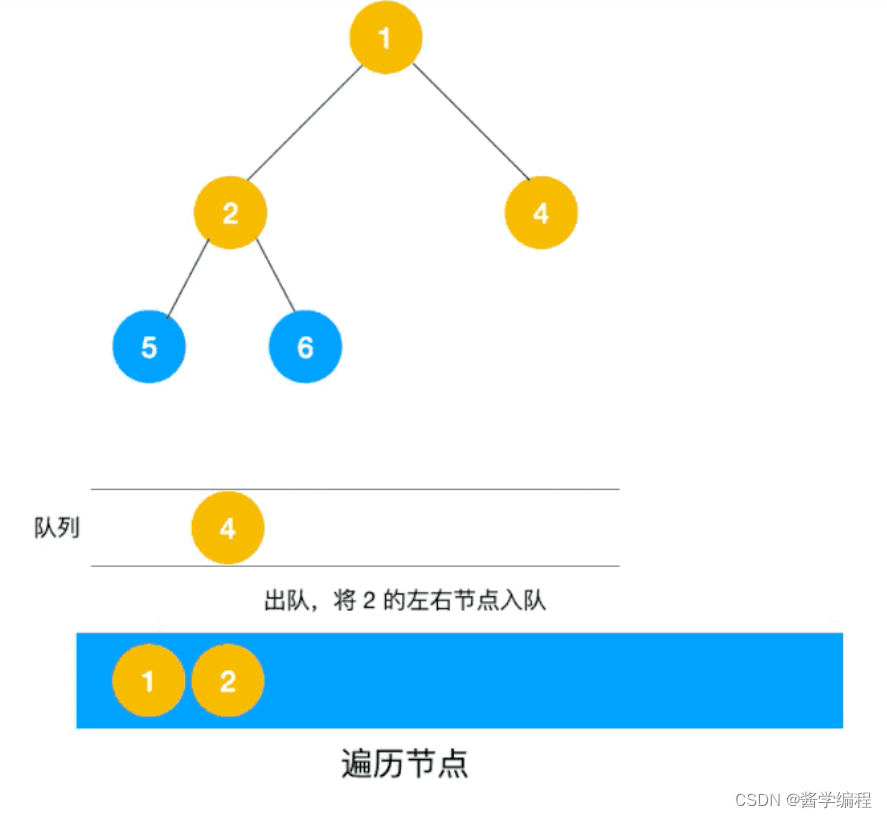
使用队列来实现,每次访问到的节点放入队列里面,每次从队头取一个节点,并将这节点的所有子节点存入队列,直到队列为空。
public void bfs(TreeNode root){
if (root == null){
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
TreeNode target = queue.poll();
System.out.println(target.val);
if (target.left != null){
queue.add(target.left);
}
if (target.right != null){
queue.add(target.right);
}
}
}
```