every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog

0. 前言

梳理有关自编码器

1. 自编码器

1.1 原理

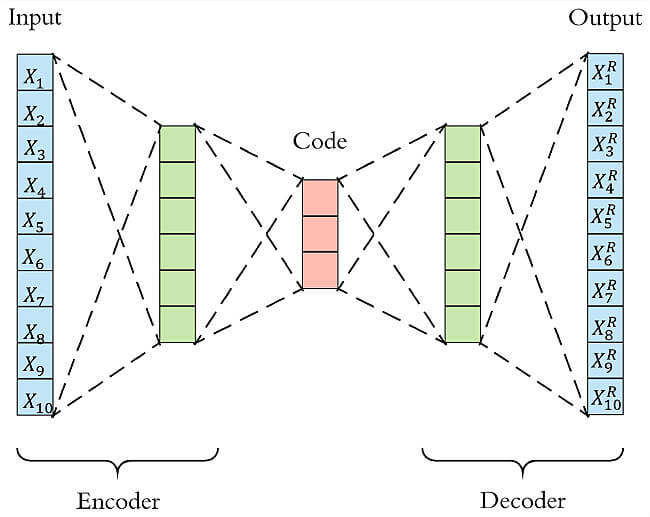
Auto-Encoder，中文称作自编码器，是一种无监督式学习模型。利用输入数据 $X$本身作为监督，来指导神经网络尝试学习一个映射关系，从而得到一个重构输出$X^R$ 。

可以用于异常检测场景，异常对于正常来说是少数，所以我们认为，如果使用自编码器重构出来的输出 $X^R$ 跟原始输入的差异超出一定阈值（threshold）的话，原始时间序列即存在了异常。和之前介绍的padim、patchcore等思想类似。

算法主要分为：encoder和decoder。

• 编码器的用于将高维输入$X$编码成低维的隐 变量$h$，从而强迫网络学习有用信息特征
• 解码器用于把隐变量$h$还原到初始维度，最好的状态是解码器的输出能够近似恢复原始输入。

如果输入神经元个数n大于隐藏层个数m,那么就相当于把数据从n维降到m维，类似PCA。

1.2 作用

• 特征学习：通过学习数据的有用表示，自动编码器可以用于特征学习任务，有助于提高监督学习模型的性能
• 降维：自动编码器可以将高维数据映射到低维空间，从而实现数据的降维，有助于可视化和减少计算复杂度
• 图像去噪：通过训练自动编码器来学习对输入数据的干净表示，可以用于去除图像中的噪声
• 生成模型：通过改变自动编码器的架构，可以设计生成对抗网络（GAN）等生成模型

1.3 demo

def getModel():
    input_layer = Input(shape=(x.shape[1],))
    encoded = Dense(8, activation='relu', activity_regularizer=regularizers.l2(10e-5))(input_layer)  # l2正则化约束
    decoded = Dense(x.shape[1], activation='relu')(encoded)
    autoencoder = Model(input_layer, decoded)
    autoencoder.compile(optimizer='adam', loss='mean_squared_error')
    return autoencoder 

2. 降噪自编码器

论文： Extracting and Composing Robust Features with Denoising Autoencoders

原理： 原始数据X上加入了噪声X’，然后再作为网络的输入数据，来重构输出原始还未加入噪声的数据。

因此降噪自编码的损失函数是构造原始数据X与网络输出X’'之间的一个差异性度量。加入噪声，然后训练恢复原始数据，可以让我们的网络具有更强的抗噪能力，使得自编码更加鲁邦。

通过对原始数据输入神经元，进行人为随机损坏加噪声，得到损坏数据X’。主要有：

• 采用高斯噪声
• 把输入神经元随机置0（类似dropout）

3. 稀疏自编码器

损失函数加入一个KL散度作为网络的正则约束项

4. 收缩自编码器

同样是修改损失函数，

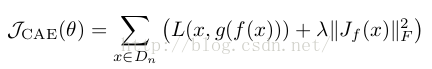
5. 栈式自编码器

开始讲什么是栈式自编码前，让我们先来了解一些深度学习中的无监督预训练。我们知道，在深度学习中，一般网络都有很多层，因为网络层数一多，训练网络采用的梯度下降，在低层网络会出现梯度弥散的现象，导致了深度网络一直不招人待见。直到2006年的3篇论文改变了这种状况，由Hinton提出了一种深层网络的训练方法，改变了人们对深度学习的态度。Hinton所提出的训练思想，整体过程如下；

A、网络各层参数预训练。我们在以前的神经网络中，参数的初始化都是用随机初始化方法，然而这种方法，对于深层网络，在低层中，参数很难被训练，于是Hinton提出了参数预训练，这个主要就是采用RBM、以及我们本篇博文要讲的自编码，对网络的每一层进行参数初始化。也就是我们这边要学的稀疏自编码就是为了对网络的每一层进行参数初始化，仅仅是为了获得初始的参数值而已（这就是所谓的无监督参数初始化，或者称之为“无监督 pre-training”）。

B、比如采用自编码，我们可以把网络从第一层开始自编码训练，在每一层学习到的隐藏特征表示后作为下一层的输入，然后下一层再进行自编码训练，对每层网络的进行逐层无监督训练。

C、当我们无监督训练完毕后，我们要用于某些指定的任务，比如分类，这个时候我们可以用有标签的数据对整个网络的参数继续进行梯度下降调整。

这就是深层网络的训练思想，总体归结为：无监督预训练、有监督微调。

OK，我们回到本篇文章的主题，从上面的解释中，我们知道稀疏自编码仅仅只是为了获得参数的初始值而已。栈式自编码神经网络是一个由多层稀疏自编码器组成的神经网络，其前一层自编码器的输出作为其后一层自编码器的输入。栈式自编码就是利用上面所说的：无监督pre-training、有监督微调进行训练训练的深度网络模型。接着就让我们来学一学具体的栈式自编码网络训练。

训练如下网络如下分类任务：

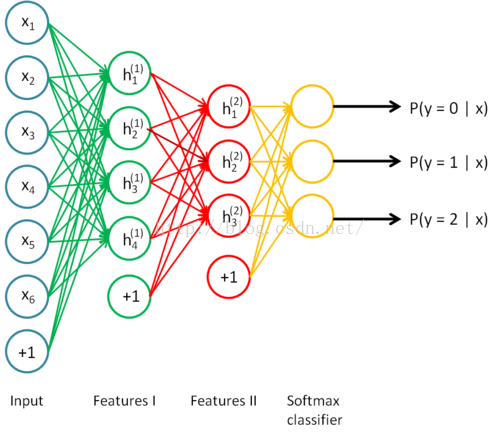
step1: 无监督pre-training阶段：

先采用自编码的方式，训练第一个隐藏层：

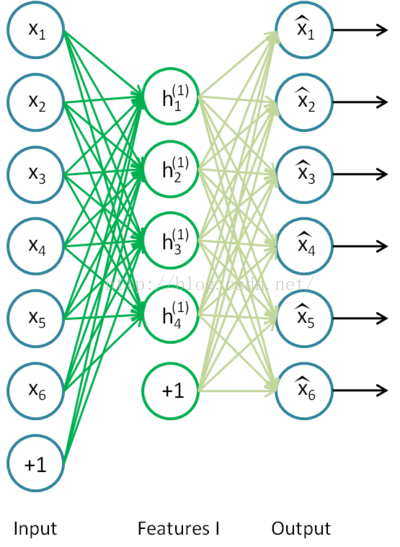
训练完以后，继续训练第二个隐藏层：

把h1作为输入，把h2作为隐藏层，然后进行自编码训练

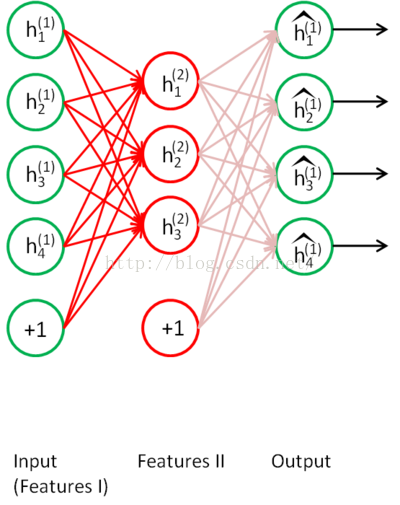
至此，我们对两个中间层的参数进行的训练初始化。

后面就是正常的网络训练了。

参考

1. https://blog.csdn.net/hjimce/article/details/49106869
2. http://sofasofa.io/tutorials/anomaly_detection/
3. https://blog.csdn.net/lijj0304/article/details/136269138
4. https://blog.csdn.net/liangjiubujiu/article/details/81286770
5. https://zhuanlan.zhihu.com/p/80377698
6. https://zhuanlan.zhihu.com/p/133207206
7. https://zhuanlan.zhihu.com/p/68903857