1 欧拉图
欧拉图是指通过图(无向图或有向图)中所有边且每边仅通过一次通路,
相应的回路称为欧拉回路。具有欧拉回路的图称为欧拉图(Euler Graph),
具有欧拉通路而无欧拉回路的图称为半欧拉图。
对欧拉图的一个现代扩展是蜘蛛图,它向欧拉图增加了可以连接的存在点。
这给予欧拉图析取特征。
欧拉图已经有了合取特征(就是说区定义了有着与起来的那些性质的对象在区中的存在)。
所以蜘蛛图允许使用欧拉图建模逻辑或的条件。
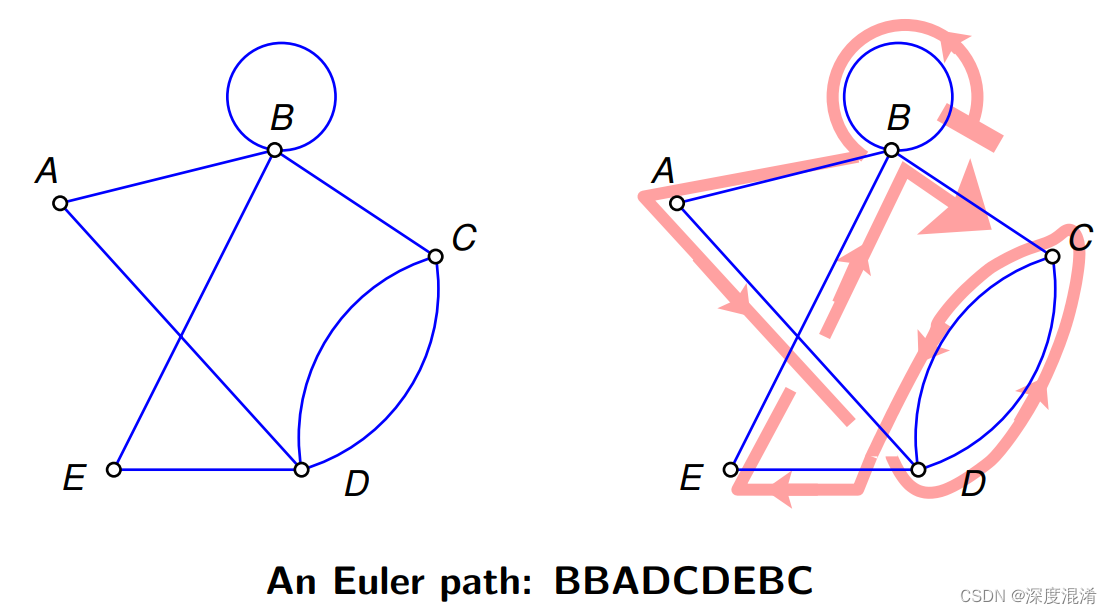
Euler图-如果有一条包含图G的每条边的闭合轨迹,则连通图G称为Euler图。
Euler路径-Euler路径是一条只使用图形的每条边一次的路径。Euler路径从不同的顶点开始和结束。
Euler回路-Euler回路是一个只使用图形的每条边一次的回路。Euler回路始终在同一顶点开始和结束。连通图G是Euler图当且仅当G的所有顶点都是偶数时,连通图G是Euler图当且仅当其边集可以分解为圈时。
参考: