一.P2089 烤鸡

算法思想： 指数型枚举，可以通过dfs深度优先搜索暴力枚举出所有可能的情况，在通过剪枝去除错误的方案来减少时间开销。主要用一个循环枚举每个调料放几克（每个位置的分支情况都相同），注意回溯时当前位置的置空。

#define N 15
int n;
int arr[N];//存临时方案
int mem[50000][N];//存正确的方案
int res = 0;//存方案数
//表示枚举到了第x位，sum表示此时调料的质量和
void dfs(int x, int sum)
{
    //sum不符，剪枝
    if (sum > n)
        return;
    //枚举完第10位后判断是否符合
    if (x > 10)
    {
        if (sum == n)
        {
            res++;
            for (int i = 1; i <= 10; i++)
            {
                mem[res][i] = arr[i];
            }
        }
        return;
    }
    for (int i = 1; i <= 3; i++)
    {
        //记录第x位上的调料质量
        arr[x] = i;
        dfs(x + 1, sum + i);
        //回溯，将调料质量置空
        arr[x] = 0;
    }
}

二.P1088 [NOIP2004 普及组] 火星人

 

算法思想： 排序型枚举，依旧dfs暴力枚举出每种排序，主要通过st[N]状态数组来记录每个数的选择情况，第x位选择状态为未选择的数并给该数设置已选择状态，然后枚举x+1位直至枚举完，判断是否符合，并根据具体情况进行剪枝。

#define N 10010

int n, a;
int mas[N];//存火星人初始值
int arr[N];//存符合条件的
bool st[N];//存每个数的状态
int cnt = 0;//记录增加的值
bool return0 = false;

//枚举到第x位
void dfs(int x)
{
    //剪枝
    if (return0)
    {
        return;
    }

    if (x > n)
    {
        cnt++;//初始值的cnt为1，则cnt为a+1时表示加上a后的排序
        if (cnt == a + 1)//注意是a+1!!!
        {
            return0 = true;//表示已经找到，直接使剩下的递归全部剪枝
            for (int i = 1; i <= n; i++)
            {
                printf("%d ", arr[i]);
            }
            printf("\n");
        }
        return;
    }
    //第x位上的手指不能枚举到已经存在于其他位置的手指（序号）
    for (int i = 1; i <= n; i++)
    {
        if (!cnt)
        {
            //使一开始从火星人初始值开始深搜
            i = mas[x];
        }
        //判断代号i的手指是否被选过
        if (!st[i])
        {
            st[i] = true;//表示第x位选i代号的手指，状态置为true,防止其他位置再次选择i；
            arr[x] = i;//存临时方案
            dfs(x + 1);//枚举下一位置
            arr[x] = 0;//回溯置空
            st[i] = false;//回溯重置i代号手指的状态，使其他位置可以选择i；
        }

    }
}

int main()
{
    scanf("%d %d", &n, &a);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &mas[i]);
    }
    dfs(1);

    return 0;
}

三.P1149 [NOIP2008 提高组] 火柴棒等式

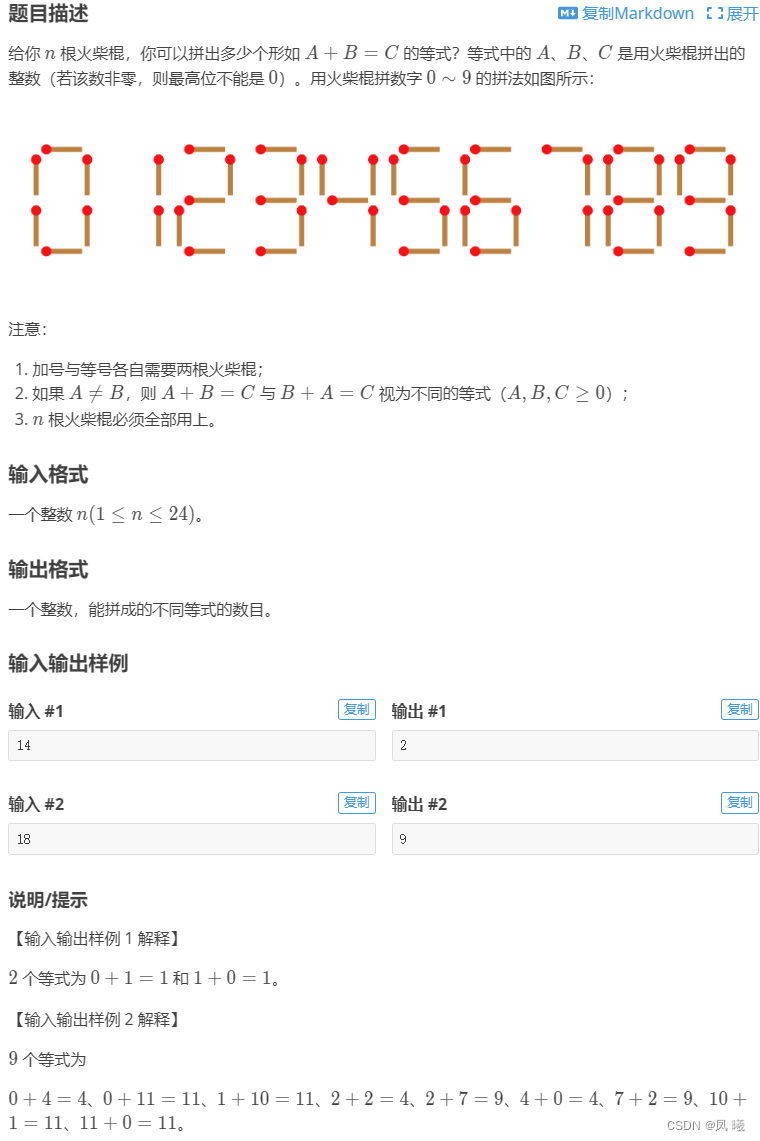
算法思想：指数型枚举，一共三个位置，先构造一个火柴用量数字表，根据表依次枚举每个位置的火柴表示数，最后符合火柴用量==n，数字等式成立两个条件后记录数+1，注意当火柴用量超出时剪枝。

#define N 1000

int firecout[N] = { 6,2,5,5,4,5,6,3,7,6 };//记录每个数所用火柴个数
int n;//可用的火柴总数
int res = 0;//记录方案数
int arr[10];//记录临时方案

//枚举到第x位，sum记录此时所用火柴数
void dfs(int x, int sum)
{
    if (sum > n) return;
    if (x > 3)
    {
        //枚举完三位后判断火柴等式是否成立
        if (arr[1] + arr[2] == arr[3]&& sum == n)
            res++;
        return;
    }
    for (int i = 0; i < N; i++)
    {
        //记录第x位的火柴表示数，便于最后的条件判断
        arr[x] = i;
        dfs(x + 1, sum + firecout[i]);
    }
}

int main()
{
    scanf("%d", &n);
    n -= 4;
    //记载个位数以外的数的所用火柴数
    for (int i = 10; i <= N; i++)
        firecout[i] = firecout[i / 10] + firecout[i % 10];
    dfs(1, 0);
    printf("%d", res);
    return 0;
}

 四.P1036 [NOIP2002 普及组] 选数

算法思想：组合型枚举，用dfs暴力枚举出所有组合情况，主要是通过设置一个start下标，使第x位以后的位置都不能枚举到start下标以前的数据，实现组合不重复的实现。通过算出x位以后可选的数是否最终能达到要求来剪枝。

#define N 25
int n, k;
int _begin[N];//存初始数组
int choice[N];//存临时选择数组
int res = 0;//存方案数

bool isPrimenum(int n)
{
    if (n < 2) return false;
    for (int i = 2; i <= n / i; i++)
    {
        if (n % i == 0)
            return false;
    }
    return true;
}
//x为枚举到的位置,start为选择初始数的位置(选组合数)
//start前的数，第x位及其以后的位都不会选到（避免重复）。
void dfs(int x, int start)
{
    //剪枝，x-1为已选位置的个数，n-start+1为剩下的可选个数
    if (x - 1 + n - start + 1 < k) return;
    if (x > k)
    {
        //已选k个数的和判断是否为质数（判断结果）
        int sum = 0;
        for (int i = 1; i <= k; i++)
        {
            sum += choice[i];
        }
        if (isPrimenum(sum))
        {
            res++;
        }
        return;
    }
    //组合型枚举的核心，第x位从start开始，保证组合不重复
    for (int i = start; i <= n; i++)
    {
        choice[x] = _begin[i];//存第x位的数
        dfs(x + 1, i + 1);//开始选择第x+1位的数
        choice[x] = 0;//回溯置空
    }
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &_begin[i]);
    }
    dfs(1, 1);//从第1位开始枚举
    printf("%d", res);
    return 0;
}