原题链接:2617. 网格图中最少访问的格子数
题目描述:
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
- 满足
j < k <= grid[i][j] + j的格子(i, k)(向右移动),或者 - 满足
i < k <= grid[i][j] + i的格子(k, j)(向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
输入输出描述:
示例 1:
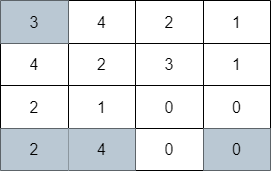
输入:grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]] 输出:4 解释:上图展示了到达右下角格子经过的 4 个格子。
示例 2:

输入:grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]] 输出:3 解释:上图展示了到达右下角格子经过的 3 个格子。
示例 3:
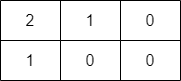
输入:grid = [[2,1,0],[1,0,0]] 输出:-1 解释:无法到达右下角格子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10^51 <= m * n <= 10^50 <= grid[i][j] < m * ngrid[m - 1][n - 1] == 0
解题思路:
这个题目我觉得出的非常好,一个非常经典的单调栈优化dp,这个题目首先每一步只能往右或者下走,很容易看出是dp,但是如果直接暴力dp,对于每个位置每次最多从n或者m个位置转移过来,那么时间复杂度就是O(n*m*(n+m)),这个时间复杂度就有点高了,我们需要考虑优化,我觉得有意思的就是这个优化,很容易可以看出需要维护的是某个区间的最小值,那么最容易想到的就是滑动窗口优化,但是这里左窗口虽然是单调减小的,但是右窗口的单调性不稳定,所以这个时候如果使用滑动窗口优化就不方便了,实际上我们考虑单调栈进行维护,我们考虑倒序枚举,在单调栈中维护一个从栈底到栈顶单调递增的序列,我们需要对每一行和每一列都维护一个单调栈,我们需要找到当前行中<=j+grid[i][j]的中的最小值,也就是需要找到从栈底到栈顶第一个列位置<=j+grid[i][j]的位置的值,我们直接在单调栈上进行二分即可,对于列做同样的处理即可。
通过上面的分析,这个问题就可以解决了,但是我写出了一个bug找了很久才找出来,那就是在单调栈维护的过程中,我们需要将行和列都更新完f[i][j]之后,才能进行去维护单调栈,因为如果我们只更新完行就去维护单调栈,但是后面更新列的时候f[i][j]又变小了,那么会导致行单调栈中的还有一些元素需要删除的没有删掉,导致后面某些位置计算到了一些错误的答案,对于只更新完列就去维护单调栈同样会出现这种错误,所以我们只有当行和列都更新完,才能去维护单调栈,这个错误我是真的看了好久才看出来,开始根本没有注意到这一点,就是一直是错的,但是我又确信我的思路应该是没有什么问题的,也就是突然之间就灵机一动意识到了这一点,不然我可能还真很难找到这个错误。
时间复杂度:O(n*m*(log(n)+log(m)))。
空间复杂度:O(n*m)。
cpp代码如下:
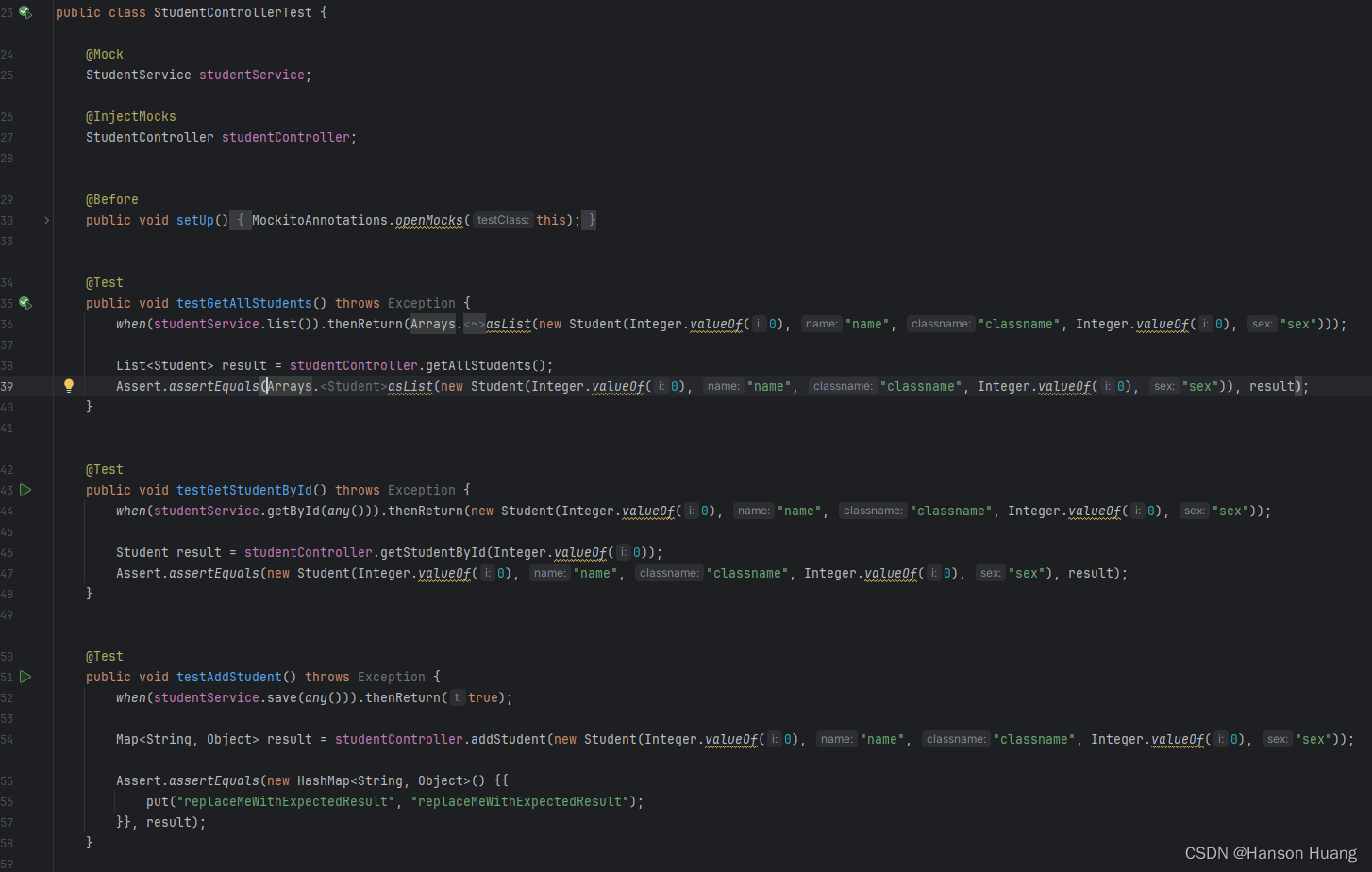
class Solution {
public:
int minimumVisitedCells(vector<vector<int>>& grid) {
int n=grid.size(),m=grid[0].size();
vector<int>row[n],col[m];
vector<vector<int>>f(n,vector<int>(m,1e9));
f[n-1][m-1]=1;
for(int i=n-1;i>=0;i--)
for(int j=m-1;j>=0;j--)
{
int l=0,r=row[i].size()-1;
while(l<r){
int mid=l+r>>1;
if(row[i][mid]<=j+grid[i][j])r=mid;
else l=mid+1;
}
if(r>=0 && row[i][r]<=j+grid[i][j]){
f[i][j]=min(f[i][j],f[i][row[i][r]]+1);
}
l=0,r=col[j].size()-1;
while(l<r){
int mid=l+r>>1;
if(col[j][mid]<=i+grid[i][j])r=mid;
else l=mid+1;
}
if(r>=0 && col[j][r]<=i+grid[i][j]){
f[i][j]=min(f[i][j],f[col[j][r]][j]+1);
}
//上面行和列都更新完才来维护单调栈
while(row[i].size() && f[i][row[i].back()]>=f[i][j]){
row[i].pop_back();
}
while(col[j].size() && f[col[j].back()][j]>=f[i][j]){
col[j].pop_back();
}
row[i].push_back(j);
col[j].push_back(i);
}
if(f[0][0]==1e9)return -1;
return f[0][0];
}
};