(1)抓奶牛问题描述:
农夫约翰被告知逃跑的奶牛的位置,并且要求立即去抓住它。约翰开始的位置在数轴上位置 N ( 0 ≤ N ≤ 100) ,而奶牛的位置在同样一个数轴上的 K (0 ≤ K ≤ 100) 。约翰有两种移动方式:步行和瞬间移动。
- 步行 : 从任意一点 X 移动到 X+1 或者 X-1 ,花一分钟。
- 瞬间移动 : 从任意一点 X 移动到 2X ,花一分钟。
如果奶牛没有意识到被抓捕,也就不会移动,过多久农夫会抓到奶牛?
输入
一行:用空格分开的两个整数: N 和 K
输出
一行 : 农夫抓到奶牛需要的最少分钟数。
例子输入
5 17
例子输出
4(农夫最快的抓捕路径是 5-10-9-18-17, 用时 4 分钟)
建立抓奶牛问题的解题思路
农夫和奶牛的距离是我们判断农夫抓住奶牛的依据,我们是可以很容易得到的,但农夫每一次都有3种选择,X+1,X-1,2X我们都要考虑并把每种情况发生后农夫与奶牛的距离记录下来,在做了这次选择后还没有抓住奶牛的话,再继续考虑下一个3种选择,在这个过程中,我们相当于搜索一颗完全的3叉树,但我们可以剪掉一些枝叶,例如在农夫的位置大于奶牛的位置的时候我们就不可能再去搜索它的下一层的X+1和2X的位置,如果这样就只能越来越远了。在搜索中程序第一次搜索到农夫与奶牛的距离为0时结束,这表示农夫抓住了奶牛。
分枝限界法与解空间树的广度优先遍历算法极为相似。唯一的不同之处是分枝限界法不搜索以不可行结点为根的子树。
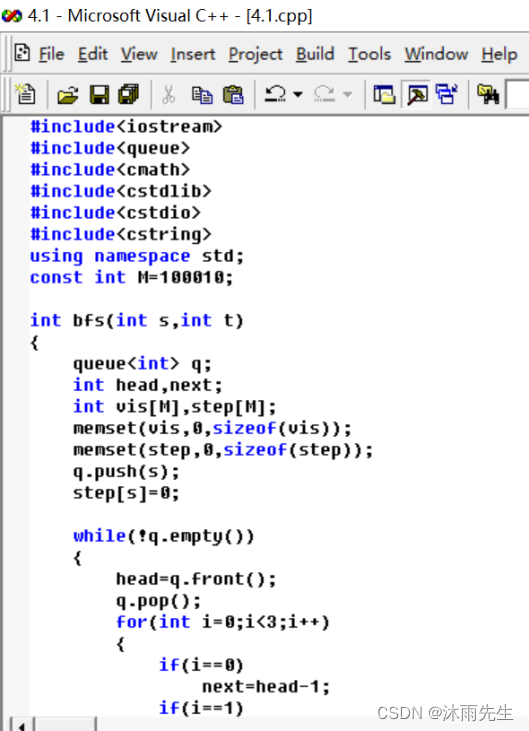
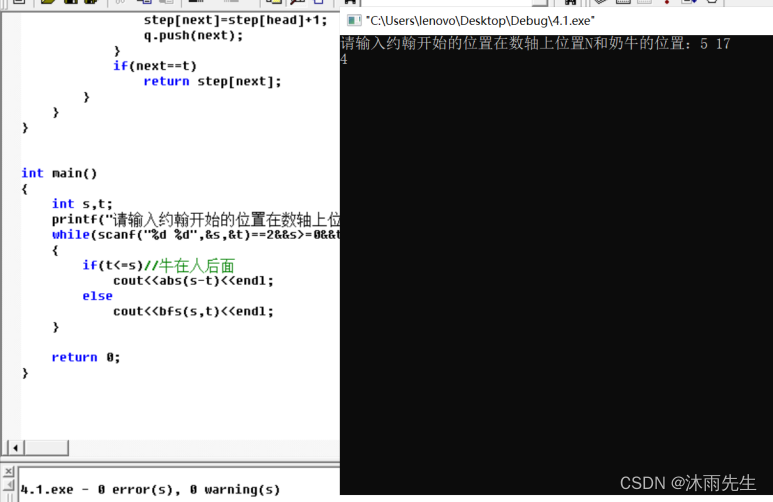
程序截图
(2)实验题目: 部落卫队问题
原始部落 Byteland 中的居民们为了争夺有限的资源,经常发生冲突。几乎每个居民都有他的仇敌。部落酋长为了组织一支保卫部落的队伍,希望从部落的居民中选出最多的居民入伍,并保证队伍中任何两个人都不是仇敌。
[ 输入说明 ]
第一行给出居民数 n 和仇敌关系数 m ;下面的 m 行给出每一个仇敌关系,仇敌关系 u 和 v 表示居民 u 和 v 是仇敌。
[ 输出说明 ]
第一行给出部落卫队人数,第二行是卫队组成, 1 代表对应居民在卫队中, 0 代表对应居民不在卫队中
[ 分支限界法分析 ]
把部落的每个人看作是无向图的一个顶点 , 敌对关系看作是无向图的一条边 , 因此 , 该问题可以转化为求一个无向图顶点数最多的独立集 。而分支限界法是基于广度优先的搜索算法,根据广度优先算法的最优性可知,分支限界法一定可以得出一个无向图顶点数最多的独立集。
[ 参考输入、输出、结果 ]
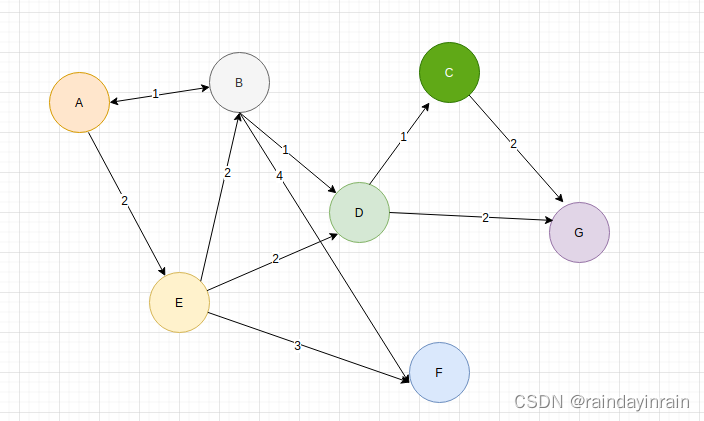
输入 :部落人数: 7
敌对关系数: 10
敌对关系为 : 1 , 2 1,4 2,3 2,4 2,5 2,6 3,5 3,6 4 ,5 5,6
输出 :卫队人数为:3
卫队成员为【1,0,1,0,0,0,1】
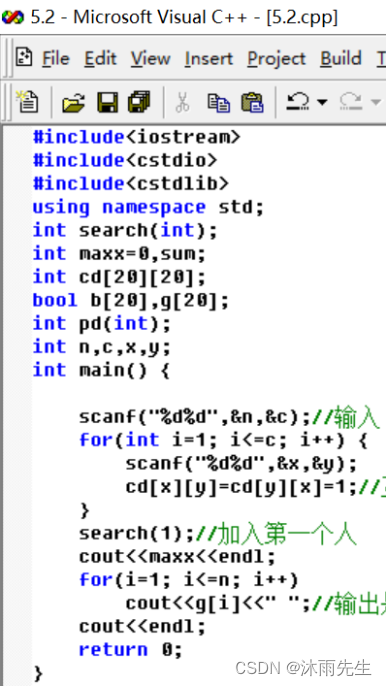
源程序
(1)
###include<iostream>
#include<queue>
#include<cmath>
#include<cstdlib>
#include<cstdio>
#include<cstring>
using namespace std;
const int M=100010;
int bfs(int s,int t)
{
queue<int> q;
int head,next;
int vis[M],step[M];
memset(vis,0,sizeof(vis));
memset(step,0,sizeof(step));
q.push(s);
step[s]=0;
while(!q.empty())
{
head=q.front();
q.pop();
for(int i=0;i<3;i++)
{
if(i==0)
next=head-1;
if(i==1)
next=head+1;
if(i==2)
next=head*2;
if(next<0||next>M)
continue;
if(vis[next]==0)
{
vis[next]++;
step[next]=step[head]+1;
q.push(next);
}
if(next==t)
return step[next];
}
}
}
int main()
{
int s,t;
printf("请输入约翰开始的位置在数轴上位置N和奶牛的位置:");
while(scanf("%d %d",&s,&t)==2&&s>=0&&t<=M)
{
if(t<=s)//牛在人后面
cout<<abs(s-t)<<endl;
else
cout<<bfs(s,t)<<endl;
}
return 0;
}
(2)
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int search(int);
int maxx=0,sum;
int cd[20][20];
bool b[20],g[20];
int pd(int);
int n,c,x,y;
int main() {
scanf("%d%d",&n,&c);//输入
for(int i=1; i<=c; i++) {
scanf("%d%d",&x,&y);
cd[x][y]=cd[y][x]=1;//互相是敌人标记1
}
search(1);//加入第一个人
cout<<maxx<<endl;
for(i=1; i<=n; i++)
cout<<g[i]<<" ";//输出是否加入
cout<<endl;
return 0;
}
int search(int x) {
for(int i=1; i<=n; i++) {
if(!b[i]) { //没有加入
if(pd(i)) { //判断已经加入的人中是否有他的仇敌
b[i]=1; //加入队伍,加入的人数加1
sum++;
}
if(x==n) { //全都加完
if(sum>maxx)
maxx=sum;//找最大值
for(int i=1; i<=n; i++)
g[i]=b[i];//记录答案
} else {
search(x+1);//找下一个
b[i]=0;//回溯(回溯注意在else里)
sum--;
}
}
}
return 0;
}
int pd(int x) {
for(int i=1; i<=n; i++) {
if(b[i]&&cd[x][i])//判断与已经加入的人是否是仇敌
return 0;
}
return 1;
}