自动驾驶---Motion Planning之轨迹Path优化

news2024/9/27 5:45:09

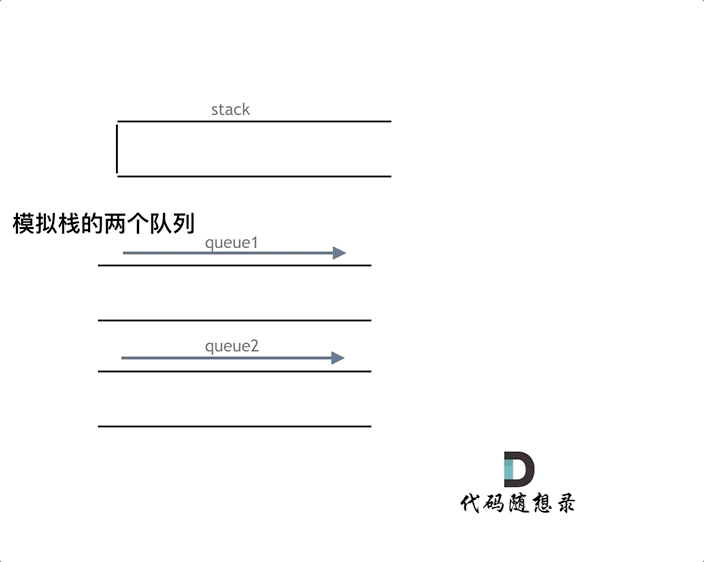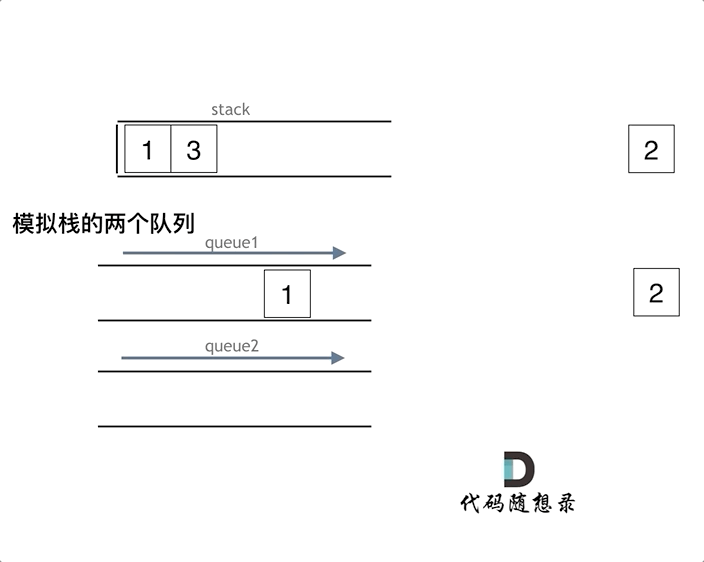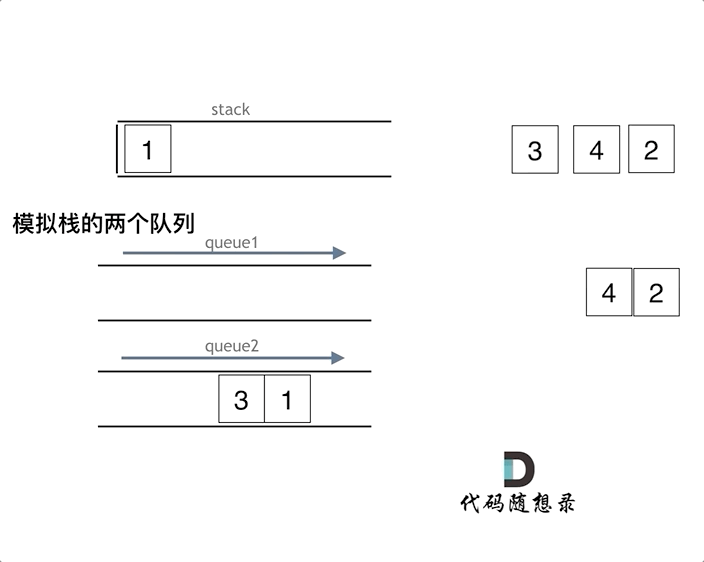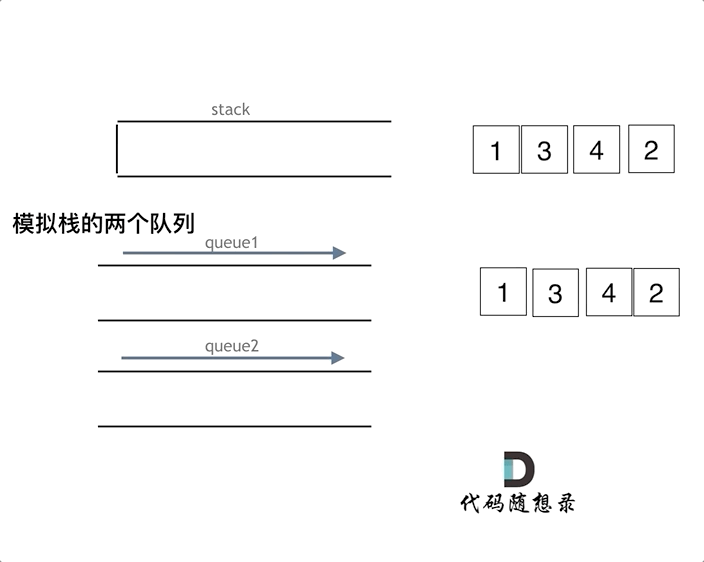
1 背景

在之前的几篇文章中，不管是通过构建SL图《自动驾驶---Motion Planning之Path Boundary》，ST图《自动驾驶---Motion Planning之Speed Boundary》，又或者是构建SLT图《自动驾驶---Motion Planning之构建SLT Driving Corridor》，最终我们都是为了得到boundary的信息。

构造优化问题求解的前提：首先确定问题的代价函数，有初值，有边界（约束），然后进行求解。笔者会先阐述Apollo中轨迹横纵向优化的问题，接下来会在后面的博客中继续讲解STSC中的轨迹优化问题。

2 轨迹横向优化

总体流程图以车道保持场景为例子进行说明。task的主要功能位于Process()函数中。规划模块的运动总体流程图如下：

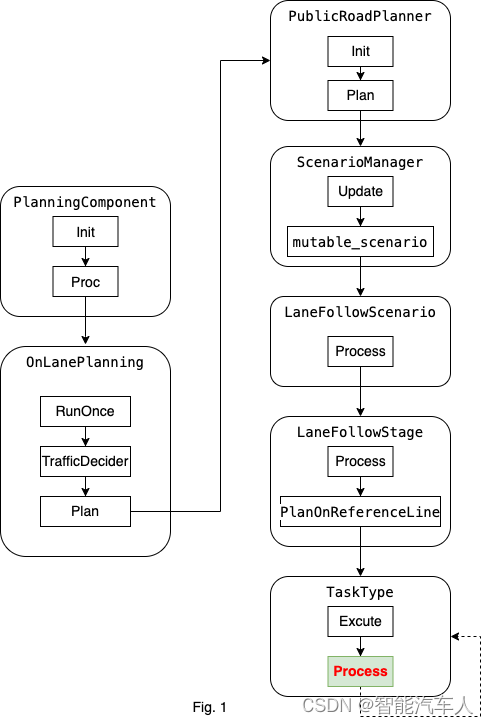
首先有一点值得注意：在Apollo中，横纵向的优化求解是解耦开的，因此在横纵向分别需要求解一次，最终得到得到横纵向的轨迹信息（s，s'，s''，l，l'，l''）------这里的 $eq?l%27$ 是 $eq?l$ 关于 $eq?s$ 的一阶导数， $eq?s%27$ 是 $eq?s$ 关于 $eq?t$ 的一阶导数。

整体轨迹优化器的代码位于/apollo/modules/planning/tasks/optimizers。

见到下图，看过笔者之前的博客《自动驾驶---Motion Planning之参考线Path平滑》就非常熟悉了，之前在参考线平滑中详细讲解了这部分的内容。

但是这次与参考线平滑不同的是：代价函数的定义。本篇博客主要讲解横向Path的优化过程，在下一篇为读者讲解纵向Speed的优化过程。

二次规划问题的形式：

$eq?min%28%5Ccfrac%7B1%7D%7B2%7Dx%5ETHx+g%5ETx%29%20%5C%5C%20%5C%5C%20s.t.%20a_i%5ETx%20%3D%20b_i%2C%20i%5Cin%7BE%7D%20%5C%5C%20h_j%5ETx%5Cle%7Bt_j%7D%2C%20j%5Cin%7BI%7D$

其中 $eq?H$ 是由二阶导构成的Hessian矩阵， $eq?g%5ET$ 是由梯度构成的Jacobi矩阵；然后包括m个等式约束集合和n个不等约束集合。

Path优化问题的自变量为： $eq?x%3D%5Bl_0%2Cl_1...l_%7Bn-1%7D%2Cl%27_0%2Cl%27_1%2Cl%27_2...l%27_%7Bn-1%7D%2Cl%27%27_0%2Cl%27%27_1...l%27%27_%7Bn-1%7D%5D$ 。

2.1.1 优化目标

优化目标中主要考虑了：1）横向位移；2）横向速度；3）横向加速度；4）横向Jerk；5）障碍物的距离。

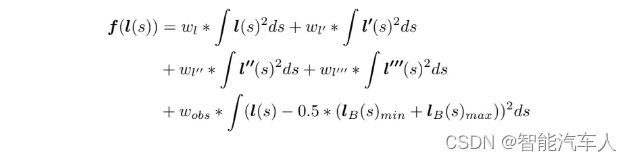
（注意：论文这里的代价函数与Apollo源码中有些差异，源码中没有考虑障碍物，而是增加了更接近参考点的代价以及终点的代价）

$%5CDelta%20s%29%5E2+w_%7Blend%7D%28l_%7Bn-1%7D-%20l_%7Bendl%7D%29%5C%5C%5C%5C+w_%7Bl%27end%7D%28l%27_%7Bn-1%7D-l%27_%7Bendl%7D%29+w_%7Bl%27%27end%7D%28l%27%27_%7Bn-1%7D-l%27%27_%7Bendl%7D%29$

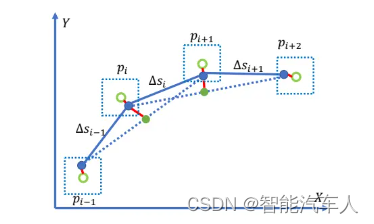
这里提到了一个概念：分段加加速度。为了有效地制定优化问题并在实践中评估约束满意度，论文中根据空间参数 $eq?s$ 将路径函数 $eq?l%28s%29$ 离散到一定的分辨率 $eq?%5CDelta%20s$ ，并使用这些离散点来控制路径的形状，并近似地评估约束满意度。关键思想是将一维函数离散到二阶导数，并使用常数的三阶导数项来“连接”连续的离散点。位置变量的三阶