算法系列--动态规划--子序列(2)

news2024/11/16 1:49:13

💕"你可以说我贱，但你不能说我的爱贱。"💕
作者：Mylvzi
文章主要内容：算法系列–动态规划–子序列(2)

今天带来的是算法系列--动态规划--子序列(2),包含了关于子序列问题中较难的几道题目(尤其是通过二维状态表示来推导状态转移方程)

1.最⻓定差⼦序列

链接:
https://leetcode.cn/problems/longest-arithmetic-subsequence-of-given-difference/description/
在这里插入图片描述
分析:

状态表示:dp[i]:以i为结尾的,最长的定差子序列的长度
状态转移方程:if(hash.contains(a - difference)) dp[i] = dp[k] + 1
优化:由于要寻找a-difference与其对应的下标k,所以我们可以利用一个哈希表来建立数值与下标之间的映射关系

在这里插入图片描述

代码:

class Solution {
    public int longestSubsequence(int[] arr, int difference) {
        Map<Integer,Integer> hash = new HashMap<>();
        int ret = 1;// 记录最值

        for(int a : arr) {
            hash.put(a,hash.getOrDefault(a-difference, 0 ) + 1);// 将当前位置插入到哈希表中
            ret = Math.max(ret,hash.get(a));// 更新最值
        }

        return ret;
    }
}

2.最⻓的斐波那契⼦序列的⻓度

链接:
https://leetcode.cn/problems/length-of-longest-fibonacci-subsequence/

分析:
在这里插入图片描述

代码:

class Solution {
    public int lenLongestFibSubseq(int[] nums) {
        int n = nums.length;
        int[][] dp = new int[n][n];

        // 初始化为2
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) dp[i][j] = 2;
        }

        Map<Integer,Integer> hash = new HashMap<>();
        for(int i = 0; i < n; i++) hash.put(nums[i], i);// 将数组中的值和下标存入到哈希表之中
        hash.put(nums[0],0);
        int ret = 2;

        // 填表
        for(int j = 1; j < n; j++) {
            for(int i = 0; i < j; i++) {
                int a = nums[j] - nums[i];// 得到前一个位置的数
                if(a < nums[i] && hash.containsKey(a)) {//必须包含 且下标在i之前
                    dp[i][j] = dp[hash.get(a)][i] + 1;// 更新
                }

                ret = Math.max(ret,dp[i][j]);// 更新最值
            }
        }

        return ret < 3 ? 0 : ret;// 处理极端情况(无fib数列)
    }
}

3.最⻓等差数列

链接:
https://leetcode.cn/problems/longest-arithmetic-subsequence/description/

在这里插入图片描述

分析:
这道题笔者最开始经过分析,认为这道题和最长的斐波那契子序列的解法相同,同样的是利用固定两个数的方式来确定完整的等差数列,但是并未通过,反思如下:

最长的斐波那契子序列这道题目中,题目明确了整个序列是严格递增的,但是本题并没有这样的要求.这就加大了本题的难度,如果是严格递增的,就不需要考虑值重复的问题,但本题需要考虑,此时就需要使用<key,下标数组>这样的方式来保存值与下标之间的映射关系,在获取最长的长度时,我们需要的离倒数第二个数最近的元素的下标(此时的dp表中对应的长度是最长的),所以在得到nums[i] - nums[j]之后,还需要去便利整个下标数组,拿到最大的下标,进而获得最大的长度
上述方式固然是一种解决方案,但是时间复杂度也很高,优化策略:一边dp,一边保存离nums[i]最近的值的下标
如何实现上述策略呢?要想实现上述策略,需要我们在填表的时候采用固定倒数第二个数,枚举后一个数的方式,这样能保证我们获取到的a是离nums[i]最近的位置

代码:

class Solution {
    public int longestArithSeqLength(int[] nums) {
        int n = nums.length;
        int[][] dp = new int[n][n];

        // 初始化为2
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) dp[i][j] = 2;
        }

        Map<Integer,Integer> hash = new HashMap<>();
        hash.put(nums[0],0);

        int ret = 2;

        // 填表
        for(int i = 1; i < n; i++) {
            for(int j = i + 1; j < n; j++) {
                int a = 2 * nums[i] - nums[j];// 得到前一个位置的数
                if(hash.containsKey(a)) {//必须包含 且下标在i之前
                    dp[i][j] = dp[hash.get(a)][i] + 1;// 更新
                }

                ret = Math.max(ret,dp[i][j]);// 更新最值
            }

            hash.put(nums[i],i);
        }

        return ret;

    }
}

另一种状态表示:

上述需要固定两个数的原因在于无法通过一个数直接找到一个完整的等差序列,更本质的原因在于我们不知道公差究竟是多少,但是我们可以将i位置对应的所有公差都存入到dp表之内,这样就能枚举所有的d的情况,所以我们可以使用以i位置为结尾,公差为d的最长的等差序列的长度

class Solution {
    public int longestArithSeqLength(int[] nums) {
  
        int n=nums.length;
        int[][] dp=new int[n][1001];
        int maxLen=0;//保存结果
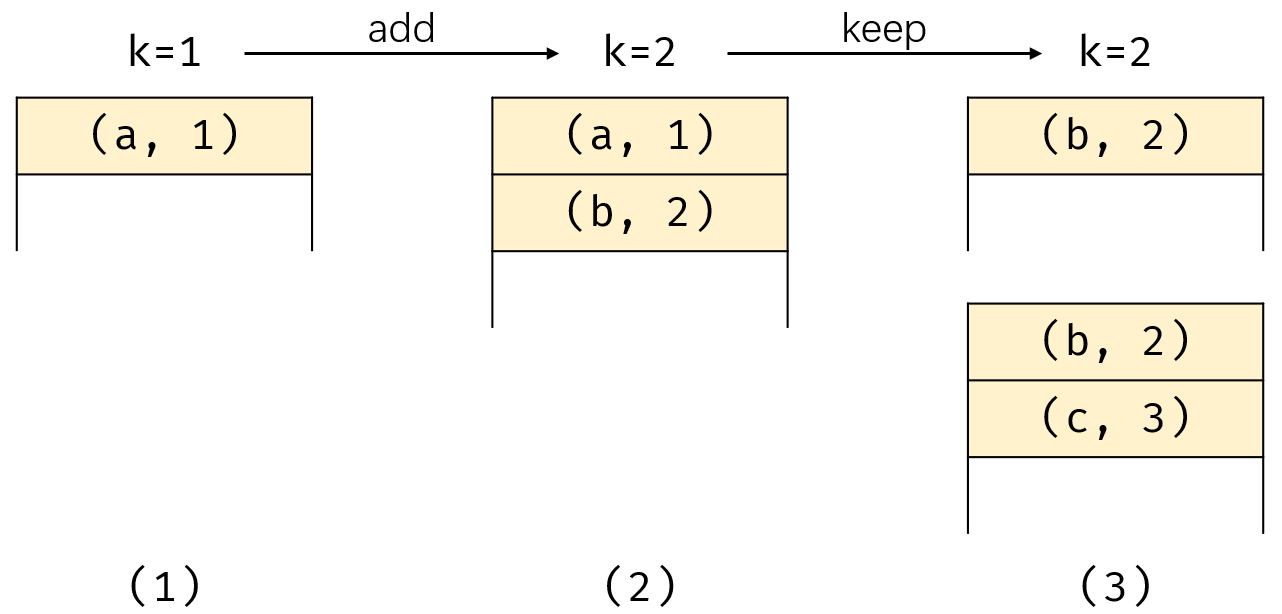
        for(int k=1;k<n;k++){
            for(int j=0;j<k;j++){
                int d=nums[k]-nums[j]+500;//统一加偏移量，使下标非负
                dp[k][d]=dp[j][d]+1; //根据 d 去填充dp[k][d]
                maxLen=Math.max(maxLen,dp[k][d]);//维护最大值
            }
        }
        return maxLen+1;
    }
}

但是笔者觉得第二种写法并不是特别好,有点投机取巧之嫌(其实只要能做出来就好)

4.等差数列划分II - ⼦序列

链接:
https://leetcode.cn/problems/arithmetic-slices-ii-subsequence/description/
在这里插入图片描述

分析:

之前做过等差数列划分I,那道题是子数组,强调必须是连续的,但是本题是子序列,是可以不连续的
如果做过上面的第二道题最长的等差序列,本题其实很容易想到思路,同样的,由于之定义一个状态无法表示确定状态,所以需要两个状态
dp[i][j]:以i,j位置(i < j)为结尾的所有等差数列的个数
思路和最长的等差序列也是相似的,首先固定倒数第一个数,接着从0遍历第二个数,找到符合条件的值后,获得其对应的下标,进而获得dp表中的值
一分析觉得这道题和最长的等差序列那道题很像,但是那道题只用保存最长的长度就行,这道题需要用一个数组保存相同值的所有下标,所以在哈希表中建立的映射关系应该是<key,int[]>(笔者想到了这点,但是不知道怎么表示int[],导致此题没做出来,惭愧惭愧),实际上只要存储一个List就行,遍历的时候使用for each遍历即可

代码:

class Solution {
    private int ret;// 返回值
    public int numberOfArithmeticSlices(int[] nums) {
        int n = nums.length;
        int[][] dp = new int[n][n];

        // 存放值与相同值的所有下标(下标应该是一个下标数组)
        Map<Long,List<Integer>> hash = new HashMap<>();
        for(int i = 0; i < n; i++) {
            long tmp = (long)nums[i];
            if(!hash.containsKey(tmp))
                hash.put(tmp,new ArrayList<Integer>());
            hash.get(tmp).add(i);
        }

        for(int j = 2; j < n; j++) {
            for(int i = 1; i < j; i++) {
                long a = 2L * nums[i] - nums[j];
                if(hash.containsKey(a)) {
                    // 遍历下标数组(注意相同的一个值的下标有多个,而我们要求出所有的等差序列的个数,所以所有的下标都要加上)
                    for(int k : hash.get(a)) {
                        if(k < i) dp[i][j] += (dp[k][i] + 1);// +1表示的是 k,j,i三个数字组成一个新的等差数列
                        else break;
                    }
                }

                ret += dp[i][j];// 计算当前位置的和
            }
        }
        
        return ret;
    }
}