长度最小子数组

题目：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续

子数组

[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

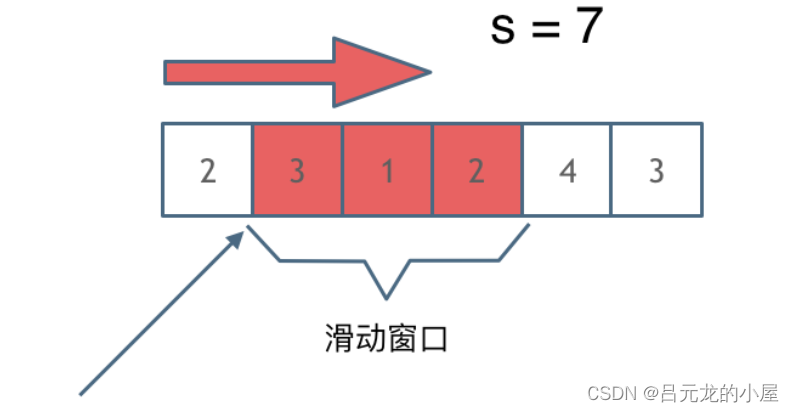
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

方法一：暴力破解，就是使用两个指针，一个指针固定，一个指针扫描，当扫描到的值大于等于target时记录。代码如下：

func minSubArrayLen(target int, nums []int) int {
	Len := len(nums)
	s, f := 0, 0
	sum := 0
	num := 0
	for s < Len {
		for sum < target {
			if f >= Len {
				return num
			}
			if num != 0 && f >= s+num {
				break
			}
			sum += nums[f]
			f++
		}
		if sum >= target {
			num = f - s
		}
		sum = 0
		s++
		f = s
	}
	return num
}

两个for循环，时间复杂度O(n²)

方法二：滑动窗口

func minSubArrayLen(target int, nums []int) int {
	Len := len(nums)
	f, r := 0, 0
	sum := 0
	num := 0
	for f < Len || sum >= target {
		if sum >= target {
			if (num != 0 && (f-r) < num) || num == 0 {
				num = f - r
			}
			sum -= nums[r]
			r++
		} else {
			sum += nums[f]
			f++
		}
		fmt.Println("r,f,sum", r, f, sum)
	}
	return num
}

一个循环搞定，时间复杂度降至O(n)。

想要学习滑动窗口相关知识，可以去看代码随想录 (programmercarl.com)。