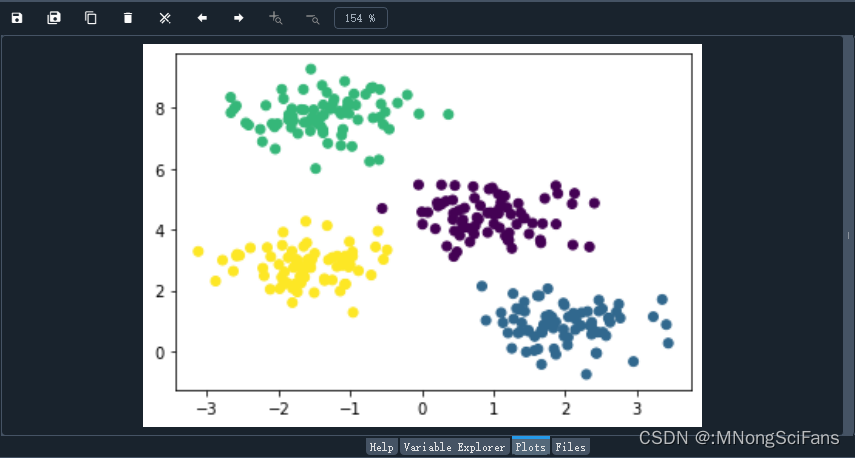
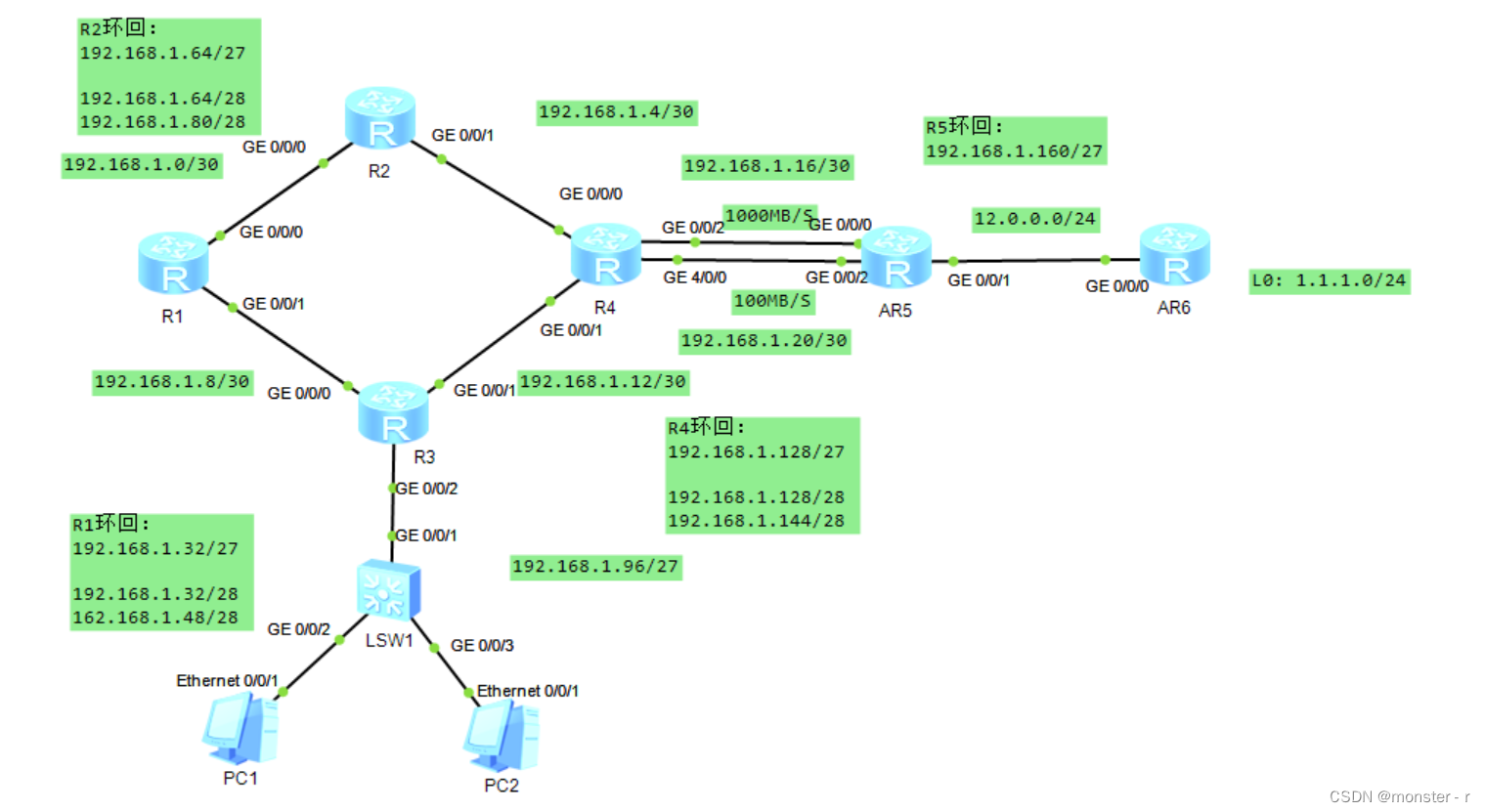
在机器学习中,无监督学习一直是我们追求的方向,而其中的聚类算法更是发现隐藏数据结构与知识的有效手段。聚类是一种包括数据点分组的机器学习技术。给定一组数据点,我们可以用聚类算法将每个数据点分到特定的组中。
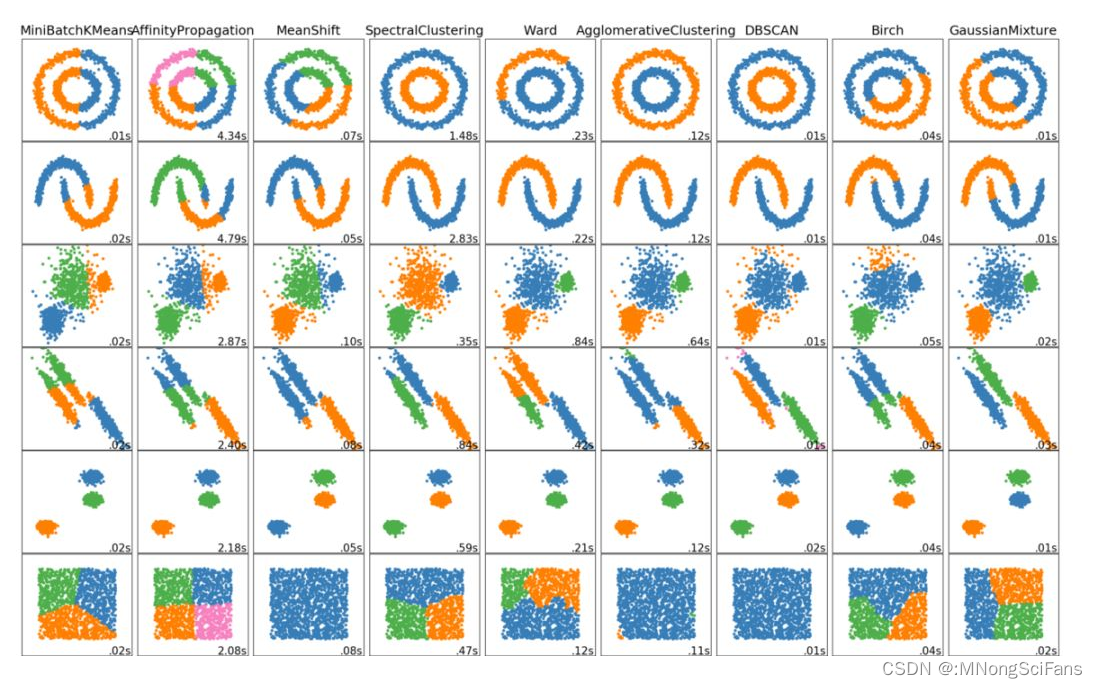
理论上,属于同一组的数据点应该有相似的属性和/或特征,而属于不同组的数据点应该有非常不同的属性和/或特征。聚类是一种无监督学习的方法,是一种在许多领域常用的统计数据分析技术。
K-Means(K 均值)聚类
KMeans聚类与分类、序列标注等任务不同,聚类是在事先并不知道任何样本标签的情况下,通过数据之间的内在关系把样本划分为若干类别,使得同类别样本之间的相似度高,不同类别之间的样本相似度低(即增大类内聚,减少类间距)。
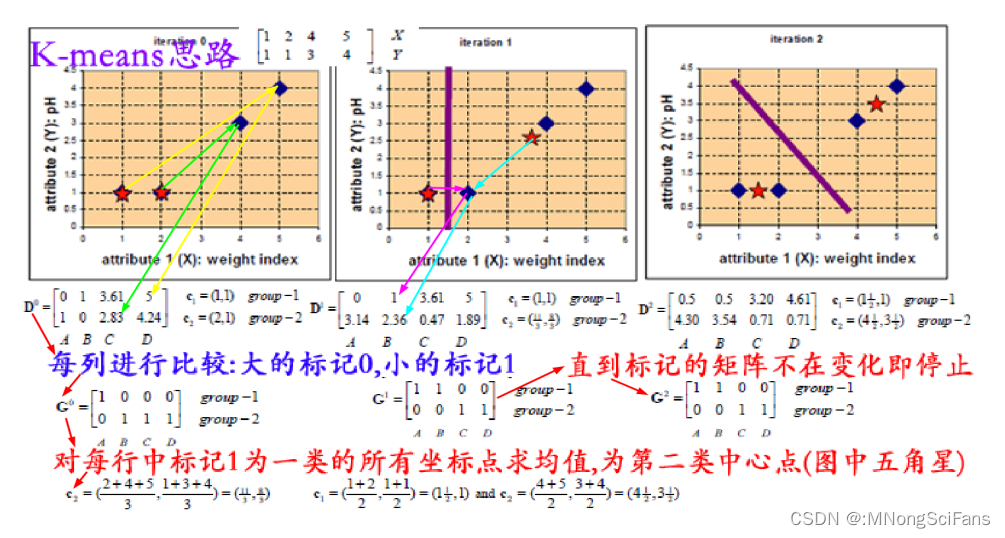
- 首先,我们选择一些类/组,并随机初始化它们各自的中心点。为了算出要使用的类的数量,最好快速查看一下数据,并尝试识别不同的组。中心点是与每个数据点向量长度相同的位置,在上图中是「X」。
- 通过计算数据点与每个组中心之间的距离来对每个点进行分类,然后将该点归类于组中心与其最接近的组中。
- 根据这些分类点,我们利用组中所有向量的均值来重新计算组中心。
- 重复这些步骤来进行一定数量的迭代,或者直到组中心在每次迭代后的变化不大。你也可以选择随机初始化组中心几次,然后选择看起来提供了最佳结果的运行。
K-Means 的优势在于速度快,因为我们真正在做的是计算点和组中心之间的距离:非常少的计算!因此它具有线性复杂度 O(n)。
另一方面,K-Means 有一些缺点。首先,你必须选择有多少组/类。这并不总是仔细的,并且理想情况下,我们希望聚类算法能够帮我们解决分多少类的问题,因为它的目的是从数据中获得一些见解。K-means 也从随机选择的聚类中心开始,所以它可能在不同的算法中产生不同的聚类结果。因此,结果可能不可重复并缺乏一致性。其他聚类方法更加一致。
K-Medians 是与 K-Means 有关的另一个聚类算法,除了不是用均值而是用组的中值向量来重新计算组中心。这种方法对异常值不敏感(因为使用中值),但对于较大的数据集要慢得多,因为在计算中值向量时,每次迭代都需要进行排序。
聚类属于非监督学习,K均值聚类是最基础常用的聚类算法。它的基本思想是,通过迭代寻找K个簇(Cluster)的一种划分方案,使得聚类结果对应的损失函数最小。其中,损失函数可以定义为各个样本距离所属簇中心点的误差平方和:

KMeans的核心目标是将给定的数据集划分成K个簇(K是超参),并给出每个样本数据对应的中心点。具体步骤非常简单,可以分为4步:

模型原理:K-means算法是一种无监督学习算法,用于聚类问题。它将n个点(可以是样本数据点)划分为k个聚类,使得每个点属于最近的均值(聚类中心)对应的聚类。

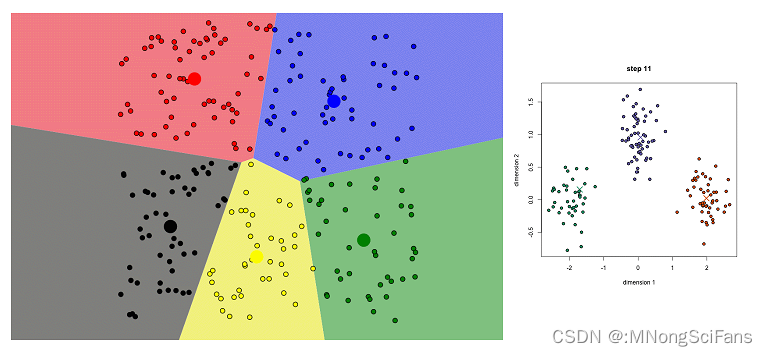
模型训练:通过迭代更新聚类中心和分配每个点到最近的聚类中心来实现聚类。
使用场景:适用于聚类问题,如市场细分、异常值检测等。
对于不同场景,我们的使用聚类的方法也有所不同:
一般场景下的聚类:「变量归一化 --> 分布转换 --> 主成分 --> 聚类」
发现异常境况的聚类:「变量归一化 --> 主成分 --> 聚类」
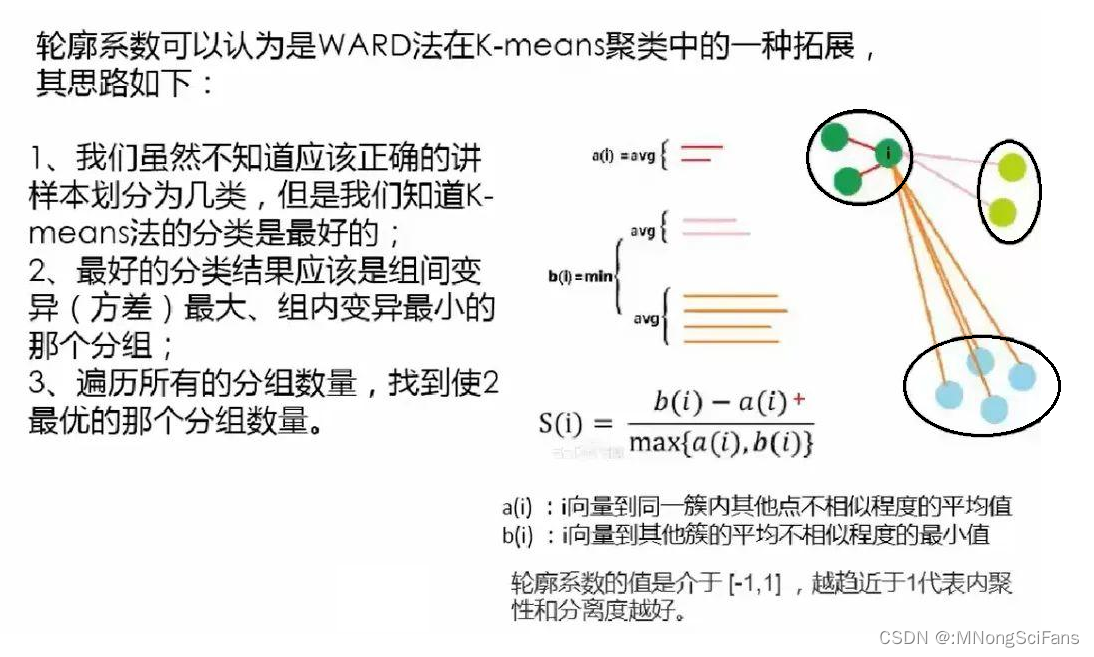
聚类结果好坏不是简单的看统计指标就可得出明确的答案。统计指标是在所有的变量都符合某个假设条件才能表现良好的,而实际建模中很少能达到那种状态;聚类的结果要做详细的描述性统计,甚至作抽样的客户访谈,以了解客户的真实情况,所以让业务人员满足客户管理的目标,是聚类的终极目标。
示例代码(使用Python的Scikit-learn库构建一个简单的K-means聚类器):
# -*- coding: utf-8 -*-
"""
Created on Tue Mar 19 16:50:22 2024
@author: admin
"""
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成模拟数据集
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 创建K-means聚类器对象,K=4
kmeans = KMeans(n_clusters=4)
# 训练模型
kmeans.fit(X)
# 进行预测并获取聚类标签
labels = kmeans.predict(X)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.show()