1. 长度最小的子数组 - 力扣(LeetCode)
1.题目解析:

2.算法原理
(1)方法一:暴力列举出所有的子数组的和
时间复杂度:O(n**2):枚举所有子数组O(n**2)
(2)方法二:
利用单调性(两个指针都不回退),使用"同向双指针"(其实就是滑动窗口)来优化
那么滑动窗口过程是怎么样的?
<1>left = 0,rght = 0
<2>进窗口
<3>判断 并决定什么时候出窗口
(其中二三步是循环的)
还有一步更新结果:这一步可能在<2>,也可能在<3>
以【2,3,1,2,4,3】为例模拟这个过程
开始left和right都指向2(第一个元素),
然后开始进窗口(right++),right指向3,sum从0变为2,
然后进行判断,如果sum>target,更新结果并出窗口(也就是left++);如果sum<=target,继续进窗口(也就是right++)
正确性验证:
利用单调性,规避了很多没有必要的枚举行为(也就是当 sum>target时,right不用继续++)
时间复杂度:O(N)
最坏情况:left和right都走到数组的最后,也就是N+N=2N
3.代码实现
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int sum = 0;
int ret = Integer.MAX_VALUE;
for(int left=0,right=0;right<nums.length;right++) {
sum+=nums[right];//进窗口
while(sum>=target) {//判断
ret = Math.min(right-left+1,ret);//更新结果
sum-=nums[left];
left++;
}
}
//要考虑特殊情况:不存在
return ret==Integer.MAX_VALUE ? 0:ret;
}
}2. 无重复字符的最长子串 - 力扣(LeetCode)
1.题目解析:

2.算法原理
方法一:暴力枚举 + 哈希表(判断字符是否重复出现)
时间复杂度:O(N**2)
方法二:利用规律,使用滑动窗口来解决问题
<1>left = 0,rght = 0
<2>进窗口(right++)—>让字符进入哈希表
<3>判断(窗口内是否出现重复字符)
有重复字符就出窗口(left++),从哈希表中删除该字符,这个过程需要一直重复,直到left找到重复的字符
<4>更新结果:在出完窗口到没有重复字符后就统计结果
3.代码实现
class Solution {
public int lengthOfLongestSubstring(String s) {
char[] ss = s.toCharArray();//字符串转为字符数组
int[] hash = new int[128]; //用数组模拟哈希表
int len = 0;
for(int left=0,right=0;right<s.length();right++) {
//进窗口
hash[ss[right]]++;
while(hash[ss[right]]>1) {//有重复字符
//删除
hash[ss[left]]--;
//出窗口
left++;
}
//更新结果
len = Math.max(len,right-left+1);
}
return len;
}
}3. 最大连续1的个数 III - 力扣(LeetCode)
1.题目解析:
2.算法原理:
问题转化:找出最长的子数组,0的个数不超过k个
方法一:暴力枚举+zero计数器
方法二:在暴力的情况下不让right回退—>滑动窗口
<1>left = 0,rght = 0
<2>进窗口:right++,如果是1,无视;如果是0,计数器+1
<3>判断(zero>k) 并决定什么时候出窗口(left++,计数器-1)
<4>更新结果:出窗口结束
3.代码实现:
class Solution {
public int longestOnes(int[] nums, int k) {
int count=0;
int zero=0;
for(int left=0,right=0;right<nums.length;right++) {
//进窗口
if(nums[right]==0){
zero++;
}
while(zero>k) {//判断:0的个数超过k个
//出窗口
if(nums[left]==0) {
zero--;
}
left++;
}
count=Math.max(count,right-left+1);
}
return count;
}
}1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode)
1.题目解析:

2.算法原理:
正难则反:找出最长的子数组的长度(len),所有元素的和正好等于sum-x(target),那么最后求的就是n-len的最小值
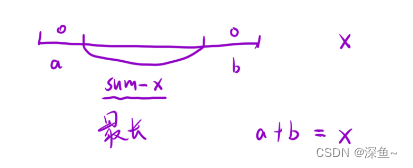
<1>left = 0,rght = 0
<2>进窗口—>Sum+=nums[right]
<3>判断 Sum>target(此处不应该有==,因为要等于不能出窗口)
并决定什么时候出窗口—>sum-=nums[left]
<4>更新结果:这个时候需要加上判断sum==target
3.代码实现:
class Solution {
public int minOperations(int[] nums, int x) {
int Sum=0;
for(int a:nums) Sum+=a;
int sum=0;
int target = Sum-x;
//处理细节
if(target<0) {
return -1;
}
int ret=-1;
for(int left=0,right=0;right<nums.length;right++) {
//进窗口
sum+=nums[right];
//判断
while(sum>target) {
//出窗口
sum-=nums[left++];
}
//更新结果
if(sum==target) {
ret=Math.max(right-left+1,ret);
}
}
return (ret==-1)?(-1):(nums.length-ret);
}
}