算法题如下：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

示例 1：

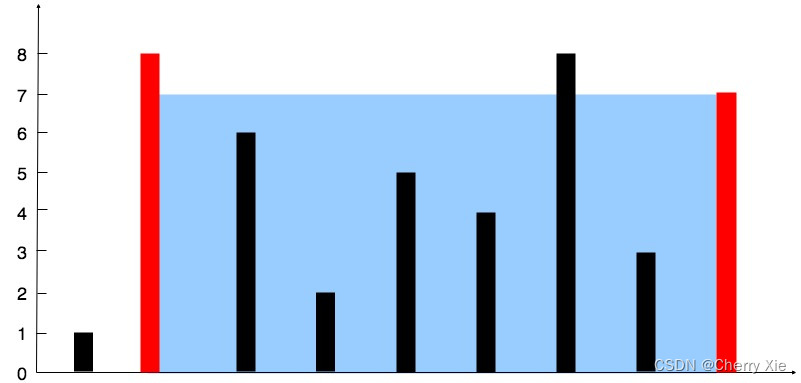
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

无指针解法：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l = len(height)
        max_area = 0
        for i in range(0,l-1):
            for j in range(i,l):
                diff = j-i
                val_y = height[i] if height[i] < height[j] else height[j]
                area = diff * val_y
                max_area = max(max_area,area)
        return max_area

单指针解法：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l = len(height)
        max_area = 0
        diff = 1
        while diff < l:
            for i in range(0,l-diff):
                j = i + diff
                val_l = height[i] if height[i] < height[j] else height [j]
                area = diff * val_l
                if area > max_area:
                    max_area = area
            diff += 1
        return max_area

双指针解法：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        ans = 0
        while l < r:
            area = min(height[l], height[r]) * (r - l)
            ans = max(ans, area)
            if height[l] <= height[r]:
                l += 1
            else:
                r -= 1
        return ans

显然，双指针的解题思路，在时间复杂度上大大优于前两者，量级直接从n^2降到了n。

解题思路

我们都知道。双指针，是一种常见的时间复杂度的优化思路：通过问题的分析数据，将问题转化为，什么情形下左边动，什么情形下右边动的问题。

太晚了，先这样，= =。