Problem: 994. 腐烂的橘子

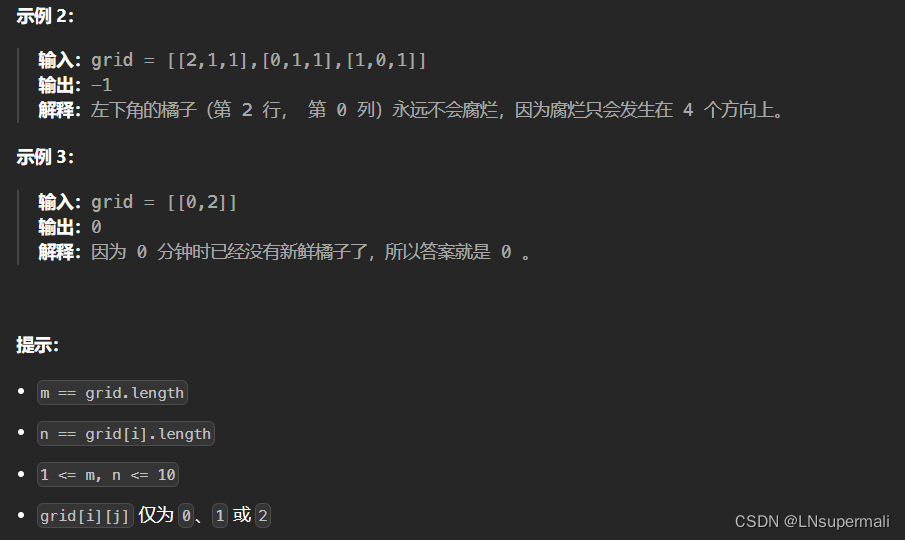
题目描述

思路及解法

1.定义一个二维矩阵dp初始化每个元素值为矩阵的行数乘以列数；用于记录每个新鲜橘子距离第一个腐烂橘子的最早的腐烂时间；
2.遍历矩阵grid若当前橘子是腐烂的橘子，则调用dfs函数；
3.dfs函数实现：void dfs(int depth, vector<vector>& grid, int i, int j);每个参数的意义见代码注释!!!

3.1 若当前索引下标越界或者当前位置没有橘子（grid[i][j] == 0），或者当前橘子距离第一腐烂的橘子的腐烂时间大于或等于其距离第一腐烂的橘子最短腐烂时间（depth >= dp[i][j]）则终止递归；
3.2 每次更新当前的新鲜橘子距离第一个腐烂橘子的最早的腐烂时间；
3.3 dfs当前位置新鲜橘子的上、左、下、右四个方向的橘子；

4.遍历dp数组更新所有橘子腐烂的最短时间（具体操作看代码!!!）

复杂度

时间复杂度:

$O(M\times N)$;其中$M$为矩阵grid的行数，$N$为矩阵grid的列数

空间复杂度:

$O(M\times N)$

Code

class Solution {
    //Minimum storage time
    vector<vector<int>> dp;
public:
    /**
     * Get the minimum orange decay time
     *
     * @param grid A matrix for storing the state of an orange
     * @return int
     */
    int orangesRotting(vector<vector<int>>& grid) {
        int minutes = 0;
        int m = grid.size();
        int n = grid[0].size();
        dp = vector(m, vector<int>(n, m * n));
        int res = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    dfs(0, grid, i, j);
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] != 0) {
                    res = max(dp[i][j], res);
                }
            }
        }
        return res == m * n ? -1 : res;
    }

    /**
     * DFS function implementation
     * 
     * @param depth Record the minimum decay time of the orange in the current location
     * @param grid A matrix for storing the state of an orange
     * @param i Index subscript
     * @param j Index subscript
     */
    void dfs(int depth, vector<vector<int>>& grid, int i, int j) {
        if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] == 0 || depth >= dp[i][j]) {
            return;
        }
        dp[i][j] = min(depth, dp[i][j]);
        dfs(depth + 1, grid, i - 1, j);
        dfs(depth + 1, grid, i, j - 1);
        dfs(depth + 1, grid, i + 1, j);
        dfs(depth + 1, grid, i, j + 1);
        return;
    }
};