前言

进入第 5 章《字符串》的学习，本篇主要内容包括：键索引计数法、低位优先基数排序、高位优先基数排序、三向基数快速排序。

参考目录

• B站 普林斯顿大学《Algorithms》视频课
  （请自行搜索。主要以该视频课顺序来进行笔记整理，课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。）
• 微信读书《算法（第4版）》
  （本文主要内容来自《5.1 字符串排序》）
• 官方网站
  （有书本配套的内容以及代码）

学习笔记

注1：下面引用内容如无注明出处，均是书中摘录。
注2：所有 demo 演示均为视频 PPT demo 截图。
注3：如果 PPT 截图中没有翻译，会在下面进行汉化翻译，因为内容比较多，本文不再一一说明。

1：Java 字符串

字符串： 字符序列。

重要的基本抽象概念。

• 基因组序列：在生物信息学中，基因组序列就是由一系列核苷酸（A、T、C、G）组成的字符串，用于描述 DNA 或 RNA 分子的顺序。
• 信息处理：字符串处理是计算理论和应用的核心部分，涉及文本搜索、替换、格式化、压缩、加密等各种操作。
• 通信系统：例如在电子邮件系统中，邮件正文、主题以及发件人和收件人的地址都是以字符串形式表示和传输的。
• 编程系统：在诸如 Java 等编程语言中，字符串是一种核心数据类型，用来存储和操作任意长度的字符序列。

1.1：字符串数字类型

字符串数据类型（String Data Type）： Java 中不可变字符序列类型。

长度（Length）： 计算字符串中字符的数量。
索引（Indexing）： 使用索引值访问并获取字符串中的特定位置上的字符。
连接（Concatenation）： 将一个字符串与另一个字符串尾部相接合，以生成一个新的合并字符串。

2：键索引计数法 key-indexed counting

2.1：排序算法回顾

下界： 对于基于比较的算法，任何算法都需要大约 NlgN 次比较。

Q. 我们是否能够做得更好（尽管存在这个下界限制）？
A. 是的，前提是不依赖于关键键值的直接比较操作。例如，通过利用数组访问一次性做出 R 路选择（而不是每次比较仅做二选一的决定）。

2.2：关于 key 的假设

假设： 键是介于 0 和 R-1 之间的整数。
推论： 可以使用键作为数组的索引。

应用举例：
• 按首字母对字符串进行排序。
• 按班级分组对名单进行排序。
• 按区号对电话号码进行排序。
• 用作排序算法中的子程序。

注意： 由于键可能与相关的数据项关联，所以不能仅通过计算每个特定键值的数量来进行处理。

2.3：demo 演示

对应书本章节《5.1.1 键索引计数法》：

• 5.1.1.1 频率统计
  • 第一步就是使用 int 数组 count[] 计算每个键出现的频率。
• 5.1.1.2 将频率转换为索引
  • 接下来，我们会使用 count[] 来计算每个键在排序结果中的起始索引位置。
• 5.1.1.3 数据分类
  • 在将 count[] 数组转换为一张索引表之后，将所有元素（学生）移动到一个辅助数组 aux[] 中以进行排序。
• 5.1.1.4 回写
  • 因为我们在将元素移动到辅助数组的过程中完成了排序，所以最后一步就是将排序的结果复制回原数组中。

目标： 对由 0 到 R - 1 之间的 N 个整数组成的数组 a[] 进行排序。

• 使用键（即数组元素本身）作为索引，统计每个整数出现的频率。

• 计算各整数的频次累积值，以确定它们在排序后的新位置（目的地）。

• 利用键（元素值）作为索引访问频次累积数组，根据累积值将原数组中的元素移动到对应的新位置。

过程说明：a[i] 为原始数组， count[r] 为累积数组，aux[i] 为临时新数组。

依次遍历原始数组，找到累积数组中对应 key 的值作为临时新数组的下标存进去。如：

• 已知：a[0] = d，count[d] = 6
• 可得：aux[6] = d
• 更新：count[d] = 6 + 1 = 7

得到最终结果如下：

最终步骤：

• 将排序后的元素复制回原始数组 a[] 中。

2.4：分析

命题： 键索引排序所需时间与 N+R 成正比。
命题： 键索引计数法所需的额外存储空间与 N+R 成正比。
稳定？ √

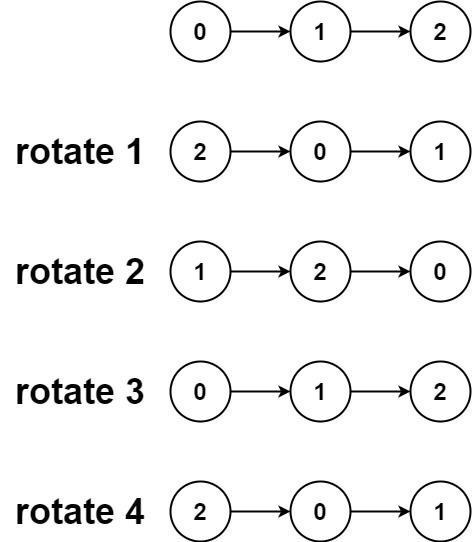
3：低位优先基数排序 LSD radix sort

3.1：介绍

低位优先的字符串 (基数) 排序 Least-significant-digit-first (LSD) string (radix) sort

LSD 字符串（基数）排序。

• 从右向左考虑字符。
• 使用第 d 个字符作为键（采用键索引计数法）进行稳定排序。

3.2：证明

命题： LSD 排序算法能确保将固定长度的字符串按升序排列。

证明： （通过归纳法对 i 进行证明）
在完成第 i 轮排序后，所有字符串都会依据其最后 i 个字符进行有序排列。

• 如果两字符串在当前所使用的排序键上不一致，则键索引排序将会把它们按照正确的相对顺序排列好。
• 如果两字符串在当前排序键上相等，则由于排序算法的稳定性，它们原有的相对顺序会被维持不变。

命题： LSD 排序算法具有稳定性。
证明： 由于键索引计数法具有稳定性，所以 LSD 排序也是稳定的。

3.3：Java 实现

edu.princeton.cs.algs4.LSD

edu.princeton.cs.algs4.LSD#sort

3.4：排序算法小结

4：高位优先基数排序 MSD radix sort

4.1：介绍

高位优先的字符串 (基数) 排序 Most-significant-digit-first (MSD) string (radix) sort

4.2：示例

对于可变长度字符：

将字符串视为在其末尾附加了一个额外的字符（该字符小于任何其他字符）。

C语言字符串： 末尾自动带有额外的字符 '\0'，因此无需做额外工作。

4.3：Java 实现

edu.princeton.cs.algs4.MSD

edu.princeton.cs.algs4.MSD#sort

4.4：潜在风险

观察1： 对于较小的子数组，该算法极其缓慢。

• 每次函数调用都需要自己的 count[] 数组。
• 对于 ASCII 字符集（256 个计数）：当 N 等于 2 时，其速度比单纯的复制操作慢大约 100倍。
• 对于 Unicode 字符集（65536 个计数）：当 N 等于 2 时，其速度比单纯的复制操作慢大约 32000 倍。

观察2： 由于递归的原因，会产生大量极小的子数组。

解决方案： 针对较小的子数组设置一个阈值转为插入排序。

• 使用插入排序法，不过是从字符串的第 d 个字符处开始进行排序操作。
• 实现自定义的 less() 比较函数，确保其在比较时从字符串的第 d 个字符开始。

4.5：性能

所检查字符的数量：

• MSD 只会检查刚好足够对键进行排序所需的字符数。
• 所需检查的字符数量依赖于具体的键值。
• 在输入数据量上，检查字符的数量可能会呈现亚线性的时间复杂度特性（基于compareTo() 方法的排序同样也可能具有亚线性时间复杂度特性！）

4.6：排序算法小结

5：三向基数快速排序 3-way radix quicksort

5.1：介绍

三向字符串快速排序 3-way string quicksort

概述： 在第 d 个字符上执行三向分区操作。

• 相较于 MSD 字符串排序法中的多路划分，此方法所需额外处理较少。
• 不会再次检查与分区字符相同的字符（然而对于不等于分区字符的字符仍会进行重新检查）。

书中的相关描述：

5.2：Java 实现

edu.princeton.cs.algs4.Quick3string

edu.princeton.cs.algs4.Quick3string#sort

5.3：排序算法小结

对应书本的表格：