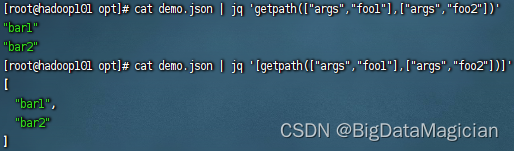
文章目录
- 探索多视角驱动的层次内容感知网络用于指静脉识别
- 总结
- 摘要
- 介绍
- 相关工作
- 多视角方法
- 长短时记忆
- 基于视角的目标表达
- 方法
- 全局主干网络
- 局部感知模块
- 损失函数
- 实验和分析
- 数据库
- 实验设置和训练策略
- 消融实验
- 视角一致性的效果
- 参考文献
论文: Exploiting Multiperspective Driven Hierarchical Content-Aware Network for Finger Vein Verification
探索多视角驱动的层次内容感知网络用于指静脉识别
总结
这是一个基于深度学习的指静脉识别方法。从任务类型上来说是分类任务。具体来说是多视角方法。
把问题分解为特征提取和最后的分类映射,而单纯的2D特征显然不够充分,受到很多因素影响,因此研究多视角3D特征学习是有意义的。
中心思想依然是围绕特征,作者将特征分为局部和全局特征,形成层次。因为有研究表明,加入局部特征可以使最后的特征分辨力更强。全局特征使用循环神经网络一个双向CNN-GRU提取,将输入的不同视角的图片作为按一定顺序的图像序列进行处理,为了避免视角顺序的影响,所以使用了双向网络,分为前向后向。同时为了更好的保存信息,使用了一种记忆加权策略,和最终隐状态相似度越高,说明中间状态贡献越大,因此权重越高。而对于局部特征的提取,使用了信息熵引导的空间变换网络,图像熵能够说明一个区域内灰度的变化程度,反映出这个区域特征的可分性,图像熵越大,说明信息越丰富空间变换网络可以学习仿射参数截取感兴趣的区域,一个问题是图像熵最大化目标不可微,为了解决这个问题,选择使用两个通路,即如果把图像熵的计算串联放到网络中去,无法进行训练,因此选择将信息熵作为输入,在网络外进行计算,和原始特征共用仿射参数,以进行训练。当把同一次采集的不同视角图片作为一个序列时,就有了相比于不同采集图片间更好的视角一致性,实验表明效果更好。
摘要
单视角的内容只有很少的指静脉空间网络结构,尽管一根手指的角度有微小的不同依然展示出明显的区别,这些都影响验证表现。因此,这篇工作考虑了不同视角的指静脉图像。我们首先设计了一个低成本的基于多视角的指纹静脉成像装置用于数据搜集。一个名为HCAN的层次内容感知网络(HCAN)被提出用于提取有判别力的层次特征,HCAN由一个全局主干网络(GSN)和一个局部感知模块(LPM)组成。GSN用来从全视角中提取隐3D特征通过一个循环神经网络。它使模型能够保存前一个隐状态的细节结合一个记忆加权策略。LPM被设计用来从图像熵的角度感知每个视角。由熵损失引导,LPM捕捉局部的主带特征并提升层次特征的分辨性和鲁棒性。
介绍
因为指静脉是一个内在特征,体素和点云无法通过现成的方法直接采集。一个替代方法使围绕手指径向采集固定角度间隔的多个视角的指静脉图片。特别地,由轻量卷积神经网络和一个是双向门控循环单元(ConvBiGRU)组成的全局主干神经网络(ConvBiGRU),被用来捕捉隐全局3D特征和多视角间的相关信息。对于局部特征提取和增强,我们设计了一个局部感知模块(LPM)和一个新颖的熵函数。它可以注意到每个视角的高对比度包含清晰血管区域的主要位置,让特征更加具有可分性。
我们的主要贡献总结如下:
- 一个低成本多视角成像设备
- 一个用于多视角指静脉识别的深度神经网络
- 一个引入GSN的记忆加权策略
- 一个用来获取局部特征的局部感知模块(LPM)
相关工作
多视角方法
因为单视角图像缺乏3D指静脉结构信息,在提升特征可分性熵陷入瓶颈。但是,基于多视角指静脉识别的研究依然稀缺。参考31基于立体匹配技术从几乎一侧的三个视角中生成手指静脉的点云。最近32的工作提出一整个验证系统,包含硬件和软件。3D指静脉首先通过全视角的指静脉重建然后通过设计的CNN提取用来验证。
因为单视角图像缺乏3D信息,我们的HCAN使用多视角指静脉图像作为输入来探索层次特征通过3D隐特征和主导局部特征。除此之外,HCAN也考虑了指静脉的特点并且应用LPM结合图像熵损失来感知每个视角来确定包含清晰高对比度血管区域。
长短时记忆
提出的HCAN结合了LSTM来分析不同指静脉视角的关系。提出一个记忆加权策略来从最终表达中保留更多的隐状态信息。
基于视角的目标表达
41嵌入一个无向图模型到方法中来联合学习空间信息和视觉信息。Ma42应用了一个标准LSTM来聚合视角特征和捕捉输入序列的依赖。最近,图神经网络备用与捕捉不同视角间的关系。huang10通过解纠缠类相关特征和视图排列相关来表示多视图对象特征。xu44提出里相关感知表达模块来提取视角间和视角内特征。类似地,多层次视角联合卷积网络(MLVACN)是一个统一的端到端框架旨在获取不同视角间的关系。不像上述的方法,HCAN从两个分支中通过学习隐全局3D特征和主导局部特征来一曲多视角指静脉层次特征。(即GSN和LPM),是第一个考虑多视角指静脉验证方法。我们通过LPM有效提取了视角特定的特征(即主导局部特征)来丰富最后的表达通过一个新颖的视觉熵损失。除此之外,结合一个记忆加权的策略来避免遗忘掉其他视角的细节。
方法
在这个部分,我们展示了我们方法的细节。我们网络的整体如图三所示。由两个组件组成,称为GSN和LPM。我们应用GSN来把所有的视角压缩为一个包含3D信息和视角间隐关系的全局特征嵌入。一个完全可微模块LPM引入以使得特征更加可分。图像熵隶属于可学习的LPM模块在视角图像中确定主导任意大小包含可分辨信息的主导区域并增强主导局部特征。全军和局部特征都用来组成可分辨的层次特征,用来进行指静脉分割。

全局主干网络
一个人不同视角的指静脉可以被看作一个图像序列
V
=
v
i
i
=
1
N
V = {v_i}_{i=1}^{N}
V=vii=1N,在我们的情况下,
N
=
3
N=3
N=3为视角数目。每个视角的特征映射
m
i
m_i
mi可以被一个非线性函数
F
\mathcal{F}
F提取。
m
i
=
F
(
v
i
)
m_i = \mathcal{F}(v_i)
mi=F(vi)
我们使用一个浅但是有效网络通过堆叠多个inception块来达到模型大小和表现的平衡。考虑到网络深度和尺寸,我们以处理1x1卷积,被应用来压缩通道维度。除此之外,使用多个不同核尺寸的分支来发掘静脉特征是有用的因为手指的静脉宽度是多样的,所有分支的输出结合起来作为整个块的输出。

在我们的网络中,所有的卷积层后跟一BN层,输出又ReLU激活。卷积步长设置为1。
接下来,一个输入视角序列 V V V的提取特征映射组成了一个特征序列 M = { m i } i = 1 N M=\{m_i\}_{i=1}^N M={mi}i=1N我们组合所有 M M M来探索他们间隐全局3D特征和相关信息。不同于使用视角池化操作,在这里采用一个卷积GRU(ConvGRU),包含两种门:重置门
和更新门。
给定特征序列
M
∈
R
B
×
N
×
C
×
H
×
W
M \in {\mathbb{R}^{B\times N\times C \times H\times W}}
M∈RB×N×C×H×WConvGRU单元的前向过程表达如下:
r
t
=
σ
(
W
r
∗
[
h
t
−
1
;
m
t
]
)
u
t
=
σ
(
W
u
∗
[
h
t
−
1
;
m
t
]
)
h
′
=
t
a
n
h
(
W
∗
[
r
t
∗
h
t
−
1
;
m
t
]
)
h
t
=
(
1
−
u
t
)
∗
h
t
−
1
+
u
t
∗
h
′
r_t = \sigma(W_r\ast [h_{t-1};m_t])\\ u_t = \sigma(W_u \ast [h_{t-1};m_t])\\ h^{'} = tanh(W *[r_t\ast h_{t-1};m_t])\\ h_t = (1 - u_t) \ast h_{t-1}+u_t \ast h^{'}
rt=σ(Wr∗[ht−1;mt])ut=σ(Wu∗[ht−1;mt])h′=tanh(W∗[rt∗ht−1;mt])ht=(1−ut)∗ht−1+ut∗h′
∗
\ast
∗是卷积操作,
r
,
u
r,u
r,u表示重置门和更新门,
;
;
;表示特征拼接。重置门
r
t
r_t
rt决定之前隐藏状态的哪些信息应该和当前输入
m
t
m_t
mt结合。而更新门决定之前隐藏状态的信息保留。视图顺序t处的隐藏状态包含关于序列中前t个视图的“记忆”。为了避免视角顺序的干预和更好的效果,我们最终使用了ConvBiGRU将前向和后向序列都作为输入。在我们的工作,前向视角序列顺序是从左到右,后向相反。
直觉上来说,最后的隐藏状态
h
N
h_N
hN可以直接用作序列处理的全局特征。尽管之前的记忆可能有一些有用的细节,但是它带来了冗余信息。为了保存更多记忆中的细节,我们提出里一个记忆加权策略来通过记忆相似度决定最后的输出。具体来收,所有的隐状态根据和最后隐状态
h
n
h_n
hn的相似度来表示贡献,通过下式计算。
h
=
∑
i
N
a
i
H
i
h = \sum_i^{N}{a_iH_i}
h=i∑NaiHi
a i = 0.5 + 0.5 × M S ( i , N ) a_i = 0.5 + 0.5 \times MS(i, N) ai=0.5+0.5×MS(i,N)
给定两个"记忆"(即隐状态)
h
i
,
h
j
∈
R
C
×
H
×
W
h_i, h_j \in R^{C \times H \times W}
hi,hj∈RC×H×W在第$i, j
个时间步,相似度
个时间步,相似度
个时间步,相似度MS(i, j)$定义为
M
S
(
i
,
j
)
=
1
H
W
∑
m
=
1
H
∑
n
=
1
W
h
i
(
m
,
n
)
h
j
(
m
,
n
)
∥
h
i
(
m
,
n
)
∥
2
∥
h
j
(
m
,
n
)
∥
2
,
MS(i,j)=\frac{1}{HW}\sum_{m=1}^{H}\sum_{n=1}^{W}\frac{\mathbf{h}_{i}^{(m,n)}\mathbf{h}_{j}^{(m,n)}}{\|\mathbf{h}_{i}^{(m,n)}\|_{2}\|\mathbf{h}_{j}^{(m,n)}\|_{2}},
MS(i,j)=HW1m=1∑Hn=1∑W∥hi(m,n)∥2∥hj(m,n)∥2hi(m,n)hj(m,n),
表示在第i个隐藏状态
h
i
(
m
,
n
)
h_i^{(m,n)}
hi(m,n)中沿着通道维度的坐标(m,n)处的矢量。
最后我们将投票后的隐状态组合成一个向量并将其送入一个全连接层来得到最后的隐全局3D特征。
局部感知模块
我们使用LPM来提取有分辨能力的局部特征,给定一张指静脉图片,给出特定信息的部分经常会吸引我们眼球,除此之外,这些区域可以被用来区分两张图片。我们称之为主导特征。
1)区域定位器:为了发现和定位这些主导特征,这个模块应当由两种能力。一方面,它需要感知图片或者相应的特征来决定哪个区域或者特征是主导的。零一方面,它可以切分区域或者定位它们。因此,我们引入空间变换网络(STN)到LPM中去感知整个输入来定位图像中的主导区域并提取主导特征。它有三个优势(1)完全可微(2)可以放入网络任何位置二步显著增加计算(3)可以通过一个仿射变换学习截取一个感兴趣区域。这些因素使得STN非常适合感知输入内容。

由定位网络
θ
p
i
\theta _{pi}
θpi,一个网格生成器和一个采样器组成。定位网络用于学习仿射参数
Θ
\Theta
Θ。之后栅格坐标通过网格坐标器根据仿射参数生成。在我们的工作中,仿射变换可以写为:
(
x
i
i
n
y
i
i
n
1
)
=
Θ
(
x
i
o
u
t
y
i
o
u
t
1
)
=
[
a
b
c
d
e
f
]
(
x
i
o
u
t
y
i
o
u
t
1
)
\begin{pmatrix}x_i^{in}\\y_i^{in}\\1\end{pmatrix}=\Theta\begin{pmatrix}x_i^{out}\\y_i^{out}\\1\end{pmatrix}=\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}\begin{pmatrix}x_i^{out}\\y_i^{out}\\1\end{pmatrix}
xiinyiin1
=Θ
xioutyiout1
=[adbecf]
xioutyiout1
Θ
=
[
a
b
c
d
e
f
]
\Theta = \begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}
Θ=[adbecf]是定位网络的输出。
(
x
i
n
,
y
i
n
)
(x_{in}, y_{in})
(xin,yin)和
(
x
o
u
t
,
y
o
u
t
)
(x_{out}, y_{out})
(xout,yout)是输入图像和输出图像规则网格的坐标。每个视角的主导区域通过一个独立地STN从输入视角中学习。除此之外,学习4个仿射参数
[
a
,
e
,
c
,
f
]
[a, e, c, f]
[a,e,c,f]。为了保留区域的信息,避免退化,我们固定b = d = 0。对于定位网络,它将特征图
m
i
m_i
mi作为u输入。之后我们沿着通道维度通过两个卷积层压缩特征图
m
i
m_i
mi,步长和卷积核尺寸均为1,卷积核数分别为32和8。最后,仿射参数通过一个4维输出的全连接层获取。之后,主导区域可以通过基于仿射参数的网格生成器截取。输出区域为16 x 16。
因为全局特征通过GSN捕捉,我们拼接每个视角的主导区域并且通过一些卷积层提取聚合特征 f l o c a l ∈ R 128 f_{local}\in \mathbb{R}^{128} flocal∈R128。最后,拼接主导局部特征 f l o c a l f_{local} flocal和全局特征 f g l o b a l f_{global} fglobal作为最后的层次特征 f ∈ R 256 f\in{\mathbb{R}^{256}} f∈R256用来验证。
2)使用图像熵来感知
经验上,更高对比度和更清晰内容的区域更吸引我们的注意力,但是指静脉图像中的区域并不总是主导的,使得特征的可分性减少。除此之外,STN尽力定位理想的主导区域如果损失函数在最终纠缠特征或者表达上应用。我们引入图像熵来直接感知输入图像。可以被表达为:
H
(
I
)
=
−
∑
k
=
0
N
−
1
p
k
l
o
g
2
p
k
H(I) = -\sum_{k = 0}^{N-1}p_klog_2p_k
H(I)=−k=0∑N−1pklog2pk
N
N
N表示灰度级的数目,
p
k
p_k
pk表示这些像素有灰度
k
k
k的概率,当概率相等时,熵最大。对于一个指静脉图片的不清晰区域灰度值通常变化较慢,分布比较集中,因此相应的熵较小。因此LPM损失函数可以写成下面形式。
(
x
l
^
,
y
l
^
)
,
(
x
r
^
,
y
r
^
)
=
arg
max
(
x
l
,
y
l
)
,
(
x
r
,
y
r
)
H
(
r
e
g
i
o
n
(
x
r
,
y
r
)
(
x
l
,
y
l
)
)
,
s.t.
c
o
l
(
I
)
>
x
r
>
x
l
>
0
,
r
o
w
(
I
)
>
y
l
>
y
r
>
0
\begin{aligned}(\hat{x_l},\hat{y_l}),(\hat{x_r},\hat{y_r})&=\arg\max_{(x_l,y_l),(x_r,y_r)}H(region_{(x_r,y_r)}^{(x_l,y_l)}),\\\text{s.t.}col(\mathbf{I})&>x_r>x_l>0,\\row(\mathbf{I})&>y_l>y_r>0\end{aligned}
(xl^,yl^),(xr^,yr^)s.t.col(I)row(I)=arg(xl,yl),(xr,yr)maxH(region(xr,yr)(xl,yl)),>xr>xl>0,>yl>yr>0
但是这个损失函数不可微,是一个严重的问题。为了解决这个问题,我们提出里使用双数据路径分享相同的仿射函数来表达一张图片的两种信息。一条通路接受原始的图像数据,另一条允许熵数据流动。具体来说,在熵数据通路,区域熵矩阵首先被计算出,并和相应的图像输入按对应的通路输入模型中。

计算图像熵的方式如上图所示。最后的区域上矩阵计算如下
E
n
t
(
x
,
y
)
r
=
−
∑
k
=
0
N
−
1
p
k
log
2
p
k
Ent_{(x,y)}^r=-\sum_{k=0}^{N-1}p_k\log_2p_k
Ent(x,y)r=−k=0∑N−1pklog2pk
最后的区域损失
L
e
n
t
=
−
∥
G
E
p
∥
T
\mathcal{L}_{ent} = -\Vert GE_p\Vert^T
Lent=−∥GEp∥T
G
G
G是加权矩阵

损失函数
在我们的工作中,我们选择了circle损失,被证明可以有效得到特征表达。
L
c
i
r
c
l
e
=
log
[
1
+
∑
j
=
1
L
exp
(
γ
α
n
j
(
s
n
j
−
Δ
n
)
)
∑
i
=
1
K
exp
(
−
γ
α
p
i
(
s
p
i
−
Δ
p
)
)
]
\begin{aligned}&\mathcal{L}_{circle}\\&=\log[1+\sum_{j=1}^{L}\exp(\gamma\alpha_{n}^{j}(s_{n}^{j}-\Delta_{n}))\sum_{i=1}^{K}\exp(-\gamma\alpha_{p}^{i}(s_{p}^{i}-\Delta_{p}))]\end{aligned}
Lcircle=log[1+j=1∑Lexp(γαnj(snj−Δn))i=1∑Kexp(−γαpi(spi−Δp))]
两个模块的损失函数的加权和是最后的损失函数
L
=
L
G
S
N
+
L
L
P
M
=
L
c
i
r
c
l
e
1
+
λ
1
L
c
i
r
c
l
e
1
+
λ
2
L
e
n
t
\begin{aligned} \mathcal{L} &= \mathcal{L}_{GSN}+\mathcal{L}_{LPM} \\&= \mathcal{L}_{circle_1}+\lambda_1\mathcal{L}_{circle_1}+\lambda_2 \mathcal{L}_{ent} \end{aligned}
L=LGSN+LLPM=Lcircle1+λ1Lcircle1+λ2Lent
实验和分析
数据库
1)THU-MFV
2)LMVFV
实验设置和训练策略
所有图像首先进行直方图归一化然后Resize到64x63。因为联合训练CNN和GRU比较困难,因此,在一阶段,先训练CNN。训练前的数据增强如下:
- 平移
- 改变对比度
- 高斯模糊
消融实验


视角一致性的效果
再一次获取中,一根手指的不同视角间存在一些相关性或者隐含关系。我们称这些相关性视角一致性。在视角一致性约束下,输入图像被打包成一个图片序列V。即一次采集中的图像组合成一个序列。为了让解释视角一致性的作用,实验结果如表七所示。显示了一次采集中不同视角间的关系和相关性可以提供更多可分辨信息。

参考文献
【31】S. Bunda, “3D point cloud reconstruction based on the finger vascular pattern,” B.S. thesis, Dept. Elect. Eng., Univ. Twente, Enschede, The Netherlands, 2018
【32】W. Kang, H. Liu, W. Luo, and F. Deng, “Study of a full-view 3D finger vein verification technique,” IEEE Trans. Inf. Forensics Security, vol. 15, pp. 1175–1189, 2020.
【41】A. Liu, W. Nie, and Y. Su, “3D object retrieval based on multi-view latent variable model,” IEEE Trans. Circuits Syst. Video Technol., vol. 29, no. 3, pp. 868–880, Mar. 2019.
【42】C. Ma, Y. Guo, J. Yang, and W. An, “Learning multi-view representation with LSTM for 3-D shape recognition and retrieval,” IEEE Trans. Multimedia, vol. 21, no. 5, pp. 1169–1182, Oct. 2019.
【44】Y. Xu, C. Zheng, R. Xu, Y. Quan, and H. Ling, “Multi-view 3D shape recognition via correspondence-aware deep learning,” IEEE Trans. Image Process., vol. 30, pp. 5299–5312, 2021.