机器学习----交叉熵(Cross Entropy)如何做损失函数

一.概念引入

1.损失函数

2.均值平方差损失函数

3.交叉熵损失函数

3.1信息量

3.2信息熵

3.3相对熵

二.交叉熵损失函数的原理及推导过程

表达式

二分类

联立

取对数

补充

三.交叉熵函数的代码实现

一.概念引入

1.损失函数

损失函数是指一种将一个事件（在一个样本空间中的一个元素）映射到一个表达与其事件相关的经济成本或机会成本的实数上的一种函数。在机器学习中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。

不同的任务类型需要不同的损失函数，例如在回归问题中常用均方误差作为损失函数，分类问题中常用交叉熵作为损失函数。

2.均值平方差损失函数

定义如下： $L(y,f(x;\Theta )) = \frac{1}{N}\sum_{i = 1}^{N}(yi - f(xi;\Theta ))^{2}$

意义：N为样本数量。公式表示为每一个真实值与预测值相减的平方去平均值。均值平方差的值越小，表明模型越好。

对于回归问题，均方差的损失函数的导数是局部单调的，可以找到最优解。但是对于分类问题，损失函数可能是坑坑洼洼的，很难找到最优解。故均方差损失函数适用于回归问题。

3.交叉熵损失函数

交叉熵是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性。在机器学习中，交叉熵表示真实概率分布与预测概率分布之间的差异。其值越小，模型预测效果就越好。

交叉熵损失函数的公式为：
$L = -(y log \hat{y} +(1-y)log(1- \hat{y}))$

其中，y表示样本的真实标签，\hat{y}表示模型预测的标签。当y=1时，表示样本属于正类；当y=0时，表示样本属于负类。

3.1信息量

信息量是指信息多少的量度。

比如说

1：太阳从东边升起，这个信息量就是0，因为这个是一句废话。没有不确定性的东西。
2：今天会下雨。从直觉上来看，这个信息量就比较大了，因为今天天气具有不确定性，但是这句话消除了不确定性。

根据上述总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量就越小，概率越小，信息量就越大。设某件事发生的概率为p(xi),则信息量为：

$I(xj) = -ln(p(xi))$

3.2信息熵

信息熵是信息论中的一个重要概念，用于衡量一个系统或信号中信息量的不确定性或随机性。

信息熵的定义可以用数学公式表示。假设有一个离散的随机变量X，它可以取n个不同的可能值 $x_1,x_2,\ldots,x_n$ ，每个可能值的概率为 $p_1,p_2,\ldots,p_n$ ，则信息熵H(X)的计算公式为：

$H(X)=-\sum_{i=1}^{n}p_i\log_2p_i$

其中， $\log_2$ 表示以2为底的对数。

信息熵的物理意义是：它表示了在给定概率分布的情况下，系统的平均不确定性或信息量。信息熵的值越大，表示系统的不确定性越高；信息熵的值越小，表示系统的不确定性越低。

3.3相对熵

相对熵，也称为KL 散度（Kullback-Leibler Divergence），是一种用于比较两个概率分布差异的度量。它衡量了一个概率分布P与另一个参考概率分布Q之间的差异程度。

相对熵的定义为：

$D_{KL}(P||Q)=\sum_{x}P(x)\log\frac{P(x)}{Q(x)}$

其中，P(x)和Q(x)分别是概率分布P和Q在事件x上的概率。

相对熵的物理意义是：它表示了将概率分布P表示为参考概率分布Q的编码时所需的额外信息量。如果P和Q非常接近，相对熵的值会比较小；如果P和Q差异较大，相对熵的值会比较大。
KL散度=交叉熵-信息熵
相对熵在机器学习、信息论和统计学中有广泛的应用。它可以用于评估两个模型或概率分布的相似性，比较数据分布的差异，以及在熵最小化的框架下进行优化等。

例如，在机器学习中，相对熵常用于比较真实数据的分布和模型预测的分布之间的差异，以评估模型的性能。较小的相对熵值表示模型预测的分布与真实分布更接近。

二.分类问题中的交叉熵

1.二分类问题中的交叉熵

把二分类的交叉熵公式 4 分解开两种情况：

当 y=1 时，即标签值是 1 ，是个正例，加号后面的项为: $loss=-log(a)$
当 y=0 时，即标签值是 0 ，是个反例，加号前面的项为 0 : $loss=-log(1-a)$

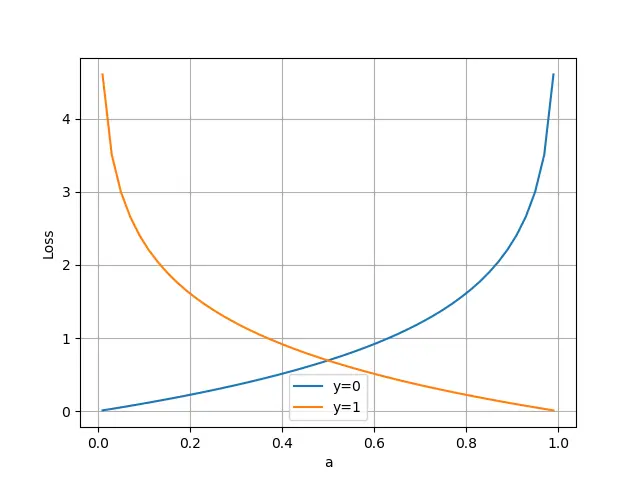
横坐标是预测输出，纵坐标是损失函数值。 y=1 意味着当前样本标签值是1，当预测输出越接近1时，损失函数值越小，训练结果越准确。当预测输出越接近0时，损失函数值越大，训练结果越糟糕。此时，损失函数值如下图所示。

2.多分类问题中的交叉熵

假设希望根据图片动物的轮廓、颜色等特征，来预测动物的类别，有三种可预测类别：猫、狗、猪。假设我们训练了两个分类模型，其预测结果如下:

模型1:

预测值标签值是否正确
0.3 0.3 0.4 0 0 1（猪）正确
0.3 0.4 0.4 0 1 0（狗）正确
0.1 0.2 0.7 1 0 0（猫）错误

每行表示不同样本的预测情况，公共 3 个样本。可以看出，模型 1 对于样本 1 和样本 2 以非常微弱的优势判断正确，对于样本 3 的判断则彻底错误。

模型2:

预测值标签值是否正确
0.1 0.2 0.7 0 0 1（猪）正确
0.1 0.7 0.2 0 1 0（狗）正确
0.3 0.4 0.4 1 0 0（猫）错误

可以看出，模型 2 对于样本 1 和样本 2 判断非常准确（预测概率值更趋近于 1），对于样本 3 虽然判断错误，但是相对来说没有错得太离谱（预测概率值远小于 1）。

结合多分类的交叉熵损失函数公式可得，模型 1 的交叉熵为:

sample 1 loss = -(0 * log(0.3) + 0 * log(0.3) + 1 * log(0.4)) = 0.91

sample 1 loss = -(0 * log(0.3) + 1 * log(0.4) + 0 * log(0.4)) = 0.91

sample 1 loss = -(1 * log(0.1) + 0 * log(0.2) + 0 * log(0.7)) = 2.30

对所有样本的 loss 求平均:

$L=\frac{0.91+0.91+2.3}{3}=1.37$

模型 2 的交叉熵为:

sample 1 loss = -(0 * log(0.1) + 0 * log(0.2) + 1 * log(0.7)) = 0.35

sample 1 loss = -(0 * log(0.1) + 1 * log(0.7) + 0 * log(0.2)) = 0.35

sample 1 loss = -(1 * log(0.3) + 0 * log(0.4) + 0 * log(0.4)) = 1.20

对所有样本的 loss 求平均:

$L=\frac{0.35+0.35+1.2}{3}=0.63$

可以看到，0.63 比 1.37 的损失值小很多，这说明预测值越接近真实标签值，即交叉熵损失函数可以较好的捕捉到模型 1 和模型 2 预测效果的差异。交叉熵损失函数值越小，反向传播的力度越小。

参考文章-损失函数｜交叉熵损失函数。

预测值	标签值	是否正确
0.3 0.3 0.4	0 0 1（猪）	正确
0.3 0.4 0.4	0 1 0（狗）	正确
0.1 0.2 0.7	1 0 0（猫）	错误

预测值	标签值	是否正确
0.1 0.2 0.7	0 0 1（猪）	正确
0.1 0.7 0.2	0 1 0（狗）	正确
0.3 0.4 0.4	1 0 0（猫）	错误

三.交叉熵损失函数的原理及推导过程

表达式

输出标签表示为10,1}时，损失函数表达式为: $L = -(y log \hat{y} +(1-y)log(1- \hat{y}))$

二分类

二分类问题，假设 $y\epsilon (0,1)$
正例: $P(y = 1 |x) = \hat{y}$ 公式1

反例: $P(y = 0|x) = 1-\hat{y}$ 公式2

联立

将上述两式连乘。
$P(y | x) = \hat{y}^{y}*(1-\hat{y})^{1-y}$ ; 其中 $y\epsilon (0,1)$ 公式3

当y=1时，公式3和公式1一样。
当y=0时，公式3和公式2一样。

取对数

取对数，方便运算，也不会改变函数的单调性。

$logp(y|x) = ylog\hat{y}+(1-y)log(1-\hat{y})$ 公式4
我们希望 $P(y|x)$ 越大越好，即让负值 $-logP(y|x)$ 越小越好，

得到损失函数为 $L = -(y log \hat{y} +(1-y)log(1- \hat{y}))$ 公式5

补充

上面说的都是一个样本的时候，多个样本的表达式是:多个样本的概率即联合概率，等于每个的乘积。

$p(y |x) = \prod_{i}^{m}p(y^{(i)}|x^{(i)})$
$logp(y|x)= \sum_{i}^{m}logp(y^{(i)}x^{(i)})$
由公式4和公式5得到
$logp(y^{(i)} |x^{(i)})=-L(y^{(i)}|x^{(i)})$

$logp(y^{(i)}|x^{(i)})=-\sum_{i}^{m}L(y^{(i)}|x^{(i)})$
加上 $\frac{1}{m}$ 对式子进行缩放。便于计算。
$Cost(min):J(w,b) = \frac{1}{m}\sum_{i}^{m}L(y^{(i)}|x^{(i)})$
或者写作

$J=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})]$

四.交叉熵函数的代码实现

在Python中，可以使用NumPy库或深度学习框架（如TensorFlow、PyTorch）来计算交叉熵损失函数。以下是使用NumPy计算二分类和多分类交叉熵损失函数的示例代码：
import numpy as np

# 二分类交叉熵损失函数
def binary_cross_entropy_loss(y_true, y_pred):
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

# 多分类交叉熵损失函数
def categorical_cross_entropy_loss(y_true, y_pred):
    num_classes = y_true.shape[1]
    return -np.mean(np.sum(y_true * np.log(y_pred + 1e-9), axis=1))

# 示例用法
# 二分类
y_true_binary = np.array([[0], [1], [1], [0]])
y_pred_binary = np.array([[0.1], [0.9], [0.8], [0.4]])
loss_binary = binary_cross_entropy_loss(y_true_binary, y_pred_binary)
print("Binary Cross-Entropy Loss:", loss_binary)

# 多分类
y_true_categorical = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
y_pred_categorical = np.array([[0.7, 0.2, 0.1], [0.1, 0.8, 0.1], [0.2, 0.2, 0.6]])
loss_categorical = categorical_cross_entropy_loss(y_true_categorical, y_pred_categorical)
print("Categorical Cross-Entropy Loss:", loss_categorical)
请注意，上述代码示例仅用于演示目的，实际使用中可能会使用深度学习框架提供的交叉熵损失函数，因为它们通常更加优化和稳定。例如，在TensorFlow中，可以使用tf.keras.losses.BinaryCrossentropy和tf.keras.losses.CategoricalCrossentropy类来计算二分类和多分类交叉熵损失函数。在PyTorch中，可以使用torch.nn.BCELoss和torch.nn.CrossEntropyLoss类来计算相应的损失函数。

代码来自于https://blog.csdn.net/qlkaicx/article/details/136100406

五.交叉熵函数优缺点

1.优点

在用梯度下降法做参数更新的时候，模型学习的速度取决于两个值：

1、学习率；

2、偏导值;

其中，学习率是我们需要设置的超参数，所以我们重点关注偏导值。从上面的式子中，我们发现，偏导值的大小取决于和，我们重点关注后者，后者的大小值反映了我们模型的错误程度，该值越大，说明模型效果越差，但是该值越大同时也会使得偏导值越大，从而模型学习速度更快。所以，使用逻辑函数得到概率，并结合交叉熵当损失函数时，在模型效果差的时候学习速度比较快，在模型效果好的时候学习速度变慢。

2.缺点

Deng在2019年提出了ArcFace Loss，并在论文里说了Softmax Loss的两个缺点：

1、随着分类数目的增大，分类层的线性变化矩阵参数也随着增大；
2、对于封闭集分类问题，学习到的特征是可分离的，但对于开放集人脸识别问题，所学特征却没有足够的区分性。对于人脸识别问题，首先人脸数目(对应分类数目)是很多的，而且会不断有新的人脸进来，不是一个封闭集分类问题。

另外，sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息，因为它采用了类间竞争机制，它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散。基于这个问题的优化有很多，比如对softmax进行改进，如L-Softmax、SM-Softmax、AM-Softmax等。