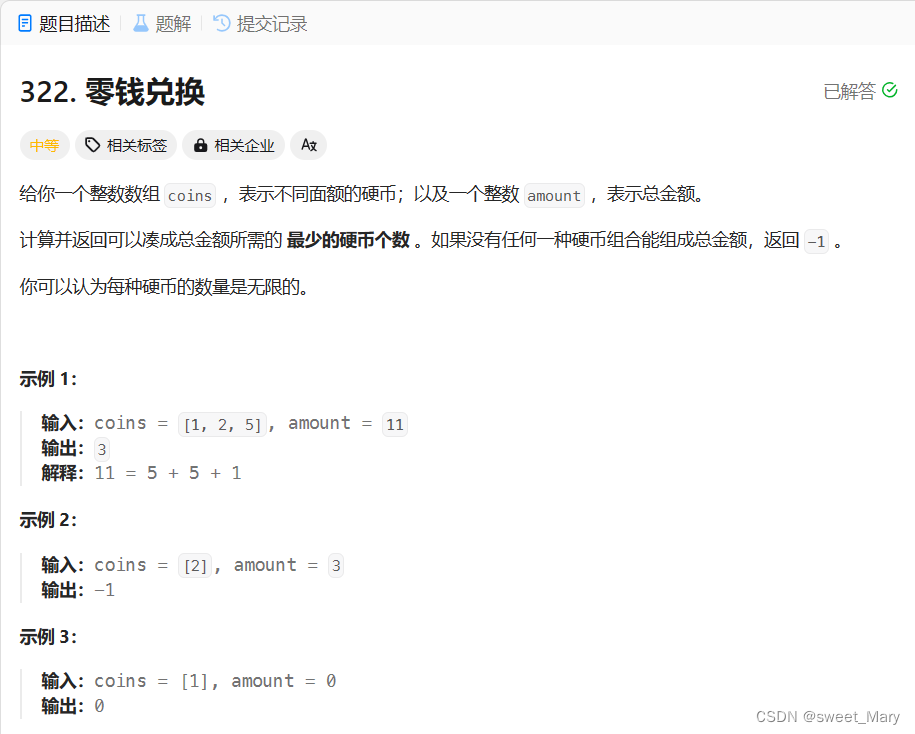
思路：

 这是一道典型的动态规划问题（希望下次不用提示，能直接认出来）：我将g[i]定义为总金币为i所需的最少硬币个数。所以递推公式可以表示为：g[i]=min(g[i-1],g[i-2],g[i-5])+1，也就是g[i]=min(g[i-coins[j])+1。数组初始化就是g[0]=0，g[coins[j]]=1。需要注意的是：

coins[i]的最大值是INT_MAX,所以我更习惯用LONG_MAX为g赋初值。其次，因为无法开很大的数组，同时注意到coins[i]>amount的部分是没有意义的，所以只需要开amount大的数组即可。

代码：

C++：

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<long> g(10010,LONG_MAX);
        int len=coins.size();
        //初始化
        g[0]=0;
        for(int i=0;i<len;i++){
            if(coins[i]>amount){continue;}
            else{g[coins[i]]=1;}
        }
        //dp   g[i]=min(g[i-coins[j]])+1
        for(int i=1;i<amount+1;i++){
            for(int j=0;j<len;j++){
                if(i-coins[j]>=0 && g[i-coins[j]]!=LONG_MAX){
                    g[i]=min(g[i],g[i-coins[j]]+1);
                }
            }
        }
        if(g[amount]==LONG_MAX){
            return -1;
        }
        else{return g[amount];}
    }
};

Python：

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        g=[float("inf")]*10010
        len_coins=len(coins)

        g[0]=0
        for i in range(len_coins):
            if coins[i]>amount:
                continue
            else:
                g[coins[i]]=1
        for i in range(1,amount+1):
            for j in range(len_coins):
                if i-coins[j]>=0 and g[i-coins[j]]!=float("inf"):
                    g[i]=min(g[i],g[i-coins[j]]+1)
        if g[amount]==float("inf"):
            return -1
        else:
            return g[amount]

明天将更新力扣---最长有小括号