Mamba的提出动机

最近非常火的语言模型都是Transformer模型。举几个例子，OpenAI的ChatGPT、谷歌的Gemini和GitHub的Copilot都是由Transformers驱动的。然而，transformer最大的问题是:它们都采用了注意力机制，而注意力随序列长度的二次增长。简单地说，对于快速交流(要求ChatGPT讲一个笑话)，这个还好。但对于需要大量单词的查询(要求ChatGPT总结100页的文档)，transformer的速度可能会慢得令人望而却步。Mamba就是致力于解决这个问题的。
Mamba比差不多大小的Transformer性能要更好，而且计算量和序列长度呈线性缩放。

Transformer

关于Transformer的介绍，具体可以看之前的一片博客：《详解注意力机制和Transformer》

Transformer 把文本的输入看成一个包含多个单词（token）的序列（sequence) 。

"Hello","!","My".. 这些单词或者符号代表一个token，组成在一起的句子就是一个sequence

Transforme的优点是：无论当前输入是什么，都可以回顾之前看到的所有Token。

在生成“is”时，transformer可以选择性的且独立的看到先前的单词，例如“My”和“Hello”

Transformer主要包括两个结构，一个是编码器（encoder）用来编码文本输入，一个是解码器（decoder）用来生成输出。

Transformer可以用在多种任务上，下图是Transform应用在文本翻译的例子

目前很火的生成式模型是只使用decoders结构，例如ChatGPT(Generative Pre-trained Transformers)

下图是生成式模型的一个例子

下面我们来看一个解码器的组成。Decoder是由一个masked self-attention和一个feed-forward neural network构成。

Decoder的组成

Self-attention 也是transformer的核心，它可以生成一个attention map 。attention map 是一个权重矩阵，用来存储每两个token之间相关性的大小。

attention map的示意图：每个token 和它自己的相关程度是最高的，如下图中对角线的元素颜色最深（表示相关性最高）； 我们还可以观察到“Matten”和“name”之间的相关性也比较高，而“Matten”和“is”之间的相关性就比较低。 ➡️ 更进一步解释：在生成当前的token （“Maarten”）时，"is"对于当前的生成的内容没有太大的帮助，而“name”可以指示当前生成的内容是一个名字。

在训练过程中，这个attention map的矩阵是可以并行生成的，因此可以加速训练。

⁉️ 为什么可以并行生成attention map呢？
我们可以参考《详解注意力机制和Transformer》 中的这个例子。在训练时，我们是预先知道完整的输入序列的。但是在预测时，我们只能看到先前输出的token，而看不到后续的token。

✔️Transformer的优点: 可以看到之前所有的序列，而且在训练过程中可以并行化计算。

🔗 [b.1]中的原表达： It enables an uncompressed view of the entire sequence with fast training. 这里的 uncompress的意思是：transformer计算序列中所有的token两两之间的相关性的大小。假设输入的序列中包含$n$个token, 得到的attention map的大小是$n\times n$。
☕举个例子，当我们在生成“Marten”这个单词时，可以查看attention map中记录的“Marten”和所有其他token {“My”,“name”,“is”}的相关性大小。而对于下文将要介绍的RNN和S4,Mamba模型而言，它们对其他token提供的信息进行概括性的压缩。

❌ Transformer的缺点：在推理过程中，每生成一个新的token，都需要重新为整个序列计算一个新的attention map，导致推理性能很慢。对于一个长度为$L$的序列，大约需要$L^2$的计算，如果序列长度增加，计算量会更大。

Transformer的推理过程

🔷 Transformer的性能总结：训练快，推理慢。

RNN

循环神经网络(RNN)是一种基于序列的网络。它在序列的每个时间步都需要两个输入，即时间步t的输入和前一个时间步t-1的隐藏状态，以生成下一个隐藏状态并预测输出。

RNN具有一种循环机制，将信息从上一步传递到下一步。下图中我们展开循环，进行可视化。

✔️RNN的优点：在生成当前的输出时，RNN只需要考虑当前的输入和上一时刻的隐藏状态。 和Transform相比，RNN不需要重新计算先前所有的隐藏状态。
换句话说，RNN可以快速进行推理，因为它的计算量与序列长度呈线性扩展。理论上，它甚至可以拥有无限长的上下文长度。

RNN中，每个隐藏状态都是之前所有隐藏状态的聚合，通常是一个压缩视图（compressed view）。

❌RNN的缺点：训练不能并行进行，因为它需要按照时间顺序地完成每个步骤。

RNN的推理和训练过程

❓ 为什么RCNN不能并行训练: 在反向传播过程中，RNN需要计算每个时间步的梯度，并且这些梯度需要沿着时间步依次传播回去。如果同时更新所有时间步的参数，会导致梯度混乱和不稳定。因此不能并行训练

🔷 RNN的性能总结：训练慢，但是推理快 （和Transformer恰恰相反~）

🐍: 我们能否以某种方式找到一种架构，既能像transformer一样并行训练，又能执行与序列长度线性扩展的推理? 这便是Mamba想要解决的问题。

Mama的提出背景

状态空间模型 (The State Space Model, SSM)

---

什么是状态空间 (State Space)？

☕举个例子，假如我们在走迷宫，那么状态空间（state space）就是我们在地图中所有可能的状态(states)， 包含{ 我们正在哪里？下一步可以往哪个方向走走？下一步我们可能在哪里？}

状态空间

描述状态的变量，在我们的例子中是X和Y坐标，以及到出口的距离，可以表示为“状态向量”。

状态向量

例如，当前的状态向量如下：

---

什么是状态空间模型（State Space Model, SSM）？
ssm是用于描述这些状态表示的模型，并根据某些输入预测其下一个状态可能是什么。

在时刻t, SSMs为:

• 映射输入序列x(t) -(例如，在迷宫中向左和向下移动)
• 到隐藏状态表示h(t) -(例如，到出口的距离和x/y坐标)
• 并推导出预测的输出序列y(t) -(例如，再次向左移动以更快地到达出口)

然而，SSM不是使用离散序列(如向左移动一次)，而是将连续序列作为输入，并预测输出序列。

SSM的输入是一个连续的序列，输出也是一个连续的序列

SSM假设动态系统，例如在3D空间中运动的物体，可以通过两个方程从其在时间$t$的状态进行预测。

第一行描述了状态方程，第二行描述了输出方程。这两个方程是SSM的核心。

---

图解状态方程和输出方程
状态方程：

状态方程图示：矩阵A和矩阵B分别控制着当前状态和输入如何影响状态的变化

输出方程：

输出方程图示：描述了状态如何转换为输出(通过矩阵C)以及输入如何影响输出(通过矩阵D)

上述的A，B，C，D都是可学习的参数

将上述的两个方程整合在一起，得到了如下的结构：

SSM的总体架构

接下来，我们逐步理解这些矩阵是如何影响学习过程。

Step1: 假设我们有一些输入信号x(t)，这个信号首先乘以矩阵B，矩阵B描述了输入如何影响系统。

Step 2: 矩阵A和当前状态相乘。矩阵A描述了内部状态之间是如何连接的。

Step 3：矩阵C和新的状态相乘。矩阵C描述了状态是如何转化到输出的。

最后，我们可以利用矩阵D提供一个从输入到输出的直接信号。这通常也称为跳跃连接(skip-connection)。

SSM通常被认为是不包含跳跃连接的部分。

回到我们简化的视角，可以看出矩阵A、B和C是SSM的核心。

与此同时，可以将原来的两个方程进行新的可视化。

这两个方程旨在从观测数据中预测系统的状态。由于预期输入是连续的，所以SSM的主要表示是连续时间表示（continuous-time representation）。

线性状态空间层 (Linear State-Space Layer, LSSL)

LSSL[a.2]的核心思想是把连续时间的SSM进行离散化，得到两种离散化的表示（循环形式和卷积形式）

---

将连续的信号转化为离散的信号
通常而言，我们的输入是离散的，例如一个文本序列。为了将离散的输入变成SSM可用的连续信号，我们使用零阶保持技术（Zero-order hold technique）。

零阶保持技术的原理：每次我们接收到一个离散信号时，我们都保持它的值，直到我们接收到一个新的离散信号。我们保存该值的时间由一个新的可学习参数表示，称为步长∆。

零阶保持技术（Zero-order hold technique）

现在我们有了一个连续的信号作为输入，我们可以生成一个连续的输出，并且只根据输入的时间步长对值进行采样。这个采样的值就是我们离散化的输出。

从数学的角度而言，我们可以按照如下的方式应用零阶保持技术

将矩阵A和B进行离散化

有几种有效的离散化方法，如欧拉方法、零阶保持器(Zero-order Hold, ZOH)方法或双线性方法。欧拉方法是最弱的，但在后两种方法之间的选择是微妙的。事实上，S4论文采用的是双线性方法，但Mamba使用的是ZOH。

我们从一个连续的SSM（函数到函数，x(t)→y(t)）到一个离散SSM（序列到序列，xₖ→yₖ）。

连续SSM和离散SSM的对比。我们使用k而不是t来表示离散的时间步长。

接下来我们看一下离散化SSM的两种表示形式

---

循环表示（Recurrent Representation）

在每个时间步长，我们计算当前输入(Bxₖ)如何影响前一个状态(Ahₖ₋₁)，然后计算预测输出(Chₖ)。

离散SSM的展开表示


我们可以发现这种循环的SSM结构和RNN非常的类似。

进一步的，我们将这种循环的SSM结构展开，进行可视化。

这使得我们可以将RNN的基本方法应用在离散的SSM上，但还需要考虑RNN推理快和训练慢的特性。

---

卷积表示（Convolution Representation）
在经典的图像识别任务中，我们使用卷积核来聚集特征。

类似的，因为我们处理的是文本而不是图像，所以我们需要一维卷积:

这个Kernel的具体表示如下：

接下来，我们逐步看一下这个Kernel是如何工作的

Step 1

Step 2

Step 3

将SSM表示为卷积的一个主要好处是，它可以像卷积神经网络(CNN)一样并行训练。然而，由于核大小固定，它们的推理不像RNN那样快速。

---

LSSL的设计思路

SSM的三种表示：连续时间（Continuous-time），循环(recurrent)，卷积(convolutional)

有了这些表示，我们可以使用一个巧妙的技巧，即根据任务选择一种表示。在训练过程中，我们使用可以并行化的卷积表示，在推理过程中，我们使用高效的循环表示。这种混合表示就被称为LSSL。

LSSL的一个重要特性是线性时间不变（Linear Time Invariance, LTI）
LTI声明SSM参数A、B和C对于所有时间步都是固定的。这意味着矩阵A、B和C对于SSM生成的每个token都是相同的。换句话说，无论你给SSM什么序列，A、B和C的值都保持不变。我们有一个不感知内容(not content-aware)的静态表示。

结构化序列空间模型 （Structured State Spaces for Sequences, S4）

Mamb的模型是基于S4模型构建的，所以我们先介绍下S4模型

S4是一个 线性时间不变的状态空间模型：linear time invariant (LTI) state space model (SSM)
矩阵A 捕获关于前一个状态的信息以构建新状态。

矩阵A本质上是用来产生隐藏状态的。

那么，我们应该如何创建矩阵A，使其可以保留更多的上下文信息呢？
这里使用的是High-order Polynomial Projection Operators (HiPPO) [a.3].
HiPPO试图将它迄今为止看到的所有输入信号压缩为一个系数向量

HiPPO使用矩阵A来构建状态表示，可以很好地捕获最近的token并衰减旧的token。其公式可以表示为:

假设矩阵A的大小是$4\times 4$, 那么它的HiPPO Matrix的表示如下：

使用HiPPO构建矩阵A比初始化为随机矩阵要好得多。因此，与旧信号(初始token)相比，它可以更准确地重建较新的信号(最近的token)。
HiPPO矩阵背后的想法是，它产生一个隐藏状态来记忆其历史。
从数学的角度而言，它通过跟踪Legendre多项式[a.4]的系数来实现这一点，这使得它可以近似之前的所有历史。

然后将HiPPO应用于我们之前看到的递归和卷积表示，以处理长程依赖关系。其结果是序列的结构化状态空间(Structured State Space for Sequences, S4)，这是一类可以有效处理长序列的SSM。

S4主要包括以下三个部分：

• 状态空间模型
• HiPPO用于处理远程依赖
• 用于创建循环和卷积表示的离散化

Mamba的介绍

🐍 Mamba是一种状态空间模型(SSM)架构，它改进了S4架构。它有时也被称为S6或者selective SSM，它对S4进行了两项重要修改:

• 选择性扫描算法(selective scan algorithm），允许模型过滤相关或者不相关的信息
• 硬件感知的算法(hardware-aware algorithm)，允许通过并行扫描(parallel scan)、核融合(kernel fusion)和重计算(recomputation)有效地存储(中间)结果。

---

Mamba 要解决什么问题？
SSM和S4无法选择性的关注指定的输入（the ability to focus on or ignore particular inputs）。

下面，我们举两个例子来说明这个问题。
☕Example 1: Selective Copying Task
在选择性复制任务中，SSM的目标是复制输入的一部分并按顺序输出.

Selective Copying 从输入中提取名词，然后按照顺序复制到输出中。

然而，(循环/卷积)SSM在这项任务中表现不佳，因为它是线性时间不变（Linear Time Invariant）的。正如我们之前看到的，矩阵A、B和C对于SSM生成的每个token都是相同的。
因此，SSM无法进行内容感知推理（content-aware reasoning），因为它将每个token视为固定的A、B和C矩阵的结果。这是一个问题，因为我们希望SSM对输入(提示)进行推理。

☕Example 2: Induction Heads
这个任务的目标是重现在输入中发现的模式。
本质上是在执行one-shot prompting，试图“教”模型在每个“Q:”之后提供一个“A:”响应。然而，由于ssm是时不变的，它无法选择从历史中回忆之前的哪个标记。

让我们以矩阵B为例来说明这一点。无论输入x是什么，矩阵B都是完全相同的，因此与x无关。

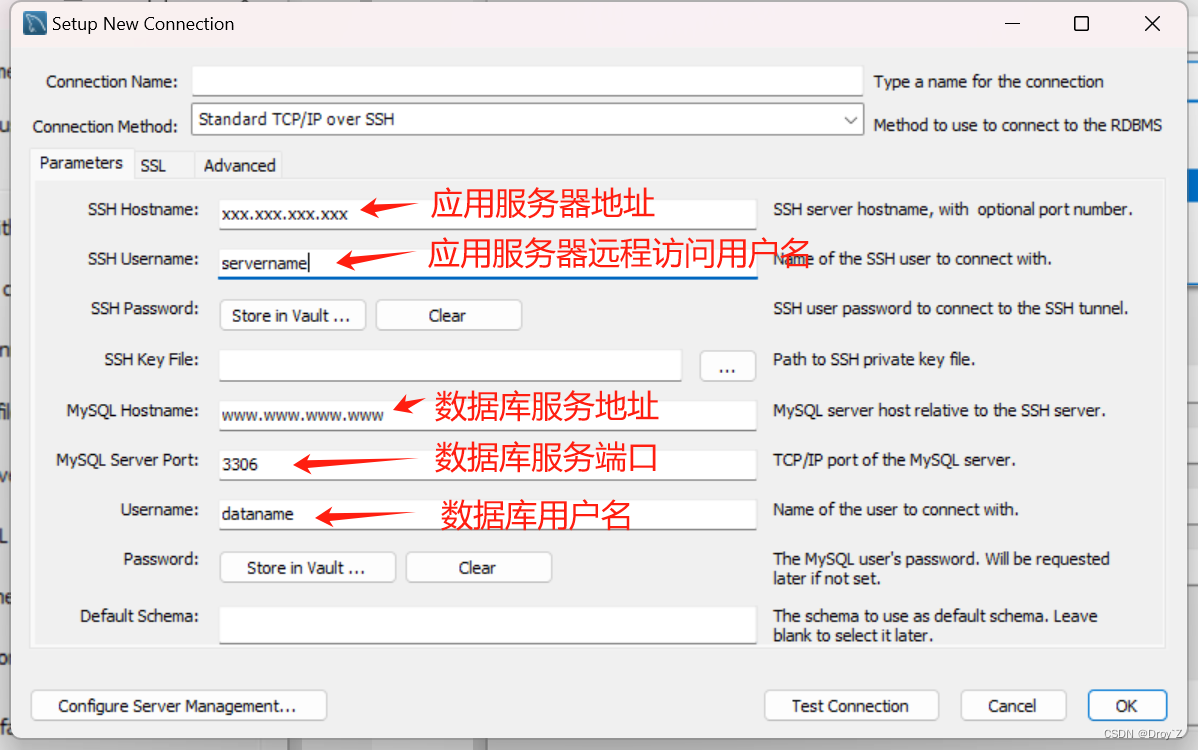
同样，无论输入是什么，A和C也保持固定。这表明了我们迄今为止看到的SSM都是静态的。

相比之下，这些任务对transformer来说相对容易，因为它们根据输入序列动态改变注意力。他们可以选择性地“看”或“关注”序列的不同部分。

SSM在这些任务上的糟糕表现说明了time-invariant SSM的潜在问题，矩阵A、B和C的静态性质导致了其无法进行内容感知（content-awareness）。

Mamba的特性一： 选择性的保留信息（Selective Retain Information）

SSM的循环表示创建了一个非常高效(more efficient)的小状态，因为它压缩了整个历史状态。然而，与没有压缩历史状态(通过attention map)的Transformer模型相比，它的性能要差的多（less powerful）。

Mamba 致力于保留一个小的且有用的状态信息， 兼顾性能和效率。

如上所述，它通过有选择地将数据压缩到状态中来实现这一点。（当有一个输入句子时，通常会有一些信息，比如标点，没有太多意义。这些无意义的信息就可以被忽略掉。）
为了有选择地压缩信息，我们需要参数依赖于输入。
为此，让我们首先探究下在训练过程中SSM的输入和输出维度:

SSM中Input和Output的维度：B表示batch size, L表示序列长度，D表示输入张量的大小。

在结构化状态空间模型(S4)中，矩阵A、B和C与输入无关，因为它们的维数N和D是静态的，不会改变。

相反，Mamba通过合并输入的序列长度和批次大小，使矩阵B和C，甚至步长∆依赖于输入:

这意味着对于每个输入标记，我们现在有不同的B和C矩阵，这解决了内容感知的问题。这样就可以依赖于输入，选择什么保持在隐藏状态，什么要忽略。

注意:矩阵A保持不变，因为我们希望状态本身保持静态，但它被影响的方式(通过B和C)是动态的。

更小的步长∆导致忽略特定的单词，而更多地使用前一个上下文，而更大的步长∆则更多地关注输入单词而不是上下文:

更进一步解释：当步长较小（即∆较小）时，模型更倾向于忽略特定的单词，而更多地依赖前一个上下文。这意味着模型更注重前面的单词对当前单词的影响，而忽略了较远距离的单词。
相反，当步长较大（即∆较大）时，模型更多地关注当前输入单词而不是上下文。这意味着模型更多地考虑当前输入单词对上下文的影响，而不是依赖于前一个上下文来决定当前单词的特征。

Mamba的特性二： 扫描操作（The Scan Operation）

上述的选择性保留信息也带来了一些问题：由于这些矩阵(B,C,∆)现在是动态的，它们不能使用卷积表示进行计算，因为它假设一个固定的核。我们只能使用递归表示，而失去了卷积提供的并行化。

为了实现并行化，让我们先来看看如何使用递归计算输出:

每个状态是前一个状态(乘以A)加上当前输入(乘以B)的和。这称为扫描操作，可以用for循环轻松计算。相比之下，并行化似乎是不可能的，因为只有在我们拥有前一个状态的情况下，每个状态才能计算出来。然而，Mamba通过并行扫描算法使这成为可能。

Mamba的特性三：硬件感知算法 （Hardware-aware Algorithm）

GPU的一个缺点是它们在小型但高效的SRAM和大型但略低效率的DRAM之间的传输(IO)速度有限。频繁地在SRAM和DRAM之间复制信息成为瓶颈。

与Flash Attention一样，Mamba试图限制从DRAM切换到SRAM的次数，反之亦然。它通过核融合来实现这一点，核融合允许模型防止写入中间结果，并持续执行计算，直到完成。

我们可以通过可视化Mamba的基本架构来查看DRAM和SRAM分配的具体实例:

这里将下列代码融合到一个内核中:

• 用∆离散化步长
• 选择性扫描算法
• 与C相乘

硬件感知算法的最后一部分是重计算 (recomputation)。
中间状态不保存，但对于反向传递计算梯度是必要的。相反，作者在反向传递期间重新计算这些中间状态。虽然这看起来效率不高，但与从相对较慢的DRAM读取所有中间状态相比，它的开销要小得多。

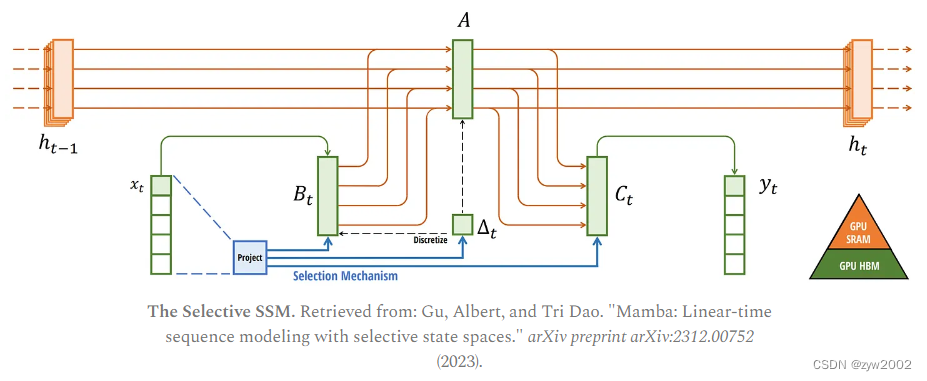
我们现在已经介绍了其架构的所有组件，下图是Mamba的Overview

• 首先，输入Xt通过选择性机制映射得到Bt，∆，Ct
• 然后使用∆，用零阶保持技术对A和Bt进行离散化
• 离散化后的B和输入Xt相乘，离散化后的A和原始状态$h_{t-1}$相乘，将这两项相加得到新的状态$h_t$。
• 新状态和Ct相乘，得到输出$y_t$

Selective SSM的示意图

Mamba基础块的设计（Mamba Block）

在Transformer中，用Decoder block来实现self-attention。与此类似，在Mamba中，也使用Mamba Block 来实现 selective SSM。

和解码器一样，我们可以将多个Mamba块堆叠起来，并将它们的输出作为下一个Mamba块的输入:

它首先用一个线性投影（linear projection）得到我们的输入嵌入（input embedding）。然后，在应用选择性SSM之前进行卷积，以防止独立token计算。

选择性SSM具有以下属性:

• 通过离散化创建循环SSM
• 在矩阵A上进行HiPPO初始化以捕获长程依赖关系
• 选择性扫描算法选择性地压缩信息
• 硬件感知算法加速计算

在查看代码实现时，我们可以进一步扩展此架构，并探索端到端的示例。变化包含normalization layers和用于选择输出标记的softmax。

总结：Mamba 即可以进行并行化训练，也可以按照线性缩放的复杂度进行推理，同时可以处理无限的上下文信息。

补充介绍

接下来，我们从数学公式的角度，更深入的了解上文中涉及的一些技术细节。

连续状态空间模型(SSM)定义了一个从输入信号(时间t的函数) $u(t)\in R^M$到输出信号$y(t)\in R^M$通过一个潜在状态$x(t)\in R^N$的线性映射:

式中$A(t)\in R^{N\times N},B(t)\in R^{N\times M},C(t)\in R^{M\times N}$。这些通常也被称为状态矩阵、输入矩阵和输出矩阵。

离散化方法

为了将连续的SSM变成离散的SSM，可以采用多种离散化的方法。
欧拉模型（Euler’s method） 是最简单的一种离散化方法。
把$x^{\prime }(t)=f(x(t))$转换成一阶近似的形式：$x_k=x_{k-1}+∆f(x_{k-1})$, 其中x表示状态，f表示状态转换函数。
然后将上式代入到（2.1a）中，可以得到：

这样我们就可以得到了离散化的状态参数：

然而，欧拉方法可以是不稳定。还有更精确的方法，如零阶保持(Zero-order Hold,ZOH)或双线性变换(bilinear transform, 也称为Tustin的方法)。

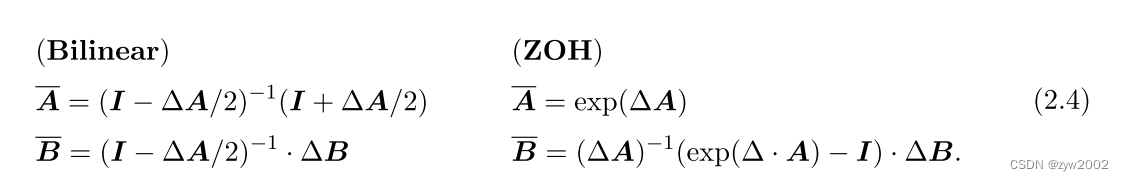
最后，我们再来总结下离散和连续的SSM

• 首先，得到离散的输入（左上图）
• 然后，通过离散化技术（例如零阶保持）得到连续的输入（右上图）
• 接着，输入到连续的SSM中，得到连续的输出（右下）
• 最后，对连续的输出进行采样，得到离散的输出（左下）
  

SSM的卷积表示推导

我们把SSM的状态推导公式展开：

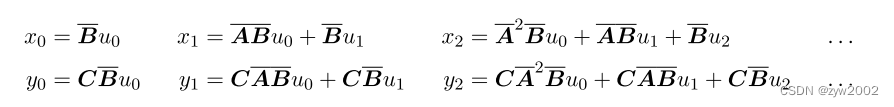
然后发现规律，得到$y_k$

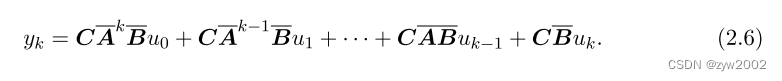
进一步的，我们可以用卷积核的形式来描述上式

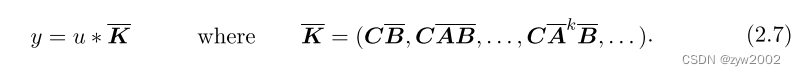
详细介绍HiPPO

建模长期和复杂的时间依赖关系的基本问题：记忆存储和合并来自以前时间步骤的信息。
然而，流行的机器学习模型很容易遗忘:它们要么是用固定大小的上下文窗口(例如注意力)构建的，要么是启发式机制，根据经验，它们受到记忆范围有限的影响(例如，由于"梯度消失")。

HiPPO Framework (High-Order Polynomial Projection Operator)
问题定义：给定任意一个输入函数$f(t)$,寻找一个coefficient vectors $c(t)$, 它用来压缩所有的历史记忆。
一个很直接的方法 就是用多项式去拟合$f(t)$，随着时间的推移我们需要不断的更新多项式的系数。

HiPPO框架。输入函数f(t)（黑线）通过存储其根据指定measure（彩色框）的最佳多项式投影的系数（彩色线）持续近似。这些系数随时间演变（红色、蓝色），遵循线性动态系统

简而言之，HiPPO框架采用一组measure，并给出一个带有封闭形式转移矩阵的方程，这些矩阵为A(t)，B(t)。这些矩阵依赖于measure，根据这些动态找到系数c(t)，这些系数最佳地近似了f(t)的历史。

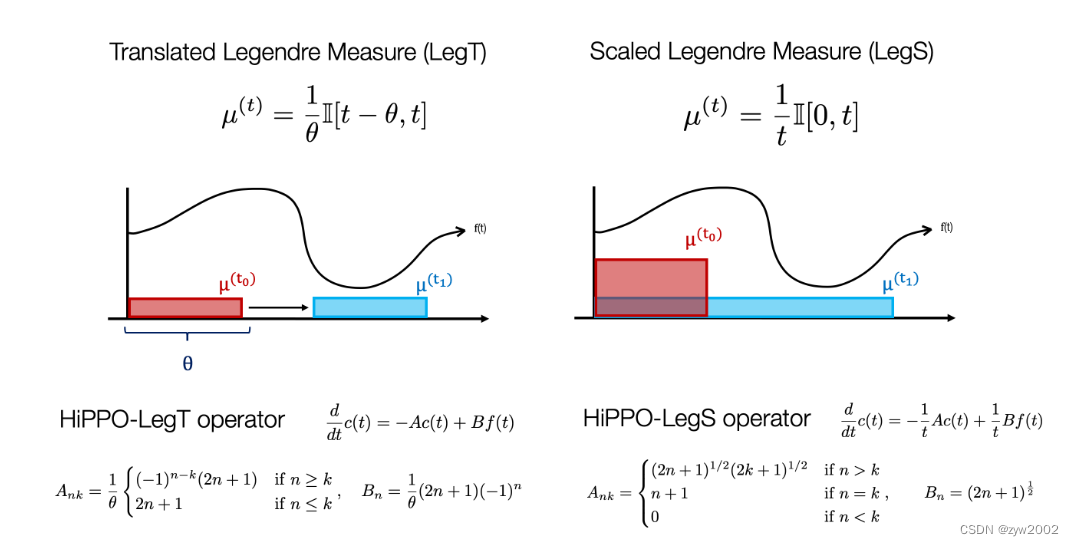
☕ 下面，我们举两个measure的实例来进一步的解释HiPPO

左图（Translated Legendre measure）采用了固定长度的滑动窗口，换句话说，它关注最近的历史信息。
右图 （scaled Legendre measure）将整个历史均匀加权到当前时间。

简单的measure及其对应的HiPPO运算符示例。Translated Legendre Measure统一加权过去θ（一个超参数）个时间单位，而Scaled Legendre Measure统一加权所有历史。

HiPPO是一个简单的线性递归，可以以许多方式集成到端到端模型中，在这里我们将HiPPO集成到RNN中。

上图是HiPPO的离散化表达形式 下图是HiPPO-RNN的图示

进一步理解Mamba的selective 特性

因为S4没有选择性，它被迫以完全相同的方式对待所有输入部分。然而，当你在阅读一个句子时，有些单词不可避免地比其他单词更重要。假设我们有一个模型，它可以根据意图对句子进行分类，我们给它一个句子:“I want to order a hamburger”如果没有选择性，S4在处理每个单词时花费的“精力”是相同的。

但如果是一个试图对这个句子的意图进行分类的模型，你可能希望更多地“关注”某些单词而不是其他单词。“想要”和“去”这两个词到底对句子的潜在含义没有太大的贡献。实际上，如果我们能把有限的精力更多地花在“订单”和“汉堡”这样的词上，就能知道用户想要做什么，知道用户在点什么。通过使模型参数成为输入的函数，Mamba使“关注”输入中对手头任务更重要的部分成为可能。

进一步理解Mamba中的并行扫描

首先，我们举一个累加前缀和的例子。

计算序列[4,1,5,3,9,2]的累加前缀和

我们可以把这个任务用RNN模式的Mamba来表示。
$$h_t=h_{t-1}+x_t$$。这个公式形成了一个递归式:在每一步，我们通过将前一个存储值与当前输入相加来计算新值。

现在，让我们再次看一下更新Mamba的隐藏状态的递归式。
$$h_t=\bar{A}{h}_{t-1}+\bar{B}{x}_t$$
可以发现这两个公式的结构是非常相似的。
虽然计算前缀和在本质上似乎是顺序的，但我们实际上有高效的并行算法来完成这项任务!在下图中，我们可以看到并行前缀和算法的运行，其中每条垂直线表示数组中的一项。

参考文献

---

A.本博客参考的论文：
[a.1] Mamba: 《Mamba: Linear-Time Sequence Modeling with Selective State Spaces》
[a.2] Linear State-Space Layer (LSSL): 《Combining Recurrent, Convolutional, and Continuous-time Models with Linear State Space Layers》
[a.3]HiPPO《HiPPO: Recurrent Memory with Optimal Polynomial Projections》
[a.4] Legendre polynomial 《Legendre Memory Units: Continuous-Time Representation in Recurrent Neural Networks》
[a.5] Structured State Space for Sequences(S4)《Efficiently Modeling Long Sequences with Structured State Spaces》
[a.6]Simplified State Space Layers for Sequence Modeling(S5) 《Simplified State Space Layers for Sequence Modeling》

---

B. 本博客参考的讲解：

[b.1] 本文主要参考的Mamba的可视化图解：https://maartengrootendorst.substack.com/p/a-visual-guide-to-mamba-and-state
[b.2] HiPPO的讲解：https://hazyresearch.stanford.edu/blog/2020-12-05-hippo
[b.3] S4的讲解: The Annotated S4
[b.4] 另外一个Mamba的讲解,更多的偏向于数学的角度 Mamba No. 5 (A Little Bit Of…)
[b.5]一本超级详细的书，从数学的角度介绍了很多SSM系列模型 《MODELING SEQUENCES WITH STRUCTURED STATE SPACES》
[b.6] 从直觉的角度理解MambaMamba: The Easy Way
[b.7] 从代码的角度讲解Mamba的实现Mamba: The Hard Way
[b.8] 补充一个S4的讲解Structured State Spaces: Combining Continuous-Time, Recurrent, and Convolutional Models
[b.9] CSDN的一篇博客，介绍的很详细SSM、HiPPO、S4到Mamba

---

C. 视频讲解
[c.1] NeurIPS-Spotlight-HiPPO
[c.2] YouTube-Mamba Paper Explained
[c.3] Bilibili-Mamba 论文速读
[c.4] YouTube-S4 Explained

---

D. 代码
[d.1]Mamba的官方代码https://github.com/state-spaces/mamba