Day17｜二叉树part04：110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和、543: 二叉树的直径、124: 二叉树的最大路径和

news2025/11/1 7:14:54

之前的blog链接：https://blog.csdn.net/weixin_43303286/article/details/131982632?spm=1001.2014.3001.5501

110.平衡二叉树

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。
思路：递归求两个子树高度，一旦不满足平衡了，就把该节点的高度设置为-1；
一旦子树中有-1，那么本身肯定不是二叉平衡树了，直接返回-1；
如果还是，更新高度为Math.max(left, right) + 1;

class Solution {
    private int getHeight(TreeNode node){
        if(node == null){
            return 0;
        }
        int left = getHeight(node.left);
        if(left==-1){
            return -1;
        }
        int right = getHeight(node.right);
        if(right == -1){
            return -1;
        }
        if(Math.abs(left - right) > 1){
            return -1;
        }
        return Math.max(left, right) + 1;


    }
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }

        return getHeight(root) != -1;
    }
}

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

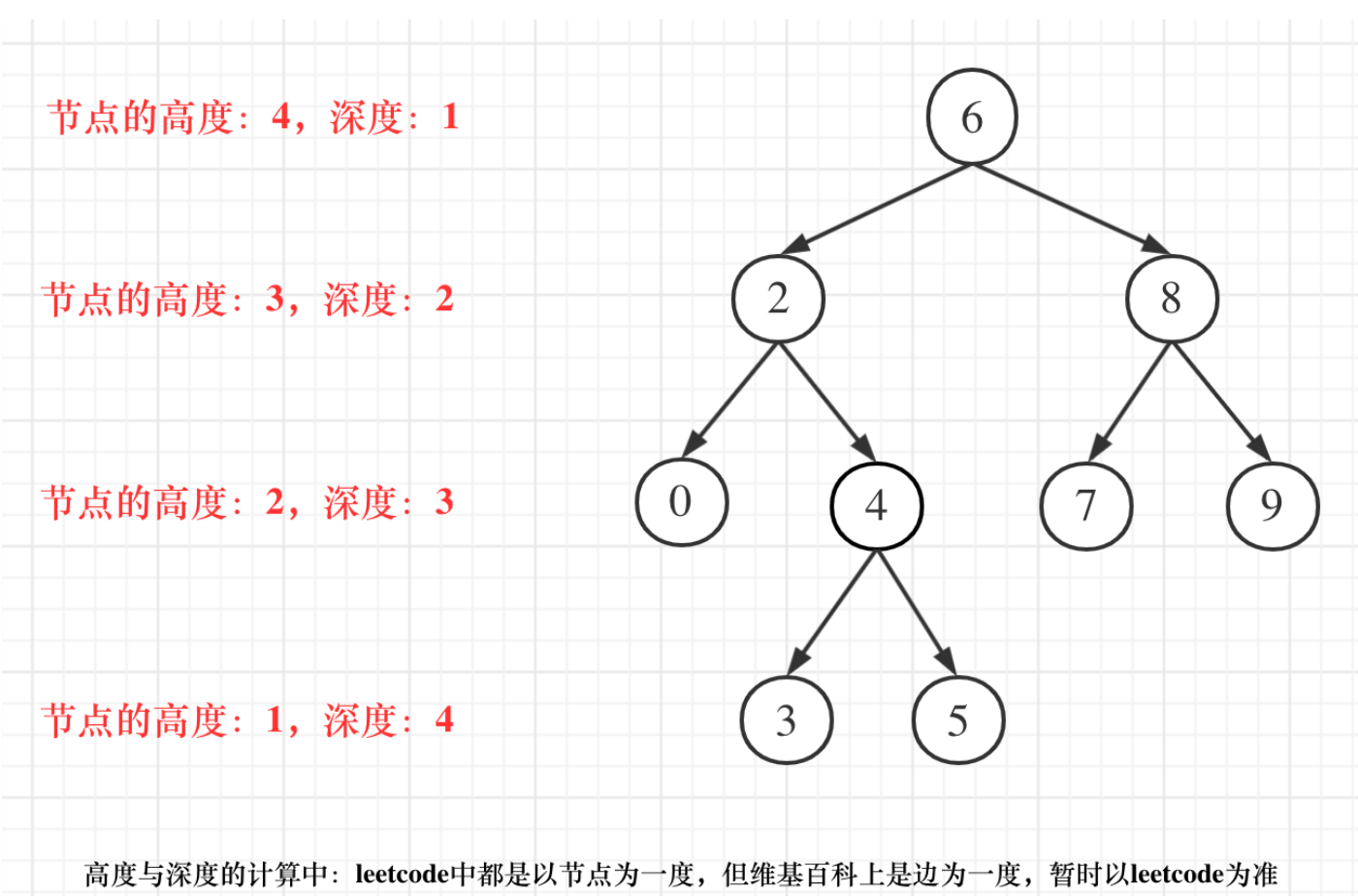
（高度：从下往上，深度：从上往下）

关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准（毕竟要在这上面刷题）。

257.二叉树的所有路径

class Solution {
    private List<String> res = new ArrayList<>();
    private StringBuilder sb = new StringBuilder();
    private void traversal(TreeNode node){
        if(node == null){
            return;
        }
        int length = sb.length();
        sb.append(node.val);
        if(node.left == null && node.right == null){
            res.add(sb.toString());
        }
        sb.append("->");
        traversal(node.left);
        traversal(node.right);
        sb.setLength(length);
    }
    public List<String> binaryTreePaths(TreeNode root) {
        traversal(root);
        return res;
    }
}

java中String无法修改，于是提供了StringBuffer进行字符串的相关操作，使用toString（）方法转化为String；
这里需要回溯，回溯的方法就是恢复sb到原来的length：

你需要在每次递归调用前后，分别添加和删除当前节点的值，以保证 StringBuilder 对象 sb 在每次递归返回后都能恢复到调用前的状态。这种技术被称为回溯。

终止条件应该是node==null：

如果我们选择的终止条件是节点是叶子节点，那么在遍历到叶子节点时，我们还会尝试去遍历它的左子节点和右子节点，这将导致我们尝试去访问 null 节点的左右子节点，从而可能出现空指针异常

记得添加箭头的位置。

404.左叶子之和

class Solution {
    private int res = 0;

    private void traversal(TreeNode node){
        if(node == null){
            return;
        }
        if(node.left != null && node.left.left == null && node.left.right == null){
            res += node.left.val;
        }
        traversal(node.left);
        traversal(node.right);
    }
    public int sumOfLeftLeaves(TreeNode root) {
        traversal(root);
        return res;
    }
}

关键是这么判断左叶子：从父节点出发，判断父节点的左节点是否是叶子结点。

543. 二叉树的直径

class Solution {
    private int ans = 0;
    private int traversal(TreeNode node){
        if(node == null){
            return 0;
        }
        int L = traversal(node.left);
        int R = traversal(node.right);
        ans = Math.max(L + R + 1, ans);
        return Math.max(L, R) + 1;
    }
    public int diameterOfBinaryTree(TreeNode root) {
        traversal(root);
        return ans - 1;
    }
}

这里为什么ans要 - 1：

ans 是所有节点的左子树深度与右子树深度之和的最大值。但是这个值实际上是节点的数量，而不是边的数量。在二叉树中，n个节点的路径长度是n-1（因为路径长度是由边来定义的，而一个路径上的边总是比节点少1）

124. 二叉树的最大路径和(Hard)

class Solution {
    int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }

    public int maxGain(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node.val + leftGain + rightGain;

        // 更新答案
        maxSum = Math.max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node.val + Math.max(leftGain, rightGain);
    }
}