在计算机科学中，分治法是一种解决问题的策略，它将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之，从而解决整个问题。这种方法在排序算法中得到了广泛应用，其中最具代表性的就是归并排序算法。

一、分治法与归并排序概述

归并排序是一种典型的分治思想的体现。它采用递归的方法，将待排序的序列不断划分为更小的子序列，直到子序列的长度为1（此时可以认为子序列已经有序），然后将这些有序的子序列合并成一个大的有序序列。

归并排序的主要步骤包括：

分解：将待排序的序列分解成若干个子序列，每个子序列的长度尽可能相等。
递归求解：对每个子序列进行归并排序，直到子序列长度为1。
合并：将排序好的子序列合并成一个有序的序列。
归并排序的时间复杂度为O(nlogn)，其中n为待排序序列的长度。这是因为每次递归分解都会将序列长度减半，而合并操作的时间复杂度与序列长度成正比。因此，归并排序是一种非常高效的排序算法。

二、归并排序的C语言实现

下面是一个简单的归并排序算法的C语言实现：

c
#include <stdio.h>

// 合并两个有序数组
void merge(int arr[], int l, int m, int r) {
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;

// 创建临时数组  
int L[n1], R[n2];  

// 拷贝数据到临时数组L[]和R[]  
for (i = 0; i < n1; i++)  
    L[i] = arr[l + i];  
for (j = 0; j < n2; j++)  
    R[j] = arr[m + 1 + j];  

// 合并临时数组回arr[l..r]  
i = 0;  
j = 0;  
k = l;  
while (i < n1 && j < n2) {  
    if (L[i] <= R[j]) {  
        arr[k] = L[i];  
        i++;  
    } else {  
        arr[k] = R[j];  
        j++;  
    }  
    k++;  
}  

// 拷贝L[]的剩余元素  
while (i < n1) {  
    arr[k] = L[i];  
    i++;  
    k++;  
}  

// 拷贝R[]的剩余元素  
while (j < n2) {  
    arr[k] = R[j];  
    j++;  
    k++;  
}  

}

// 归并排序函数
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// 找到中间点
int m = l + (r - l) / 2;

    // 对左边子数组进行归并排序  
    mergeSort(arr, l, m);  

    // 对右边子数组进行归并排序  
    mergeSort(arr, m + 1, r);  

    // 合并两个已排序的子数组  
    merge(arr, l, m, r);  
}  

}

// 测试函数
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr) / sizeof(arr[0]);

printf("Given array is \n");  
for (int i = 0; i < arr_size; i++)  
    printf("%d ", arr[i]);  

mergeSort(arr, 0, arr_size - 1);  

printf("\nSorted array is \n");  
for (int i = 0; i < arr_size; i++)  
    printf("%d ", arr[i]);  

return 0;  

}
这段代码首先定义了一个merge函数，用于合并两个已排序的子数组。然后，定义了一个mergeSort函数，用于递归地对子数组进行归并排序。最后，在main函数中，我们创建了一个待排序的数组，并调用mergeSort函数对其进行排序。排序完成后，我们打印出排序后的数组。

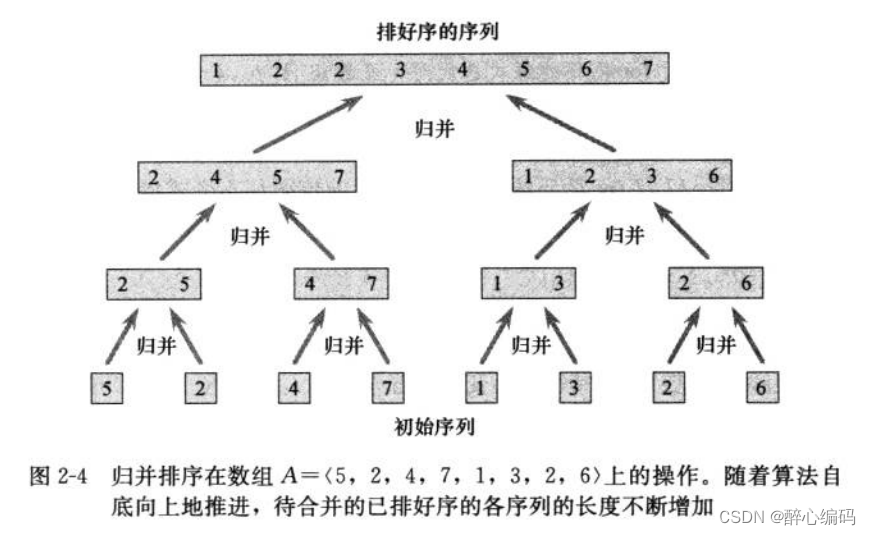
三、归并排序的性能分析

归并排序算法以其稳定的时间和空间性能在计算机科学中占据了一席之地。以下是关于归并排序的一些性能分析：

时间复杂度：

最好情况：O(nlogn)
最坏情况：O(nlogn)
平均情况：O(nlogn)
无论输入数据的顺序如何，归并排序的时间复杂度始终为O(nlogn)。这是因为归并排序总是会将数组拆分为尽可能均等的两部分，然后逐层合并，每一层的合并操作时间复杂度都是线性的，而层数为logn。

空间复杂度：

额外空间复杂度：O(n)
归并排序需要额外的空间来存储临时数组。在合并两个子数组时，需要创建一个与待排序数组等大的临时数组来存储数据。因此，归并排序的空间复杂度为O(n)。

稳定性：
归并排序是一种稳定的排序算法。稳定性意味着当两个元素的值相等时，它们在排序后的相对位置不会改变。归并排序在合并两个子数组时，会保留相等元素的原始顺序，从而保证了稳定性。

应用场景：
归并排序适用于需要稳定排序的场景，尤其是当数据量较大时。它也常用于外部排序，即当数据量太大以至于无法一次性加载到内存中时，归并排序可以分批处理数据，然后将有序的结果合并成一个完整的有序序列。

四、归并排序的优化

尽管归并排序的时间复杂度已经相当优秀，但在实际应用中，还可以通过一些优化来进一步提升性能：

非递归实现：
归并排序的递归实现虽然直观易懂，但在递归深度较大时，可能会导致函数调用栈的开销较大。为了避免这种开销，可以使用非递归（迭代）的方式来实现归并排序。非递归实现通常使用显式的栈结构来模拟递归过程。

二路归并改为多路归并：
传统的归并排序是二路归并，即将数组分成两部分进行归并。可以将二路归并扩展为多路归并，即每次将数组分成更多的部分进行归并。多路归并可以减少归并的次数，从而加快排序速度。但需要注意的是，多路归并会增加合并操作的复杂性。

减少辅助数组的使用：
在归并排序中，通常需要使用一个与原始数组等大的辅助数组来存储合并后的结果。为了减少空间开销，可以尝试使用一些技巧来减少辅助数组的使用。例如，在合并两个子数组时，可以先将左半部分的数据复制到辅助数组中，然后从右半部分开始向左半部分合并数据。这样，只需要一个额外的辅助数组即可完成合并操作。但需要注意的是，这种方法可能会增加数据复制的开销。

通过以上优化措施，可以进一步提升归并排序算法的性能和效率。不过，在实际应用中，需要根据具体的数据规模和要求来选择合适的优化策略。