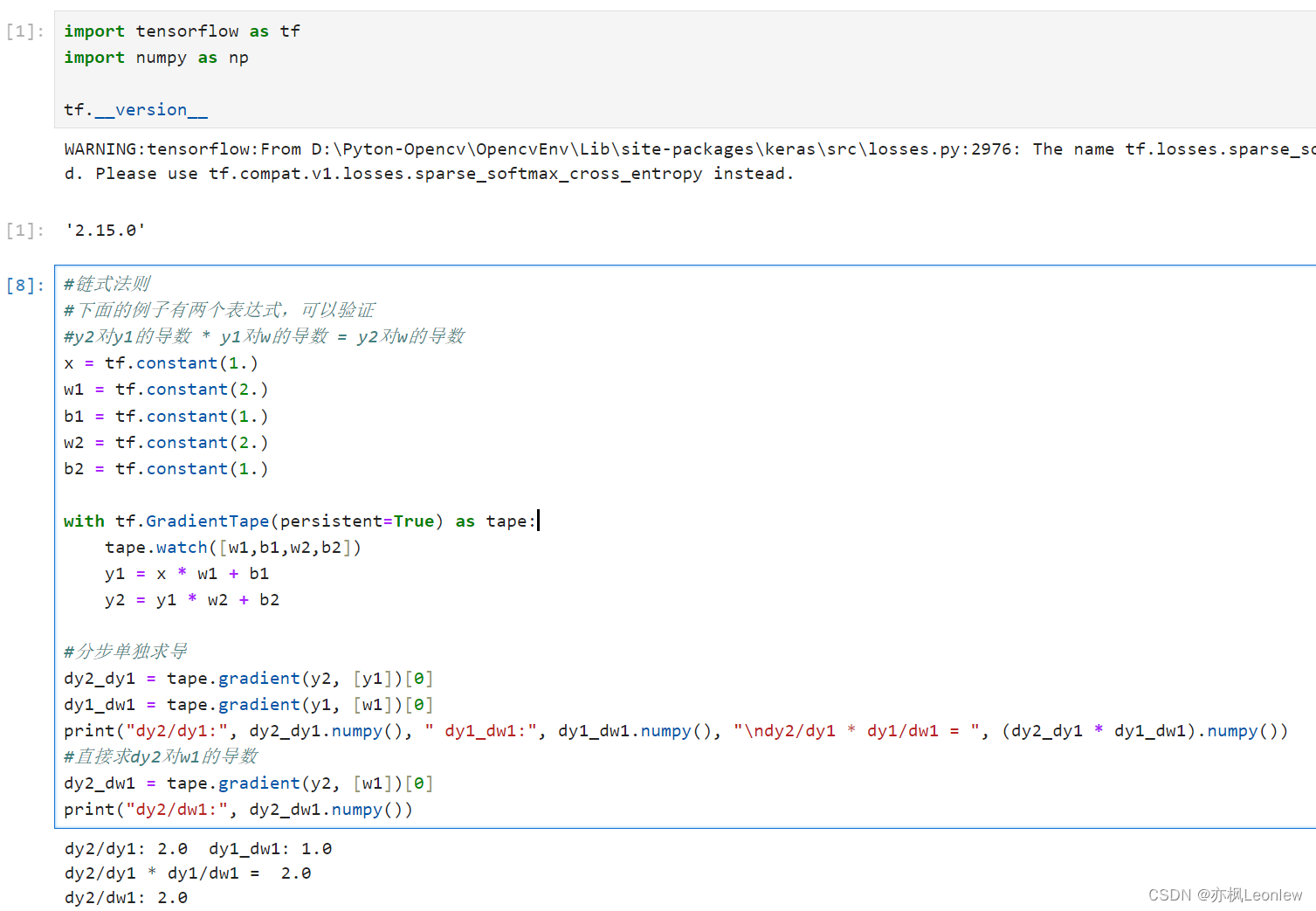
比赛链接
这场。。。好像已经是一周之前的比赛来着,终于补完了。
C是个披着字符串外衣的数学容斥题。D是个超级超级暴力的爆搜,写起来超级麻烦,感觉。。。真是一次酣畅淋漓的赤石。E是个DP,朴素想法其实比较直观,不过优化起来就很抽象了。F图论dfs跑一下就可以了,意外的简单。
一个我觉得讲的很好的视频讲解A-G(评论区里面有博客链接,放着讲解和代码)
A - Leftrightarrow
题意:
您将得到一个由“<”、“=”和“>”组成的字符串 S S S 。
判断 S S S 是否为双向箭头字符串。
字符串 S S S 是双向箭头字符串,当且仅当存在正整数 k k k ,使得 S S S 是一个“<”、 k k k “=`s和一个”>"的连接,按此顺序,长度为 ( k + 2 ) (k+2) (k+2) 。
思路:
判断一下给定字符串是不是第一个是 <,最后一个是 >,中间全是 = 就行了。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
string s;
int main(){
cin>>s;
if(s[0]=='<' && s[s.length()-1]=='>' &&
s.substr(1,s.length()-2).find_first_not_of("=")==string::npos)
puts("Yes");
else puts("No");
return 0;
}
B - Integer Division Returns
题意:
如果给定一个介于 − 1 0 18 -10^{18} −1018 和 1 0 18 10^{18} 1018 之间的整数 X X X ,则打印 ⌈ X 10 ⌉ \left\lceil \dfrac{X}{10} \right\rceil ⌈10X⌉ 。
这里, ⌈ a ⌉ \left\lceil a \right\rceil ⌈a⌉ 表示不小于 a a a 的最小整数。
思路:
C++的整数除法是向零取整,换句话说,对正数是向下取整,对负数是向上取整。
code:
#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;
ll x;
int main(){
cin>>x;
if(x<0)cout<<x/10;
else cout<<(x+9)/10;
return 0;
}
C - One Time Swap
题意:
您将得到一个字符串 S S S 。查找执行以下操作恰好一次可产生的不同字符串数。
- 设 N N N 为 S S S 的长度。选择一对整数 ( i , j ) (i,j) (i,j) ,例如 1 ≤ i < j ≤ N 1\leq i \lt j\leq N 1≤i<j≤N ,并交换 S S S 的第 i i i 和第 j j j 个字符。
可以证明,在这个问题的约束条件下,你总是可以执行它。
思路:
暴力枚举交换的两个位置,并统计所有不同的串肯定是不行的。考虑怎么样会产生一次不同的串也很麻烦。所以正难则反,考虑怎么交换是会重复的,并用总的交换方式减去重复的即可。
不难发现相同字符交换的话得到的就是原串,这时候是重复的。所以我们统计每种字符出现的次数,用总的选择数减去每种字符从中选两个的选择数即可。
不过需要注意的是,一开始的串并没有算上,所以第一次相同字母交换得到的和原串相同的串也是会产生一次贡献,特判一下即可。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;
typedef long long ll;
string s;
map<char,ll> mp;
ll n,ans;
int main(){
cin>>s;
for(auto x:s)mp[x]++;
n=s.length();
ans=n*(n-1)/2;
bool flag=false;
for(auto t:mp){
ll x=t.second;
if(!flag && x>1){
ans+=1;
flag=true;
}
ans-=x*(x-1)/2;
}
cout<<ans;
return 0;
}
D - Tiling
题意:
存在 H H H 行和 W W W 列的网格,每个单元具有 1 1 1 的边长,
我们有 N N N 个瓷砖。
第 i i i 块( 1 ≤ i ≤ N 1\leq i\leq N 1≤i≤N )是一个大小为 A i × B i A_i\times B_i Ai×Bi 的矩形。
确定是否可以将瓷砖放置在网格上,以便满足以下所有条件:
- 每个单元格都被正好一块瓷砖覆盖。
- 可以有未使用的瓷砖。
- 放置时,瓷砖可以旋转或翻转。
但是,每个瓷砖必须与网格的边缘对齐,而不会延伸到网格之外。
思路:
发现 H , W , N H,W,N H,W,N 非常小,考虑直接暴力。
先枚举所有的选取情况,然后对每种选取情况尝试放置在网格上。放某块砖的时候直接暴力枚举每个位置(假设枚举的位置是瓷砖的左上角),然后枚举旋转情况(因为是矩形,旋转两次 90 ° 90\degree 90° 相当于不旋转,翻转相当于没动,因此我们只需要验证不旋转和旋转一次 90 ° 90\degree 90° 即可)
这里可以稍微加个剪枝,就是对一种选取情况,选到的砖的总面积一定等于 H ∗ W H*W H∗W。
code:
看着长,其实逻辑并不复杂,但是不妨碍这是一道粪题。
#include <iostream>
#include <cstdio>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
int n,h,w;
pair<int,int> a[15];
bool pick[15];
bool vis[15][15];
bool checkprint(int x,int y,int idx){//检查是否可以放这块瓷砖
if(x+a[idx].first-1>h || y+a[idx].second-1>w)return false;
for(int i=x;i<x+a[idx].first;i++)
for(int j=y;j<y+a[idx].second;j++)
if(vis[i][j])
return false;
return true;
}
void print(int x,int y,int idx,bool st){//放/移除 这块瓷砖
for(int i=x;i<x+a[idx].first;i++)
for(int j=y;j<y+a[idx].second;j++)
vis[i][j]=st;
}
bool checkprint2(int x,int y,int idx){//旋转90°再放
if(x+a[idx].second-1>h || y+a[idx].first-1>w)return false;
for(int i=x;i<x+a[idx].second;i++)
for(int j=y;j<y+a[idx].first;j++)
if(vis[i][j])
return false;
return true;
}
void print2(int x,int y,int idx,bool st){//旋转90°再放
for(int i=x;i<x+a[idx].second;i++)
for(int j=y;j<y+a[idx].first;j++)
vis[i][j]=st;
}
vector<int> tt;
bool dfs2(int idx){//尝试放第idx块瓷砖
if(idx>=(int)tt.size()){
return true;
}
// cout<<idx<<endl;
for(int x=1;x<=h;x++){
for(int y=1;y<=w;y++){
if(vis[x][y])continue;
if(checkprint(x,y,tt[idx])){
print(x,y,tt[idx],1);
if(dfs2(idx+1))return true;
print(x,y,tt[idx],0);
}
if(a[tt[idx]].first!=a[tt[idx]].second && checkprint2(x,y,tt[idx])){
print2(x,y,tt[idx],1);
if(dfs2(idx+1))return true;
print2(x,y,tt[idx],0);
}
}
}
return false;
}
bool check(){//剪枝&检查这个旋转情况
int tot=0;
for(int i=1;i<=n;i++)
if(pick[i])
tot+=a[i].first*a[i].second;
if(tot!=h*w)return false;
tt.clear();
for(int i=1;i<=n;i++)
if(pick[i])
tt.push_back(i);
return dfs2(0);
}
void dfs(int idx){//枚举选举情况
if(idx>n){
if(check()){
puts("Yes");
exit(0);
}
return;
}
pick[idx]=true;
dfs(idx+1);
pick[idx]=false;
dfs(idx+1);
}
int main(){
cin>>n>>h>>w;
for(int i=1;i<=n;i++){
cin>>a[i].first>>a[i].second;
}
sort(a+1,a+n+1,[&](pair<int,int> a,pair<int,int> b){return a.first*a.second>b.first*b.second;});
dfs(1);
puts("No");
return 0;
}
E - Colorful Subsequence
题意:
有 N N N 个球排成一排。
左起第 i i i 个球的颜色为 C i C_i Ci ,值为 V i V_i Vi 。Takahashi想要从这一行中删除精确的 K K K 个球,以便在剩余的球的排列中,没有两个相邻的球具有相同的颜色。
高桥希望在不改变顺序的情况下,将这一行中的 K K K 个球移除,这样在排列剩余的球时,就不会有相邻的两个球颜色相同。此外,在此条件下,他希望最大化这一行中剩余球的总价值。
请计算高桥是否能移除 K K K 个球,使剩下的一行中没有相邻的两个球颜色相同。如果可以,求剩余球的最大总值。
思路:
朴素的动态规划思路还是比较好想的。即设 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k] 表示前 i i i 个球删掉 j j j 个,最后一个球的颜色为 k k k 的最大剩余价值。枚举到第 i i i 个球时,可以通过删掉或者不删掉第 i i i 个球来转移,删掉则从 d p [ i − 1 ] [ j − 1 ] [ k ] dp[i-1][j-1][k] dp[i−1][j−1][k] 转移过来,不删掉则从 d p [ i − 1 ] [ j ] [ k ′ ] dp[i-1][j][k'] dp[i−1][j][k′] 转移过来( k ′ k' k′ 表示所有非 c i c_i ci 颜色的颜色)。
不过时间复杂度为 N ∗ K ∗ N N*K*N N∗K∗N 的,肯定爆掉了 。发现其实我们不需要知道那么多颜色的答案,因为我们只要保证转移过来时不撞颜色就行,所以要么是从最大价值的颜色转移过来,要么从除了这个颜色以外剩下的最大价值转移过来。因此我们第三维只需要存储最大的价值和颜色,以及除了这个颜色以外的最大的价值和颜色,这样时间复杂度就优化到了 N ∗ K ∗ 2 N*K*2 N∗K∗2。
不过这时候空间复杂度也为 N ∗ K ∗ 2 N*K*2 N∗K∗2,会 M L E MLE MLE。考虑到我们第一维推到第 i i i 个位置的时候,它只和第 i − 1 i-1 i−1 个位置的 d p dp dp 值有关,所以我们可以用滚动数组的思想来优化:我们只存储前一个位置和现在要推的位置的 d p dp dp 值即可。
话说得轻巧,但是写起来超级麻烦 ,真是一场畅快淋漓的赤石啊!
如果我们第三位存储两种颜色,即最大价值的颜色和次大价值的颜色,那么我们需要另开一个长度为
2
2
2 的颜色数组来存,然后我们更新答案的时候,就需要考虑到:尝试更新最大价值但是颜色冲突,更新最大价值但是颜色不冲突 ,更新次大价值但是颜色冲突,更新次大价值但是颜色不冲突。然后呢,更新最大价值的时候还要顺便更新次大情况,还要考虑到无解的情况。写到大脑空空,两眼逐渐智慧起来。
然后没办法去借鉴题解了。
题解写法确实好 。我们不把颜色放在第三维度,而是把颜色当作一个信息,与最大价值一起存储起来,把所有可能的信息都存储在 d p dp dp 下。具体来说,设 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示前 i i i 个球删掉 j j j 个的 所有 最大价值和最后一个球的颜色。代码实现如下:
typedef long long ll;
#define pll pair<ll,ll>
const vector<pll> infv={{-inf,-1},{-inf,-2}};
vector<vector<vector<pll> > > dp(2,vector<vector<pll> >(k+1,infv));
这串代码可以理解为一个二维的 v e c t o r vector vector,然后它存储的“值”是 v e c t o r < p l l > vector<pll> vector<pll>, p l l pll pll 就是每个状态(最大价值和最后一个球的颜色) , v e c t o r < p l l > vector<pll> vector<pll> 其实就是把所有状态存进了一个 v e c t o r vector vector。
这样书写的好处一个是我们可以把每个可能的情况都直接扔进 v e c t o r vector vector 里,而不需要马上讨论更新答案,最后再找 最大价值及颜色和次大价值及颜色。另外一个好处就是我们可以往里面扔两个价值很小且颜色不同的状态来占位置(也就是上面这串代码的 i n f v infv infv),这样就可以不用处理无解或者只有一种颜色的情况——价值小于0就是不符合的情况。
code:
最考C++语法的一集
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#define pll pair<ll,ll>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const int maxk=505;
const ll inf=1e18;
int n,k;
int main(){
cin>>n>>k;
const vector<pll> infv={{-inf,-1},{-inf,-2}};
vector<vector<vector<pll> > > dp(2,vector<vector<pll> >(k+1,infv));
dp[0][0][0].first=dp[0][0][1].first=0;
for(int i=1;i<=n;i++){
ll c,v;
cin>>c>>v;
auto &pre=dp[(i-1)&1],&t=dp[i&1];
for(int j=0;j<=k;j++)t[j]=infv;
for(int j=1;j<=k;j++){//删掉第i个球
for(auto &x:pre[j-1]){
t[j].push_back(x);
}
}
for(int j=0;j<=k;j++){//不删第i个
for(auto &x:pre[j]){
if(x.second!=c){
t[j].push_back(pll(x.first+v,c));
break;
}
}
}
for(int j=0;j<=k;j++){
//排序去重
sort(t[j].begin(),t[j].end(),greater<pll>());
for(int k=1;k<t[j].size();k++){
if(t[j][k].second!=t[j][0].second){
swap(t[j][k],t[j][1]);
break;
}
}
t[j].resize(2);
}
}
ll ans=dp[n&1][k][0].first;
if(ans>=0)cout<<ans<<endl;
else cout<<-1<<endl;
return 0;
}
F - Many Lamps
题意:
有一个简单图,其 N N N 个顶点编号为 1 1 1 到 N N N , M M M 条边编号为 1 1 1 到 M M M 。边 i i i 连接顶点 u i u_i ui 和 v i v_i vi。
每个顶点都有一盏灯。最初,所有的灯都是熄灭的。在 0 0 0 和 M M M 次(包括 0 0 0 次和 M M M 次)之间执行以下操作,确定是否可以正好打开 K K K 盏灯:
- 选择一条边。设 u u u 和 v v v 是边的端点。切换 u u u 和 v v v 上的灯的状态。
也就是说,如果灯亮了,就把它关掉,反之亦然。如果可以准确打开 K K K 盏灯,则打印实现此状态的操作序列。
思路:
直接看 上面说的题解 即可,讲的非常严谨了,没我什么事了。
这里提一嘴链式前向星的一个小性质:加入的第 i i i 条边在 e e e 数组中占第 2 ∗ i − 1 , 2 ∗ i 2*i-1,2*i 2∗i−1,2∗i 的下标,这两条边是正反两个方向的,异或 1 1 1 可以相互切换。
code:
#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
const int maxn=2e5+5;
int n,m,k;
int head[maxn],cnt;
struct edge{
int v,nxt;
}e[maxn<<1];
void add(int u,int v){
e[++cnt].v=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
bool vis[maxn],light[maxn];
int tot=0;
vector<int> ans;
void dfs(int u,int fa){
vis[u]=true;
for(int i=head[u],v;i;i=e[i].nxt){
v=e[i].v;
if(vis[v])continue;
dfs(v,u);
if(!light[v] && tot<k){
light[v]=true;
if(light[u])light[u]=false;
else light[u]=true,tot+=2;
ans.push_back((i+1)>>1);//上面说的链式前向星的存边小性质
}
}
}
int main(){
cin>>n>>m>>k;
if(k&1){
cout<<"No";
return 0;
}
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
add(u,v);
add(v,u);
}
for(int i=1;i<=n;i++)
if(!vis[i])
dfs(i,-1);
if(tot==k){
cout<<"Yes\n"<<ans.size()<<endl;
for(auto x:ans)
cout<<x<<" ";
}
else cout<<"No";
return 0;
}