2. 问题定义

时间序列关系数据（Time Series Relation Data）

这个数据是存放在关系型数据库中，每一条记录都是泰永时间搓的行为。

更具体地，每条记录表示为 $x=(v,t,x_1,x_2,\dots ,x_{m-2})$，其中$v$代表带时间戳的行为，$t$是时间戳，𝑥𝑖代表其他属性，例如设备ID和会话持续时间。

针对时间序列关系数据的欺诈检测（Fraud Detection over Time Series Relation Data）

每一个用户$u\in U$都会有一些列的行为 V = { v 0 , v 1 , … , v n − 1 } V = \{v_0, v_1, \dots, v_{n-1}\} V={v0​,v1​,…,vn−1​}其中$v_i\in V$代表的是用户的行为，$n$是序列的长度。用户的行为数据，也就是$V$通常是按照时间顺序进行呈现的，目的是根据用户的历史顺序行为数据确定用户是否有可以行为，这个任务可以被构建为一个二分类任务。

时间感知行为图

给定一个具有带时间戳的行为序列 V = { v 0 , v 1 , … , v n − 1 } V = \{v_0, v_1, \dots, v_{n-1}\} V={v0​,v1​,…,vn−1​}及相应的属性的用户，其时间感知行为图定义为 G = { V , E , A } G = \{V, E, A\} G={V,E,A}, 其中$V$代表行动节点，$E$是边，$A\in R^{n\ast n}(0\le A_{i,j}\le 1)$是图卷积矩阵（graph convolutional matrix）。图中的每个节点$V_i$代表一条记录，每条边<$v_i,v_j$>的权重与$v_i$代表一条记录，每条边<$v_i$,$v_j$>的权重与 $v_i$和$v_j$之间的时间差成反比。

图卷积矩阵（Graph Convolutional Matrix）

GCN计算所有邻近节点（包含节点本身）的节点特征的胶圈平均值。权重矩阵被称为图卷积矩阵。在时间感知行为图中，构建了一个时间感知的图卷积矩阵来模拟行动之间的相互依赖性。更具体地说，第$i$个节点和第$j$个节点之间的归一化边权重是
$${\tilde{A}}_{i,j}=\frac{{\rho }^{|t_i-t_j|}}{{\sum }_{k=0}^{n-1}{\rho }^{|t_i-t_k|}}$$
,其中$0<\rho <1$ 是控制每个目标节点接受场的范围的超参数。

3. MINT框架

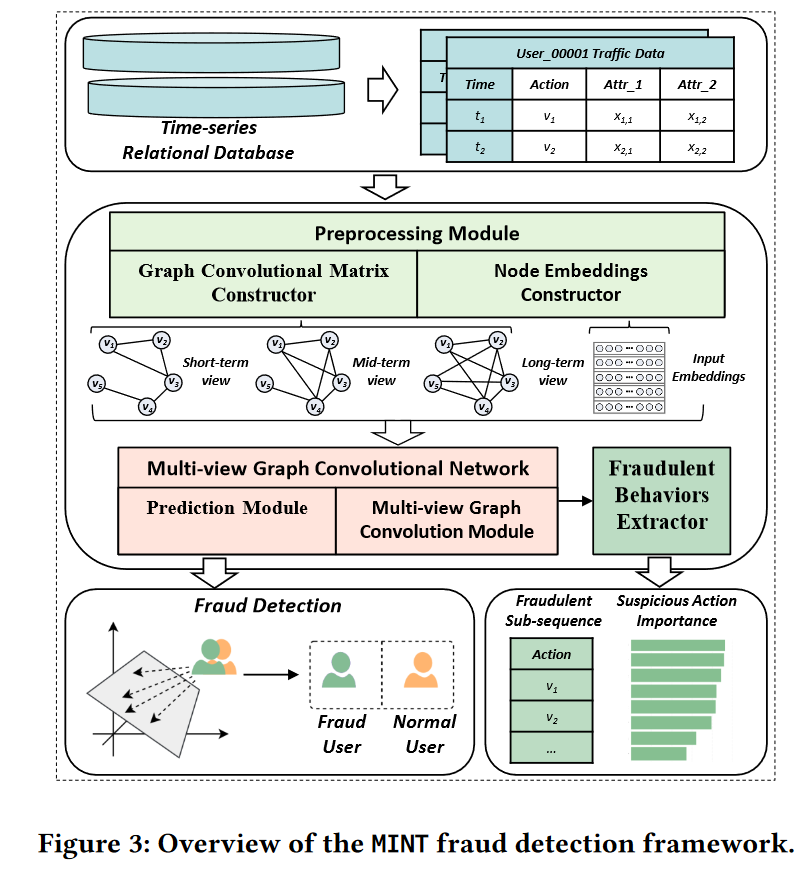
3.1 提取用户的时间信息，构建具有三个不同视角的时间感知行为图。

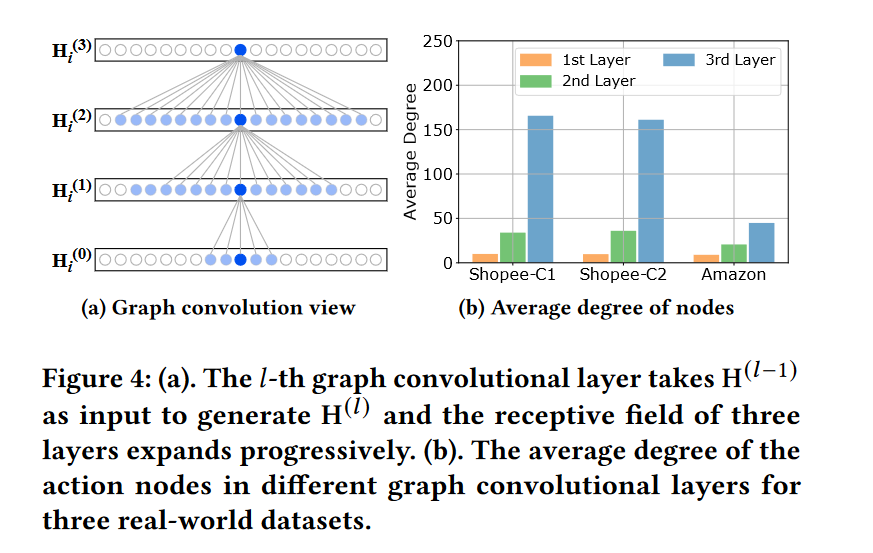
MINT的数据预处理模块由图卷积矩阵构造器和节点嵌入构造器组成。

1. 将每一个行为表示为一个带有相应属性的节点特征
2. 根据算法1构建三个具有不同接收计算的图卷积助阵，这个主要是$\rho$的数值不相同。
3. 更深的图卷积层会聚合更多的邻域信息（图四中的蓝色节点）到目的节点。
4. 每一层中表示的是某一个用户的所有行为，按照的是时间段进行排序，然后，每一个节点的中的属性，例如时间，设备等等，会放入MLP中，输入的维度为$d$，表示的是一个节点（也就是一个行为）的特征。
5. 初始的行为嵌入表示为$H^{(0)}\in R^{n\ast d}$,其中$n$是节点的数量，$d$表示输入嵌入的维度。

3.2 多视图卷积网络

3.2.1 多视图图卷积

在每一层图卷积中，特征聚合如下执行：
$${\mathbf{h}}_{\mathcal{N}(v_i)}^{(l)}=\sum _{v_j\in \mathcal{N}(v_i)}{\mathbf{A}}_{v_i,v_j}^{(l)}\ast {\mathbf{h}}_{v_j}^{(l-1)}$$
我们现在知道，$H^{(0)}=[h_{v_0}^{(0)},h_{v_1}^{(0)},\dots ,h_{v_{n-1}}^{(0)}]$,这个是初始化的特征，通过节点的属性经过$MLP$获取的，

${\mathbf{h}}_{\mathcal{N}(v_i)}^{(l)}$表示的是第$l$层中行动节点$v_i$的聚合邻居表示，${\mathbf{A}}_{v_i,v_j}^{(l)}$表示的是在第$l$层中行动节点$v_j$到节点$v_i$的归一化聚合系数。粗俗一点说也就是第$l$层的节点特征是通过第$l-1$层的节点特征*第$l$层中的图卷积矩阵

然后，对于他自己聚合邻居节点候得特征计算方式如下：
$${\mathbf{h}}_{v_i}^{(l)}=LeakyReLU({\mathbf{W}}^{(l)}{\mathbf{h}}_{\mathcal{N}(v_i)}^{(l)})$$
$LeakyReLU$的激活函数公式如下所示，一般的$ReLU$函数会将小于0的数值变成0，但是$LeakyReLU$会将小于0的数值变成极小值
$$f(x)=\{\begin{array}{llc}x& \mathrm{if}x>0& \\ \alpha x& \mathrm{if}x\le 0& \end{array}$$
可以看见其中的${\mathbf{W}}^{(l)}\in R^{d\ast d}$是第$l$层转换函数中的可训练参数矩阵。

3.2.2 门控邻居交互

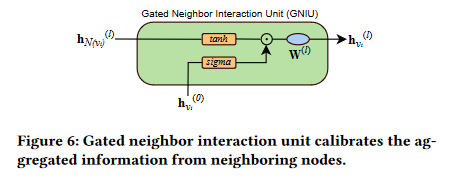
在这一节中，作者推翻了上一小节讲述的东西，现在说的是上一小节的做法会存在过平滑问题。

仅仅依赖时间间隔信息的信息聚合方法会导致严重的过平滑问题。也就是说，一些常见的行为，如‘访问主页’，在用户的行为数据中出现的频率远高于其他行为。导致用户的表示会被常见的行为信息所主导，从而降低欺诈检测的性能。我们将这个问题称为是过平滑问题。为了解决这个问题，我们尝试从邻居节点中尝试去聚合更有用的信息，作者设计了一个门控邻居交互机制。

首先对于第$l$层中行动节点$v_i$的聚合邻居表示${\mathbf{h}}_{\mathcal{N}(v_i)}^{(l)}$，变成了如下公式进行解决：
$${\hat{\mathrm{h}}}_{\mathcal{N}(v_i)}^{(l)}=\text{LayerNorm}(\sigma ({\mathrm{h}}_{v_i}^{(0)})\odot tanh({\mathrm{h}}_{\mathcal{N}(v_i)}^{(l)}))$$
其中，他把初始化的通过节点属性输入进$MLP$中的特征的输出结果，输出进了$\sigma$函数中，其中$\sigma$函数的公式如下：
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
他是把输入的$x$输出为一个[0-1]的数值，这样做的目的可能是引入非线性函数去捕获更加复杂的信息。

然后$tanh(x)$的结构如下所示：
$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
他的输出范围在[-1,1]，通过这样的方式去保持中心化，也可以改善梯度流

采用$LayerNorm$也是为了缓解梯度爆炸或者梯度消失的问题。

最后，在第$l$层中的节点特征${\mathbf{h}}_{v_i}^{(l)}$被表示为：
$${\mathbf{h}}_{v_i}^{(l)}=LeakyReLU({\mathbf{W}}^{(l)}{\hat{\mathbf{h}}}_{\mathcal{N}(v_i)}^{(l)})$$

读出层

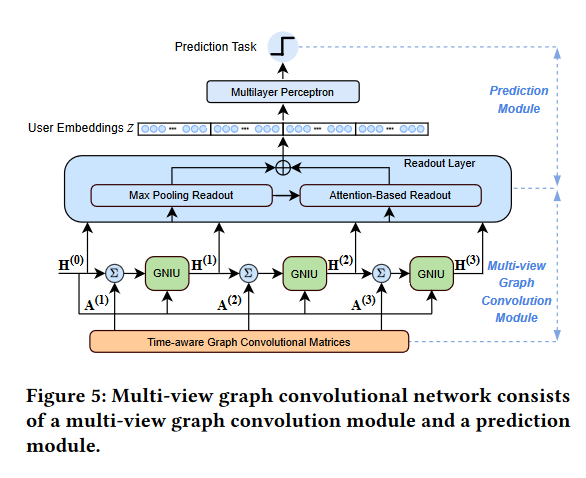
我们为了从行为嵌入矩阵中【$H^{(l)}=[h_{v_0}^{(l)},h_{v_1}^{(l)},\dots ,h_{v_{n-1}}^{(l)}]$,】生成意图嵌入向量，设计了一个最大池化层和基于注意力机制的读出层，如图5所示。我们通过最大池化层去获取最显著的特征，我们称为嵌入相关的意图表示：$h_e^{(0)},h_e^{(1)},h_e^{(2)},h_e^{(3)}$，然后再运用注意力机制去融合在嵌入维度上保持最显著的行为。

对于每个试图，与行为相关的意图表示如下获得：
$${\alpha }^{(l)}={\varphi }_{att}({\mathbf{h}}_e^{(l)},{\mathbf{H}}^{(l)})={\mathbf{h}}_e^{(l{)}^{⊺}}{\mathbf{W}}^{att}{\mathbf{H}}^{(l)}$$
${\mathbf{h}}_e^{(l{)}^{⊺}}\in R^{d\ast n}$|${\mathbf{W}}^{att}\in R^{d\ast d}$|$H^{(l)}\in R^{n\ast d}$ => ${\alpha }^{(l)}\in R^{n\ast n}$

注意力机制计算后的结果：
$${\mathbf{h}}_a^{(l)}=\sum _{i=0}^{n-1}{\alpha }_i^{(l)}\cdot {\mathbf{h}}_i^{(l)},{\alpha }_i^{(l)}\in {\mathbf{\alpha }}^{(l)},{\mathbf{h}}_i^{(l)}\in {\mathbf{H}}^{(l)}$$
${\alpha }^{(l)}\in R^{n\ast n}$|${\mathbf{h}}^{(l)}\in R^{n\ast d}$ => ${\mathbf{h}}_a^{(l)}\in R^{n\ast d}$

最后，该层的每个节点特征为：${\mathbf{h}}^{(l)}={\mathbf{h}}_e^{(l)}+{\mathbf{h}}_a^{(l)}.$ 最后${\mathbf{h}}^{(l)}\in R^{n\ast d}$

3.2.3 预测模块 (Prediction Module)

$$\begin{array}{rl}\mathbf{z}& =CONCATE([{\mathbf{h}}^{(0)},{\mathbf{h}}^{(1)},{\mathbf{h}}^{(2)},{\mathbf{h}}^{(3)}])\\ & \\ p& ={\varphi }_{MLP}(z),{\varphi }_{MLP}:{\mathbb{R}}^{4\ast d}\mapsto \mathbb{R}\end{array}$$